
经的 §8-1 复数 二、复数运算 乘法:模相乘, 角相加。 (2)乘除运算(利用极坐标) AB=ABLφa+pb A= A B= 0b号 A A 0a -Pb B 说明: AB (ar jaz)(bi jb2)(aibi-azb2)j(aib2 azb) A ar jaz =1 bab azbi aib2 B bi jb2 br2+b2 br2+b22
现代制造装备工程技术开发中心 佛山科学技术学院 二、复数运算 (2)乘除运算(利用极坐标) a b a b a b AB = A B φ + φ A = A φ B = B φ A A = φ - φ B B §8-1 复数 乘法:模相乘, 角相加。 除法:模相除, 角相减。 说明: 2 2 2 1 2 1 2 1 1 2 2 1 2 2 1 1 2 1 1 2 2 2 1 1 2 2 1 2 1 2 1 2 AB = (a + ja )(b + jb ) = (a b - a b ) + j(a b + a b ) A a + ja a b + a b a b - a b = = + j B b + jb b + b b + b
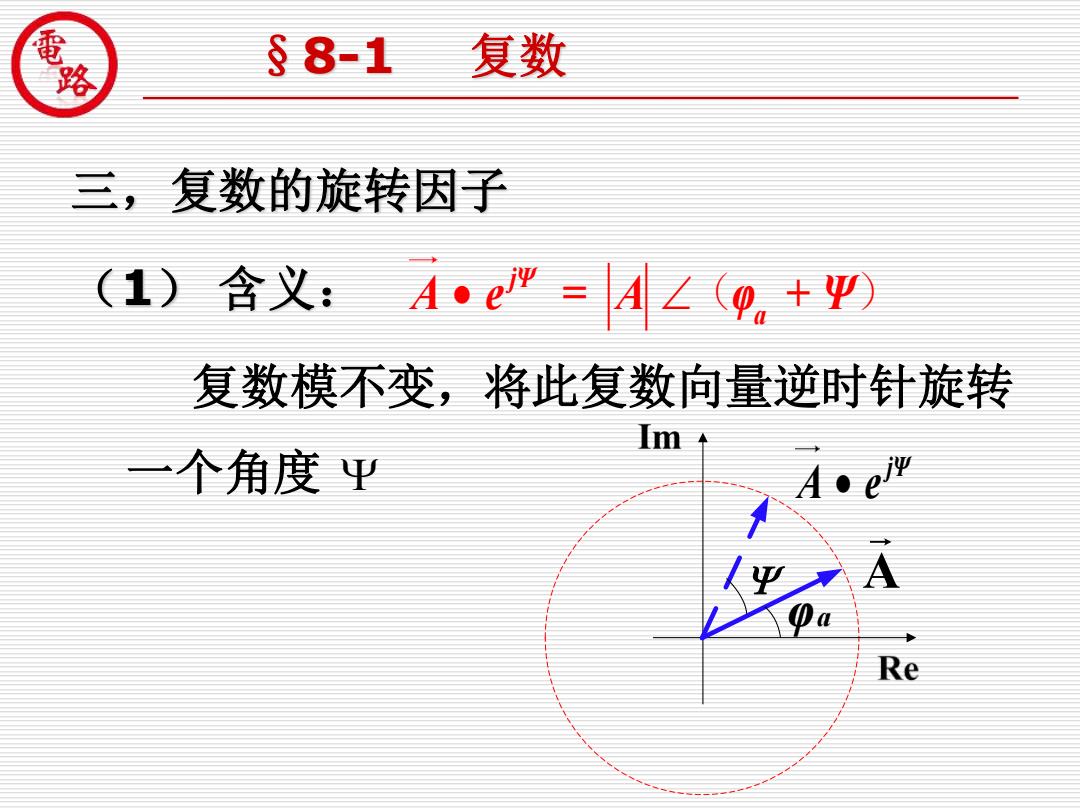
经的 §8-1 复数 三,复数的旋转因子 (1)含义:A·e" AL(0. +Ψ) 复数模不变,将此复数向量逆时针旋转 m 一个角度Ψ A·e Re
现代制造装备工程技术开发中心 佛山科学技术学院 三,复数的旋转因子 (1) 含义: 复数模不变,将此复数向量逆时针旋转 一个角度 §8-1 复数 A e = A • jΨ (φa + Ψ) • jΨ A e φa A
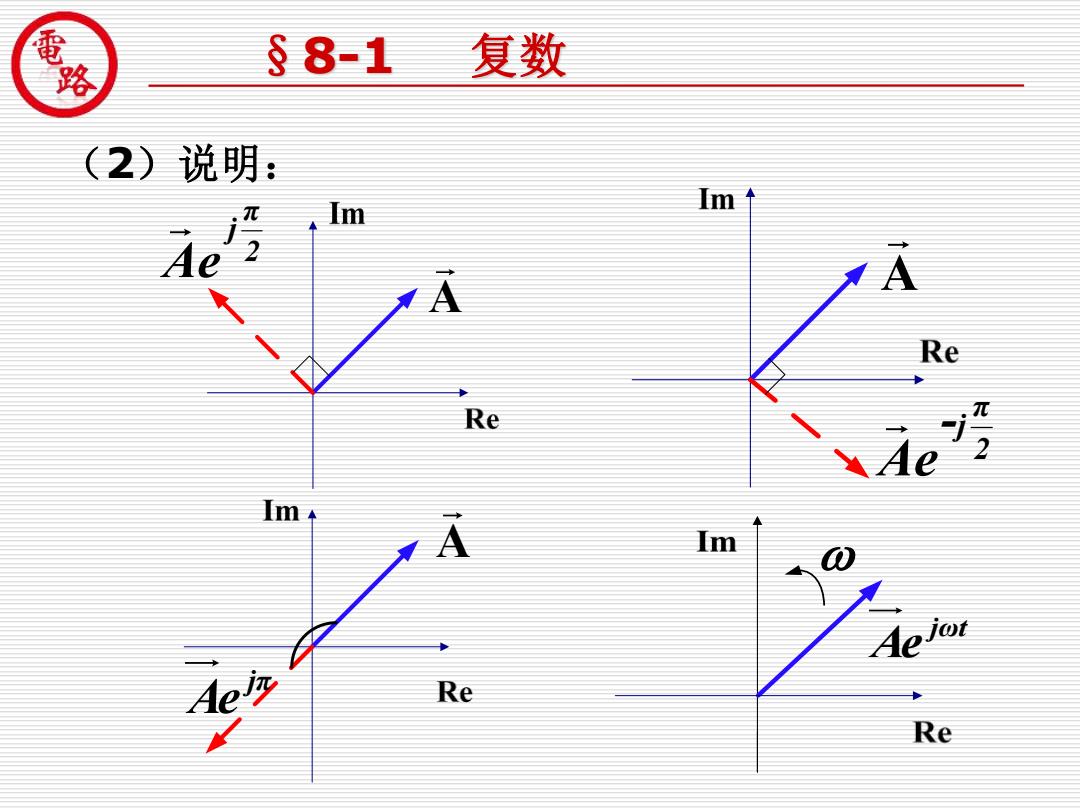
经效 §8-1 复数 (2)说明: .1m m A Re Re 2 Im m Re Re
现代制造装备工程技术开发中心 佛山科学技术学院 (2)说明: §8-1 复数 A π j Ae 2 jπ Ae A jωt Ae A π j 2 - Ae

的 第八章相量法 §8-2 正弦量 、 正弦稳态电路 1、正弦稳态电路:线性电路在正弦激励下稳 定时的电路 2、正弦稳态电路特点:若激励均为同一频率 正弦函数,则此电路中全部响应〈、)均为 同一频率的正弦函数 3、应用:电力工程中所用电源以及所产生、4 均为正弦函数;非正弦周期函数可以分解成正 弦函数
现代制造装备工程技术开发中心 佛山科学技术学院 §8-2 正弦量 一、正弦稳态电路 1、正弦稳态电路:线性电路在正弦激励下稳 定时的电路 2、正弦稳态电路特点:若激励均为同一频率 正弦函数,则此电路中全部响应〈 、 〉均为 同一频率的正弦函数 3、应用:电力工程中所用电源以及所产生 、 均为正弦函数;非正弦周期函数可以分解成正 弦函数 第八章 相量法

经的 §8-2 正弦量 二、正弦、W(以正弦为例) 1、正弦:一种特殊的、周期的、交变的电流 2、正弦表示方法: (1)数学式:i=I,mc0s(ωt+p) 说明:*Im一一正弦电流的最大值,振幅 *ω一一角频率(反映正弦量变化快慢) *T一一周期 一一频率 01
现代制造装备工程技术开发中心 佛山科学技术学院 2、正弦 表示方法: (1)数学式: 说明: ——正弦电流的最大值,振幅 ——角频率(反映正弦量变化快慢) ——周期 ——频率 §8-2 正弦量 二、正弦 、 (以正弦 为例) 1、正弦 :一种特殊的、周期的、交变的电流 m i i = I cos(ωt + φ )