
经的 第八章相量法 正弦i、u 本章内容 正弦i、u的相量表示法、相量法 KCL、KVL的相量形式 §81 复数 §8-2 正弦量 §83 相量法的基础 §8-4 电路定律的相量形式
现代制造装备工程技术开发中心 佛山科学技术学院 第八章 相量法 正弦i、u 本章内容 正弦i、u的相量表示法、相量法 KCL、KVL的相量形式 §8-1 复数 §8-2 正弦量 §8-3 相量法的基础 §8-4 电路定律的相量形式

经的 §8-1 复数 复数表示方法: (1)直角坐标形式: A=a+jb 说明: a=ReA 实部 Im b=mA虚部 j不用,j=√1 A可在复平面画出 Re
现代制造装备工程技术开发中心 佛山科学技术学院 一、复数表示方法: (1)直角坐标形式: 说明: 实部 虚部 可在复平面画出 A = a + jb a = Re A b = Im A A §8-1 复数 j 不用 i, j = −1 ...... ...... a b A
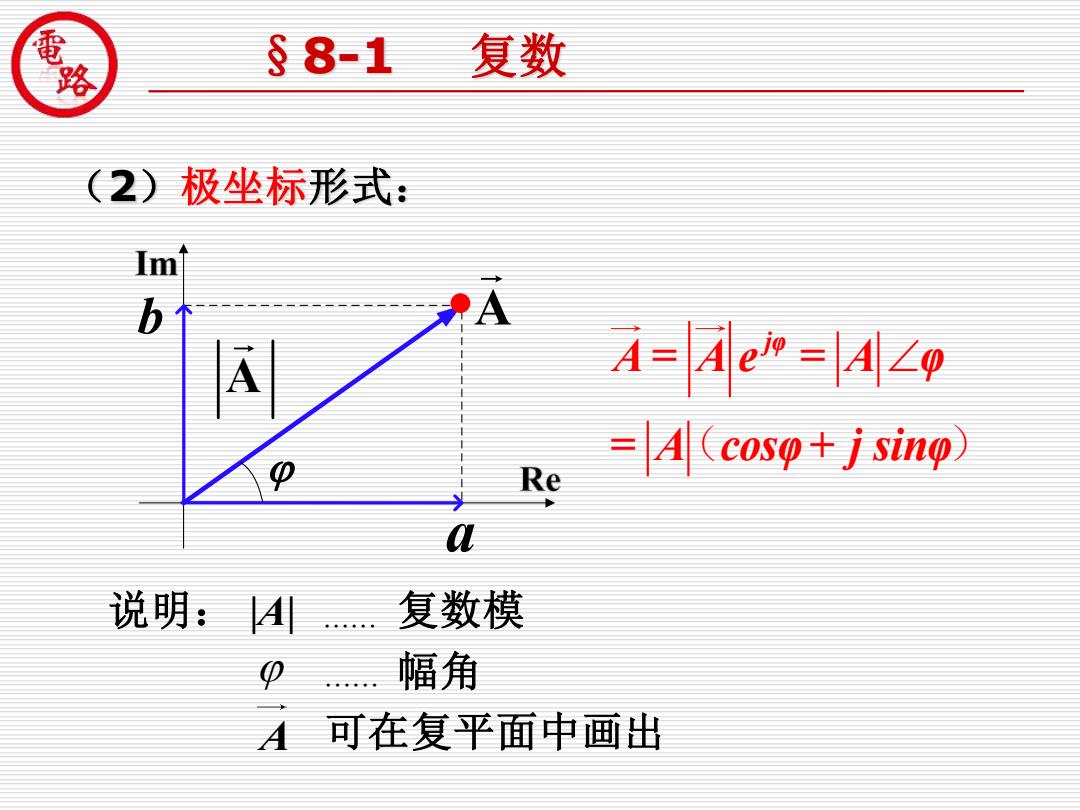
的 §8-1 复数 (2)极坐标形式 Im b i=Aem =29 Re =A (coso+jsing a 说明:A 复数模 幅角 A 可在复平面中画出
现代制造装备工程技术开发中心 佛山科学技术学院 (2)极坐标形式: 说明: |A| 复数模 幅角 可在复平面中画出 ( ) jφ A = A e = A φ = A cosφ+ j sinφ A §8-1 复数 a b A A ......

悠的 §8-1 复数 (3)直角坐标和极坐标间转换 A=a+jb=√+b∠tan A=A Acoso jsing 例:A=1+j=V2L4药 A=√2Z30=√2co30+jN2im30
现代制造装备工程技术开发中心 佛山科学技术学院 (3)直角坐标和极坐标间转换 例: 2 2 -1 a A = a + jb = a + b tan b A = A φ = A cosφ + j A sinφ A = 1 + j = 2 45 A = 2 30 = 2cos30 + j 2sin30 §8-1 复数

经的 §8-1 复数 二、复数运算 (1)加减运算(利用直角坐标形式) 若:A=u1士jb1,A2=2jb2 m A+A2 则:A1士A2(a1士2)Hj(b1±b2) 加减法可用图解法 Re ArA2
现代制造装备工程技术开发中心 佛山科学技术学院 二、复数运算 (1)加减运算(利用直角坐标形式) 若: A1 =a1+jb1, A2 =a2+jb2 则:A1±A2=(a1±a2 )+j(b1±b2 ) 加减法可用图解法 §8-1 复数