
3、调制特性 DFS[W(n]=X(k+1) W-1 证:DFS[Wx(n】=∑W(n)W n=0 N-1 -∑0n)WWa n=0 =(k+)
3、调制特性 [ ( )] ( ) nl DFS W x n X k l N 1 0 [ ( )] ( ) N ln ln nk N N N n DFS W x n W x n W 证: 1 ( ) 0 ( ) N l k n N n x n W X k l ( )

4、周期卷积和 若(K)=文(K)·永2(k) 则m=DFS(k】=∑x(m)x,(n-m) m=0 N- =∑,(m)元,(n-m) m=0
4、周期卷积和 1 2 1 0 ( ) ( ) N m x m x n m 1 2 若 Y k X k X k ( ) ( ) ( ) 1 1 2 0 ( ) [ ( )] ( ) ( ) N m y n IDFS Y k x m x n m 则
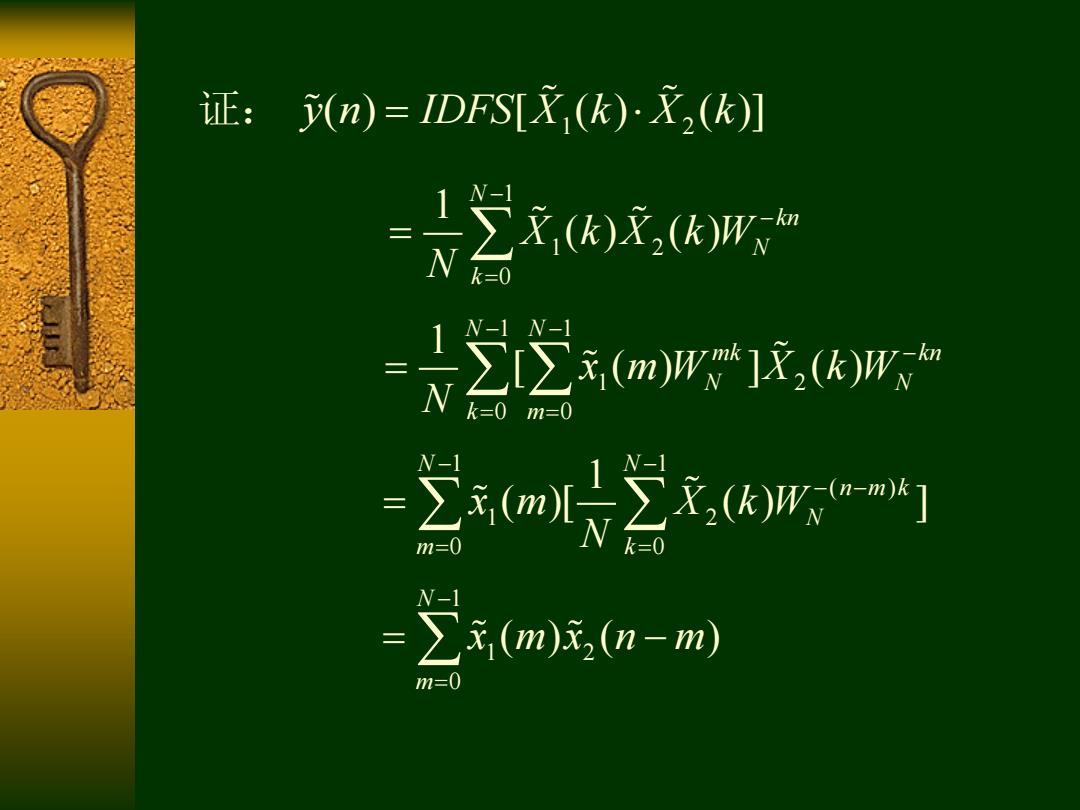
证:(n)=IDFSIX(K)文2(k)] 2,w k=0 -22mr1R传男 k=0m=0 m(1 m=( =∑x(m)元2(n-m) m=0
1 2 证: y n IDFS X k X k ( ) [ ( ) ( )] 1 1 2 0 1 ( ) ( ) N kn N k X k X k W N 1 1 1 2 0 0 1 [ ( ) ] ( ) N N mk kn N N k m x m W X k W N 1 1 ( ) 1 2 0 0 1 ( )[ ( ) ] N N n m k N m k x m X k W N 1 1 2 0 ( ) ( ) N m x m x n m

(m) L.,m 1012N-1N ( 1012 (-m) 1012 (1-m) 01 2-m) 012 Xi(mX(2-m) ↓012 !N 1012

例:已知序列x(n)=R(n),x2(n)=(n+1)R(n) 分别将序列以周期为6周期延拓成周期序列 ,(n)和2(n),求两个周期序列的周期卷积和。 V- 解:m)=∑x(m),(n-m m=0 =∑元(m)元,(n-m) m=0
1 4 2 5 1 2 ( ) ( ) ( ) ( 1) ( ) 6 ( ) ( ) x n R n x n n R n x n x n 例:已知序列 , 分别将序列以周期为 周期延拓成周期序列 和 ,求两个周期序列的周期卷积和。 1 1 2 0 ( ) ( ) ( ) N m y n x m x n m 解: 5 1 2 0 ( ) ( ) m x m x n m