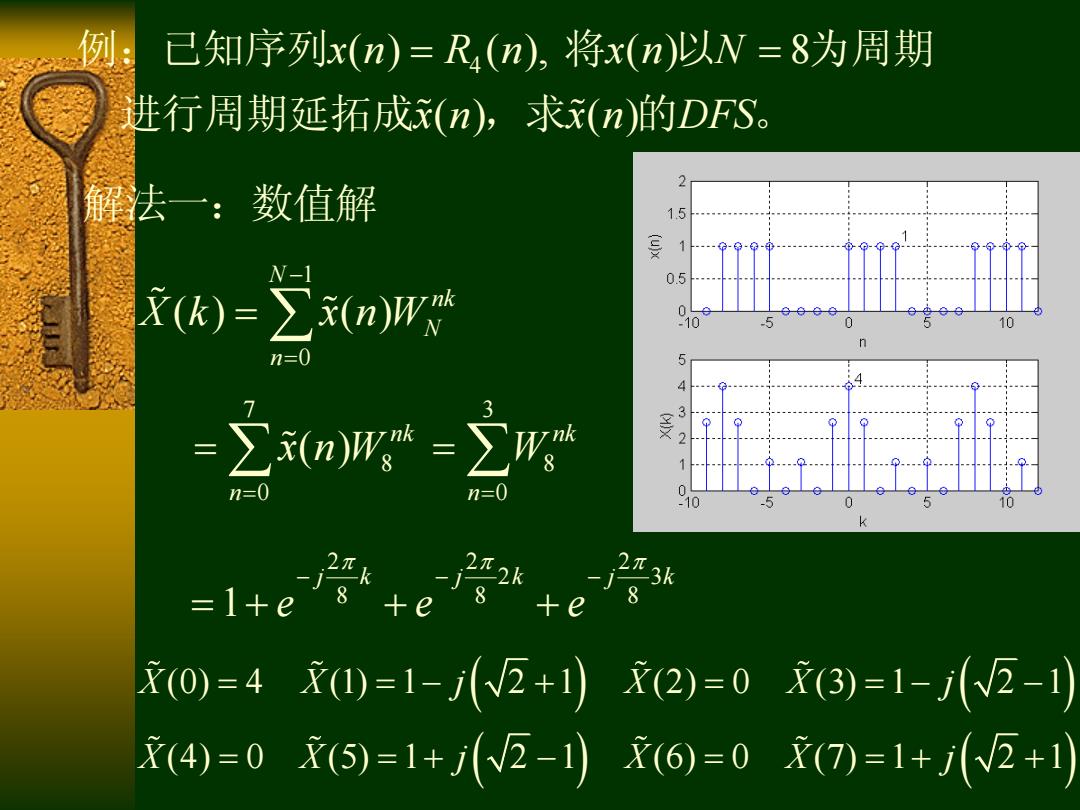
已知序列x(n)=R(n),将x(n)以N=8为周期 进行周期延拓成x(n),求x(n)的DFS。 2 解法一:数值解 1.5 W-1 0.5 )=Σn)w eeee 10 5 0 n=0 5 4 -∑0mm*-∑H 3 2 1 =1+e+e+ 2元3k 0)=4四=1-(2+)2)=0(3)=1-(W2-) (4)=0x(5)=1+(2-)(6)=0()=1+(2+1)
4 ( ) ( ), ( ) 8 ( ) ( ) x n R n x n N x n x n DFS 例:已知序列 将 以 为周期 进行周期延拓成 ,求 的 。 解法一:数值解1 0 ( ) ( ) N nk N n X k x n W 7 8 0 ( ) nk n x n W 2 2 2 2 3 8 8 8 1 j k j k j k e e e 3 8 0 nk n W (0) 4 (1) 1 2 1 (2) 0 (3) 1 2 1 (4) 0 (5) 1 2 1 (6) 0 (7) 1 2 1 X X j X X j X X j X X j
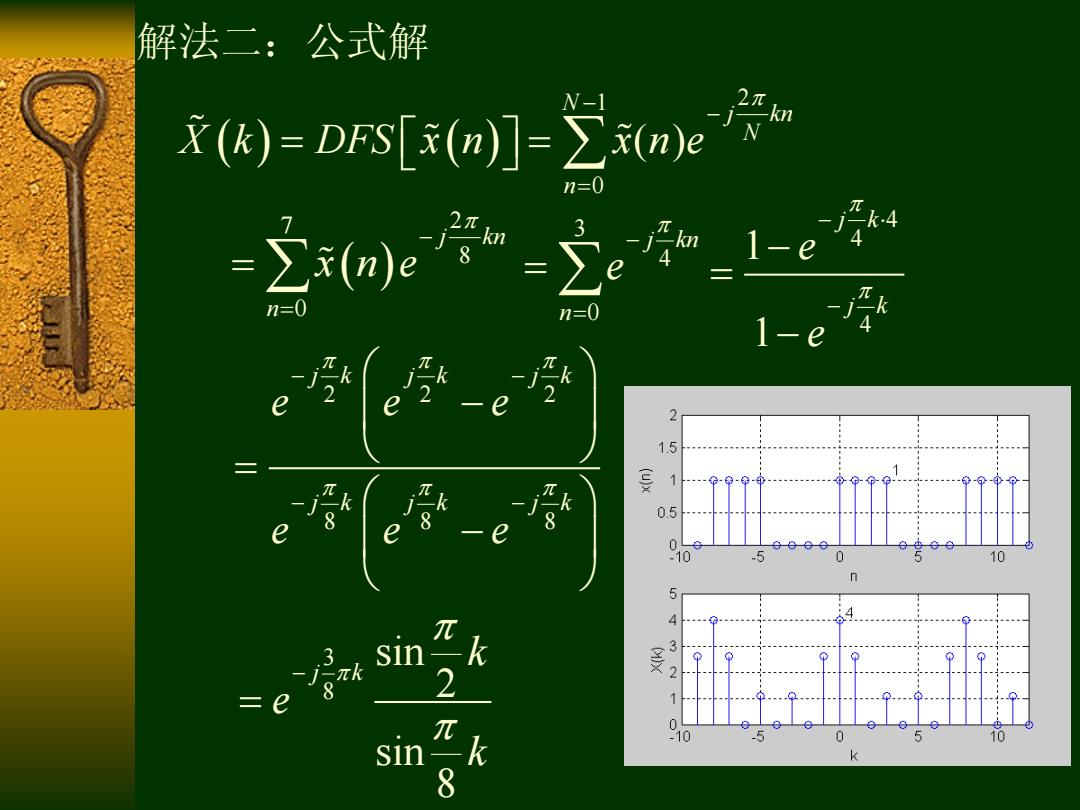
解法二:公式解 ()=DFs[x(a]-∑ne n=0 k.4 -2oe-2- 1-e n=0 n=0 1-e e 2 1.5 复 0.5 e 8 8 0 -10 -5 0 5 10 5 4 A sin k 3 分 2 2 =e π sin k -10 8
1 2 0 ( ) N j kn N n X k DFS x n x n e 解法二:公式解 7 2 8 0 j kn n x n e 3 4 0 j kn n e 2 2 2 8 8 8 j k j k j k j k j k j k e e e e e e 4 4 4 1 1 j k j k e e 3 8 sin 2 sin 8 j k k e k

X(k)与z变换的关系: 0≤n≤N-1 其它n 对x(m)作z变换:X()=∑x(n)”-∑x(n):” n=-00 n=0 ()=∑(n)W=X(e儿,为 n=0 .(k)可看作是对(n)的 jIm 一个周期x(n)做z变换 1z=1 然后将2变换在2平面 2π k=0 Re 单位圆上按等间隔角 N 7(k=N-1) 抽样得到
X k z 与 变换的关系: 0 1 0 x n n N x n n 令 其它 对 作 变换: x n z 1 0 N n n n n X z x n z x n z 2 1 0 j k k N N N nk N z W e n X k x n W X z 可看作是对 的 一个周期 做 变换 然后将 变换在 平面 单位圆上按等间隔角 抽样得到 X k x n x n z z 2 N z

DFS的性质 1、线性: 若 文,(k)=DFST,(n] X,(k)=DFS[(n)] 则 DFS[a(n)+b成,(n]=a,(k)+br2(k) 其中,a,b为任意常数
DFS的性质 1、线性: 其中, a b, 为任意常数 1 1 X k DFS x n ( ) [ ( )] 2 2 X k DFS x n ( ) [ ( )] 若 1 2 1 2 DFS ax n bx n aX k bX k [ ( ) ( )] ( ) ( ) 则

2、序列的移位 DSTn+m】=联X)=e节x0] 证:DFS[(n+m】=∑(n+m)W n=0 N-1+m 令i=n+m =∑(0W-) i=m N-1 =W∑()W=Wv*X(k) i=0
2、序列的移位 2 [ ( )] ( ) ( ) j mk mk N DFS x n m W X k e X k N 1 0 [ ( )] ( ) N nk N n DFS x n m x n m W 证: 1 ( ) ( ) N m k i m N i m x i W 令i n m 1 0 ( ) ( ) N mk ki mk N N N i W x i W W X k