第3章波函数与格林國数 高等电赋场望论 N 0.4 N2 0.2 2 4 6 10 1.0 0.2 -0.4 0.6 J2 02 第二类BesselE函数 0 2 4 10 x -0.2 第一类Besselp函数
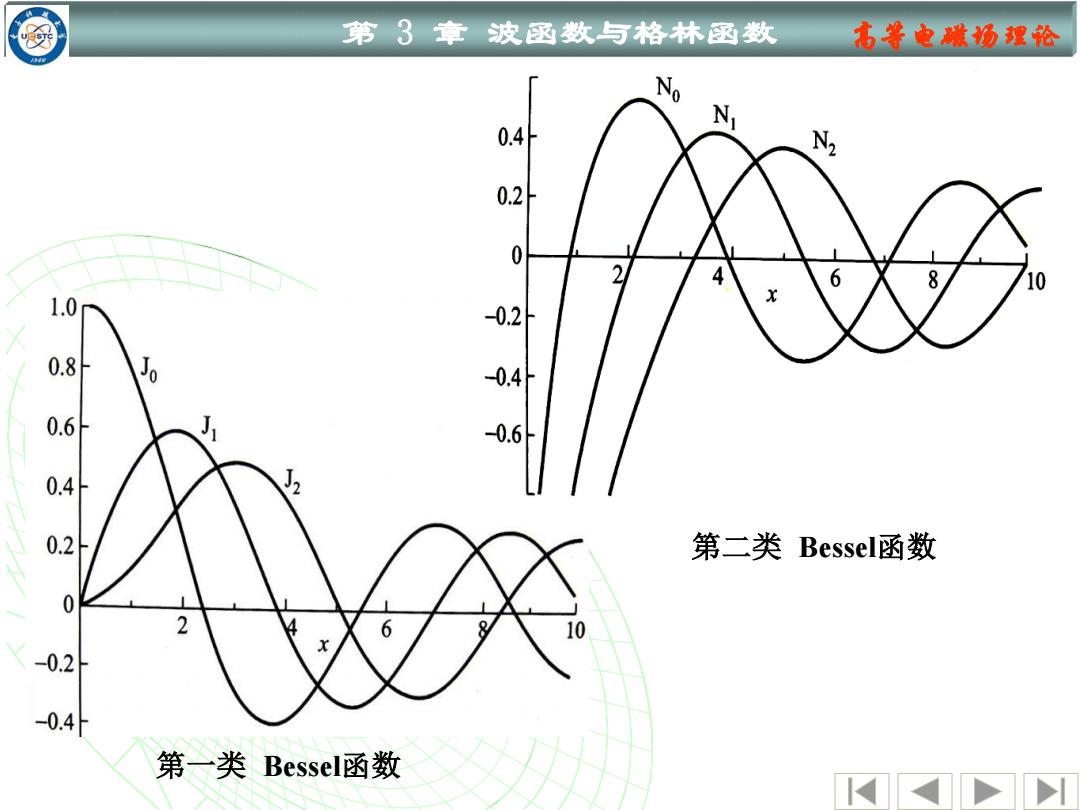
第 3 章 波函数与格林函数 高等电磁场理论 第一类 Bessel函数 第二类 Bessel函数

第3章波函数与格林函数 右等电微场理论 ★圆柱函数的渐近公式 ① u-→0 J(u)→1 J.=学r≥ 2n2 No(u)- N.w.a学m2 ro0-2n号 Hw)“》(学m≥ 元 ow)-/会吗 0-"元”学”m≥训
第 3 章 波函数与格林函数 高等电磁场理论 (1) 0 2 ( ) ln 2 u H u j 0 J u( ) 1 → 0 2 ( ) ln 2 u N u ( 1)! ( ) ( ) 2 n n n u N u − − (1) ( 1)! ( ) ( ) 2 n n n u H u j − − (2) 0 2 ( ) ln π 2 u H u j − (2) ( 1)! ( ) ( ) 2 n n n u H u j − − − ( 1) n ( 1) n ( 1) n ★ 圆柱函数的渐近公式 ① u → 0 1 ( ) ( ) ! 2 n n u J u n = ( 1) n

第3章波函数与格林函数 右等电微场理论 ② L→o∞ J(0→ πu 驻波解 N,(u)→ 2 πl 行波解 H2(W→ 2-j(w-v24 πW
第 3 章 波函数与格林函数 高等电磁场理论 ( ) (1) 2 4 2 ( ) e j u H u v u − − → ( ) (2) 2 4 2 ( ) e j u H u v u − − − → —— 行波解 2 ( ) cos( ) 2 4 J u u u → − − 2 ( ) sin( ) 2 4 N u u u → − − —— 驻波解 ② u →

第3章波函数与格林函数 名等电微场望论 ★贝塞尔函数的母函数 e-2=∑t”Jn(x) n=-o 令t=-jet,x=kp→kpcos=∑(-j)rn(kp)em 平面波函数 柱面波函数 令t=-jej,x=kp→kpeosd=∑(-j)”Jn(kp)eJw 1=-oG 令t=je,x=kp→enos=∑jJn(kp)ew 令t=el,x=kp一ejkpsing0 = ∑Jn(kp)eiw n=-00
第 3 章 波函数与格林函数 高等电磁场理论 ★ 贝塞尔函数的母函数 ( 1/ ) / 2 e ( ) x t t n n n t J x − =− = j t x k e , 令 = = j sin j e ( )e k n n n J k =− = j cos j e ( j) ( )e k n n n n J k − =− = − j t x k je , 令 = − = j cos j e ( j) ( )e k n n n n J k − − =− = − j t x k je , − 令 = − = j cos j e j ( )e k n n n n J k =− = j t x k je , 令 = = 平面波函数 柱面波函数

第3章波函数与格林函数 右等电微场理论 ★贝塞尔函数的积分表示 ersn=∑Jn(x)e n=-o∞ →.6)-271eona-27」cs-w0 ●● e-jxcos (-,es1).eo0 n=-00 cos=】 em-2e6
第 3 章 波函数与格林函数 高等电磁场理论 ★ 贝塞尔函数的积分表示 j sin j e ( )e x n n n J x =− = 1 j( sin ) ( ) e d 2 x n n J x − − = 1 cos( sin )d 2 x n − = − cos j e ( j) ( )e jx n n n n J x − =− = − j cos j e j ( )e x n n n n J x =− = j( cos ) j ( ) e d 2 n x n n J x − + − = j( cos ) ( j) ( ) e d 2 n x n n J x − − − =