
第3章波函数与格林函数 名等电微场望论 ★贝塞尔函数的正交性 (k.(do- 0 i≠ g引°+1} 其中kp是Jn(koa)=0或J,(k,a)=0的第i个根 ★傅里叶一一贝塞尔级数 F(p)=∑a,Jn(kp) (0≤p≤a) i=1 a三 .(k(dp
第 3 章 波函数与格林函数 高等电磁场理论 ★ 贝塞尔函数的正交性 2 0 0 ( ) ( )d a n i n j i i j J k J k Q i j = = i k ( ) 0 n J k a = ( ) 0 n J k a 其中 是 或 = 的第i 个根 1 ( ) ( ) i n i i F a J k = = 2 0 1 ( ) ( )d a i n i i a J k F Q = (0 ) a ★ 傅里叶——贝塞尔级数

第3章波函数与格林函数 右等电微场望论 1、有界空间的一般解(k。k取离散值) w(.)=>CmB.(komp)h(v)h(km=) m.v 例:圆柱形波导(p<a)中的标量波函数 圆柱形波导 incn 基本标量波函数 cos(nφ) e±km e”一偶模; “0”一奇模。 一般解(p,,)=∑∑Ann6mg(p,0,) m=1n=0 或基本标量波函数 Vmn(p)=Jn(komp)etme 般解w(p,中,2)=∑∑Arn Vmn(p,中,z) m=1n=-∞
第 3 章 波函数与格林函数 高等电磁场理论 1、 有界空间的一般解 k ( 、 k z 取离散值) , ( , , ) ( ) ( ) ( ) m m zm m z C B k h h k z = cos( ) ( , , ) ( ) e sin( ) jk z zm m n e n m o n z J k n = 例:圆柱形波导 ( ) a 中的标量波函数 “ ” e —— 偶模; “ ” o —— 奇模。 圆柱形波导 y x z O a • 一般解 1 0 ( , , ) ( , , ) mn mn m n e e o o z A z = = = • 基本标量波函数 ( , , ) ( )e e jn jk z zm mn n m z J k = • 一般解 1 ( , , ) ( , , ) mn mn m n z A z = =− = 或 基本标量波函数
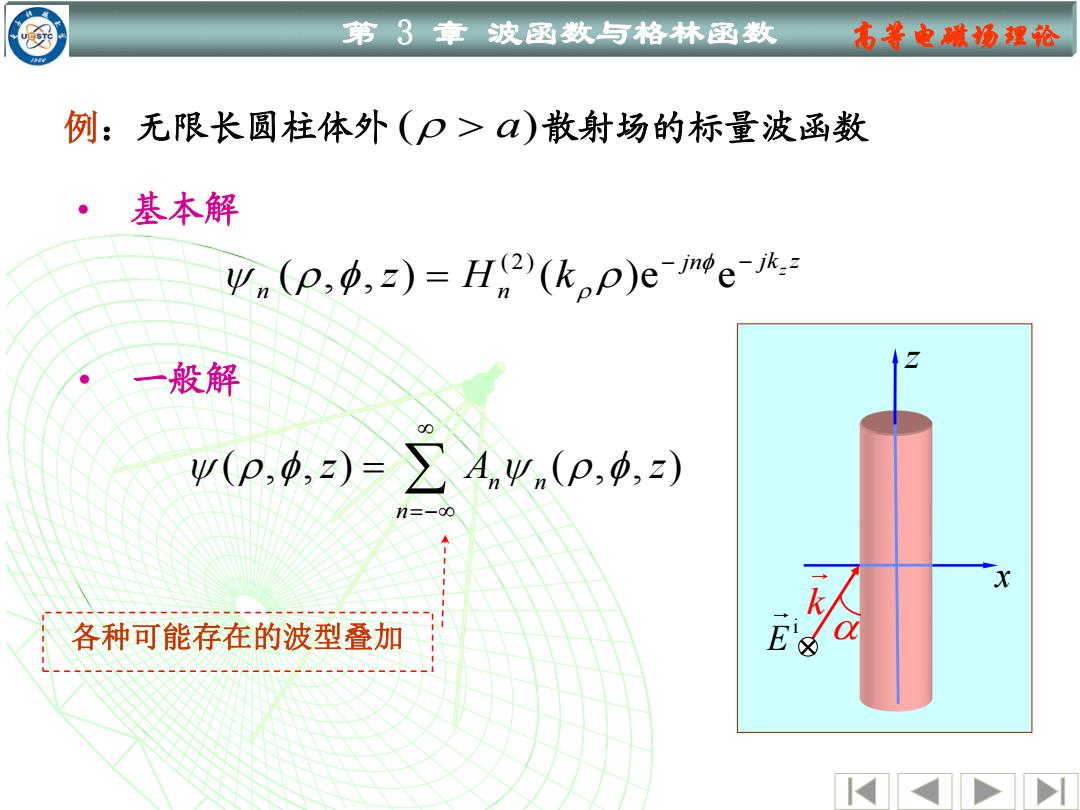
第3章波函数与格林函数 右等电微场理论 例:无限长圆柱体外(p>)散射场的标量波函数 ·基本解 (p)=H(kp)e-me 般解 W(p.0,z)= ∑Anwn(p,p,z) n=-0o 各种可能存在的波型叠加 &☒
第 3 章 波函数与格林函数 高等电磁场理论 (2) ( , , ) ( )e e z jn jk z n n z H k − − = 例:无限长圆柱体外 ( ) a 散射场的标量波函数 x z a i E k • 一般解 ( , , ) ( , , ) n n n z A z =− = 各种可能存在的波型叠加 • 基本解
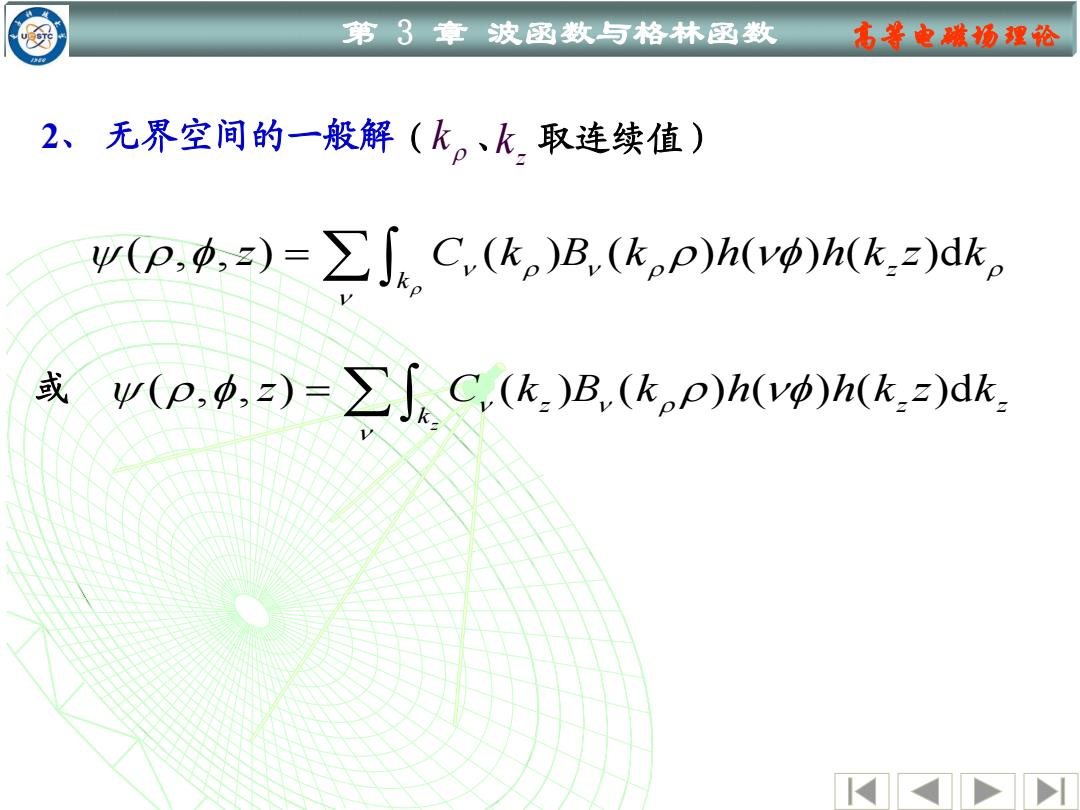
第3章波函数与格林函数 右等电微场理论 2、无界空间的一般解(k。、k.取连续值) w(p,4,2)=∑JC,(k)B,(k,P)hw)hk)dk。 或(p,,z)=∑∫人C,(k)B(kp)h()h(k2)dk
第 3 章 波函数与格林函数 高等电磁场理论 2、 无界空间的一般解 k ( 、 k z 取连续值) ( , , ) ( ) ( ) ( ) ( )d z k z C k B k h h k z k = 或 ( , , ) ( ) ( ) ( ) ( )d z z z z k z C k B k h h k z k =

第3章波函数与格林函数 名等电微场望论 3.1.3 球面波函数yw(r,B,0) 方程 (sin0 1+k=0 or 60 r2sin20 002 基本解w(r,B,)=R(r)T(Θ)Φ() 则 dΦ +v2Φ=0→Φ()=h(vφ) 在周期性条件下,V=n 2 n du du 连带勒让德方程 d (2 dr 迟)+k,2-(n+]R=0一球贝塞尔方程 dr
第 3 章 波函数与格林函数 高等电磁场理论 2 2 2 2 2 2 2 2 1 1 1 ( ) (sin 0 sin sin r k r r r r r + + + = 方程 ) 基本解 ( , , ) ( ) ( ) ( ) r R r T = 3.1.3 球面波函数 ( , , ) r 则 2 2 2 d 0 d + = 在周期性条件下, = m ( ) ( ) = h 2 2 2 ——球贝塞尔方程 d d ( ) [ ( 1)] 0 d d R r k r n n R r r + − + = 2 2 2 d d [(1 ) ] [ ( 1) ] 0 d d 1 T m u n n T u u u − + + − = − ( cos ) u = 奇点: 0 0, r = = ——连带勒让德方程