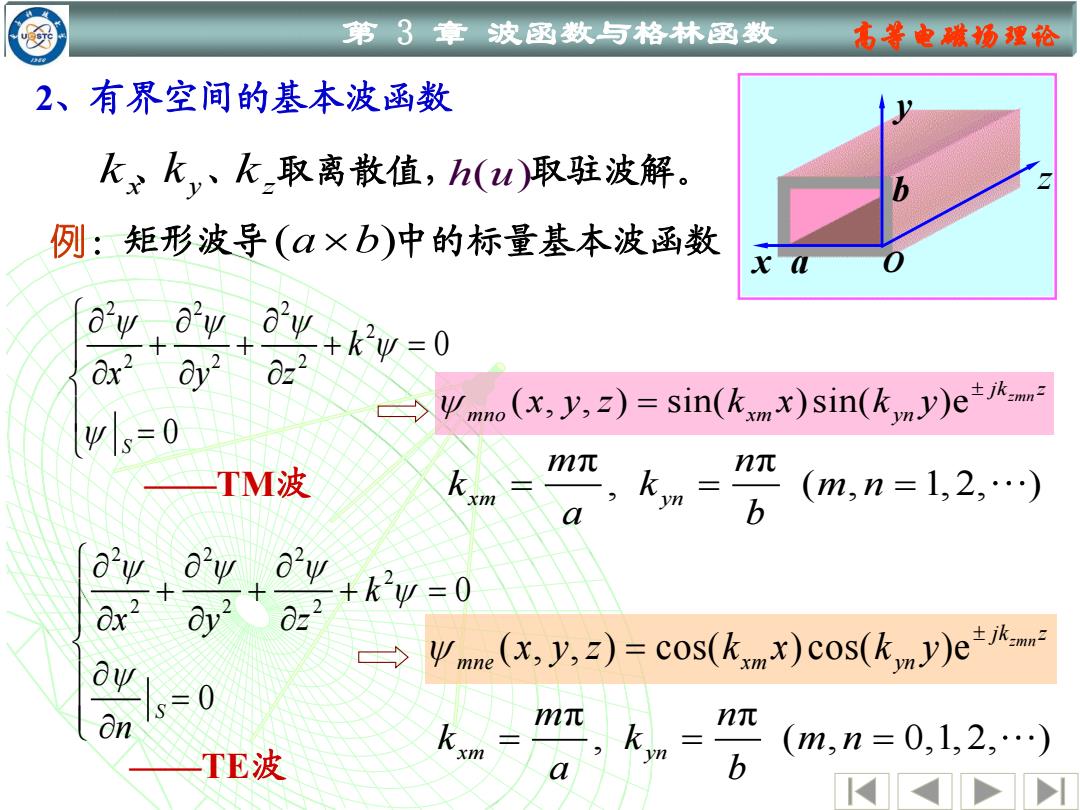
第3章波函数与格林函数 名等电微场理论 2、有界空间的基本波函数 飞x飞y、k取离散值,h(u)取驻波解。 例:矩形波导(α×b)中的标量基本波函数 x a 8'w a'w Ox2 y2 oW+kw-O 0z2 Ψmo(x,y,z)=sin(kmx)sin(kmy)e±.m Ψs=0 m元 元 TM波 三 =b (m,n=1,2,…) 8'w 6 Ox2 0z2 →Ψme(x,y,z)=cos(krmx)cos(k,my)eJka s=0 On m元 n元 Kxm 个三 (m,n=0,1,2,…) TE波 a
第 3 章 波函数与格林函数 高等电磁场理论 2、有界空间的基本波函数 h u( ) x k 、 k y 、 k z 取离散值, 取驻波解。 例:矩形波导 ( ) a b 中的标量基本波函数 x y z O b a 222 2 2 2 2 0 0 S k x y z + + + = = 222 2 2 2 2 0 0 S k x y z n + + + = = ( , , ) sin( ) sin( )e zmn jk z mno xm yn x y z k x k y = π π , ( , 1, 2, ) xm yn m n k k m n a b = = = ( , , ) cos( ) cos( )e zmn jk z mne xm yn x y z k x k y = π π , ( , 0,1, 2, ) xm yn m n k k m n a b = = = ——TE波 ——TM波

第3章波函数与格林函数 右等电微场理论 正交性 v. m'≠m,orn≠n ab/4,m'=m,and n'=n 0, m'≠,orn'≠n ab/2,m'=m=0,and n'=n+0 mme(xy,(x,y,dxdy= ab/2,m'=m≠0,andn'=n=0 ab/4,m'=m≠0,andn'=n≠0 v(.y.-)vi.(x.y.ayaxdy-0 me(x,y,W(xy,=dxdy=0 般解 (x,y,2)=∑Am84mmg(x,y2) m.n 各种可能存在的波型叠加
第 3 章 波函数与格林函数 高等电磁场理论 • 一般解 , ( , , ) ( , , ) mn mn m n e e o o x y z A x y z = • 正交性 各种可能存在的波型叠加 0 0 0, , ( , , ) ( , , )d d / 4, , and a b mno m n o m m n n x y z x y z x y ab m m o n n r = = = 0 0 0, , / 2, 0 and and a , 0 ( , , ) ( , , )d d / 2, 0, 0 / 4, 0, n d 0 a b mne m n e m m n n ab m m n n x y z x y z x y ab m m n n ab m m r n n o = = = = = = = = = 0 0 ( , , ) ( , , )d d 0 a b mno m n e x y z x y z x y = 0 0 ( , , ) ( , , )d d 0 a b mne m n o x y z x y z x y =
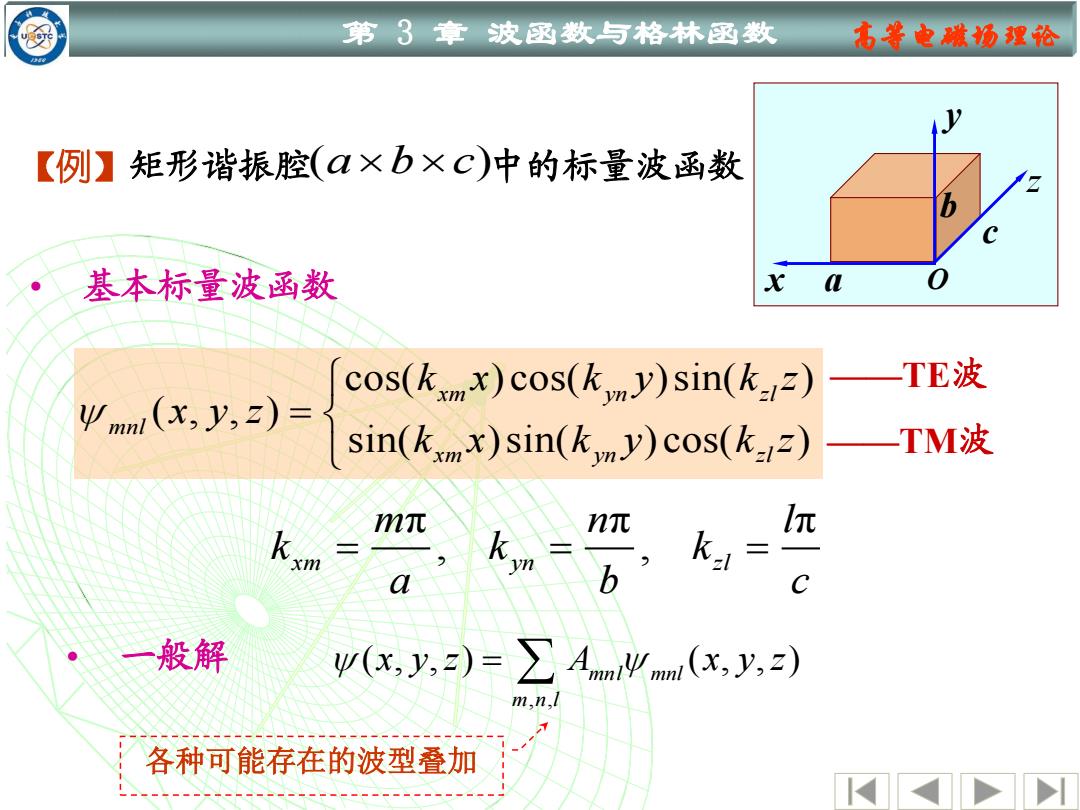
第3章波函数与格林函数 右等电微场理论 【例】矩形谐振腔(a×b×C)中的标量波函数 基本标量波函数 L cos(kmx)cos(ky)sin(k) —TE波 Ψmn1(x,y,z)= sin(km x)sin(ky)cos(kz)- TM波 m元 n元 l元 xm k1= a C 般解 y(x,y,z)=∑Any m(x,y,2) m,1n, 各种可能存在的波型叠加
第 3 章 波函数与格林函数 高等电磁场理论 • 一般解 , , ( , , ) ( , , ) mnl mnl m n l x y z A x y z = • 基本标量波函数 cos( ) cos( )sin( ) ( , , ) sin( )sin( ) cos( ) xm yn zl mnl xm yn zl k x k y k z x y z k x k y k z = 各种可能存在的波型叠加 ——TE波 π π π , , xm yn zl m n l k k k a b c = = = x y z O b a c 【例】矩形谐振腔 ( ) abc 中的标量波函数 ——TM波

第3章波函数与格林國数 右等电微场理论 3.1.2 圆柱面波函数w(P,中,z) 1 方程 1 8w p=0—奇点 基本解 w(P,中,z)=R(p)Φ()Z(z) 则 dΦ +v2Φ=0→Φ()=h(vφ) 在周期性条件下,V=n d'Z dz2 +k2Z=0→Z(z)=h(k.z) D2d'R dR do? +p +(k3p2-v2)R=0一贝塞尔方程 dp k2+K2=k2 (k。kz中有一个是独立的)
第 3 章 波函数与格林函数 高等电磁场理论 2 2 2 2 2 2 1 1 ( ) 0 k z + + + = 方程 基本解 ( , , ) ( ) ( ) ( ) z R Z z = 则 3.1.2 圆柱面波函数 ( , , )z 2 2 2 z k k k + = k ( 、k z 中有一个是独立的) ——贝塞尔方程 2 2 2 2 2 2 d d ( ) 0 d d R R k R + + − = 2 2 2 d 0 d + = 2 2 2 d 0 d z Z k Z z + = 在周期性条件下, = n ( ) ( ) = h ( ) ( ) Z z h k z = z = 0——奇点

第3章波函数与格林函数 右等电微场理论 ★圆柱函数 dR dR +(k3p2-V2)R=0的解为圆柱函数,即 R(p)=B(kp) 其中:B(u)~J(u),N(u),H(u),H2)(u) v+2m J(u)=∑ 1)" 2 V.(u)= J,(u)cosvπ-J_v(u) S1nVπ H"(w)=J,(u)+jW,(u) H2(u)=J,(u)-jN,()
第 3 章 波函数与格林函数 高等电磁场理论 其中: R B k ( ) ( ) = (1) (2) B u J u N u H u H u ( ) ( ), ( ), ( ), ( ) 的解为圆柱函数,即 2 2 2 2 2 2 d d ( ) 0 d d R R k R + + − = (2) ( ) ( ) ( ) H u J u jN u v v v = − 2 0 ( 1) ( ) ! ( 1) 2 m m m u J u m m + = − = + + ( ) cos ( ) ( ) sin J u J u N u − − = (1) ( ) ( ) ( ) H u J u jN u v v v = + ★ 圆柱函数