
网 第3章波函数与格林函数 右等电微场理论 标量波函数 矢量波函数 标量格林(Green)函数 并矢格林函数
第 3 章 波函数与格林函数 高等电磁场理论 矢量波函数 标量波函数 标量格林(Green)函数 并矢格林函数

第3章波函数与格林函数 名等电微场望论 §3.1标量基本波函数 讨论的问题: ·什么是标量波函数? 常用标量波函数与特点?
第 3 章 波函数与格林函数 高等电磁场理论 § 3.1 标量基本波函数 讨论的问题: ⚫ 什么是标量波函数? ⚫ 常用标量波函数与特点?
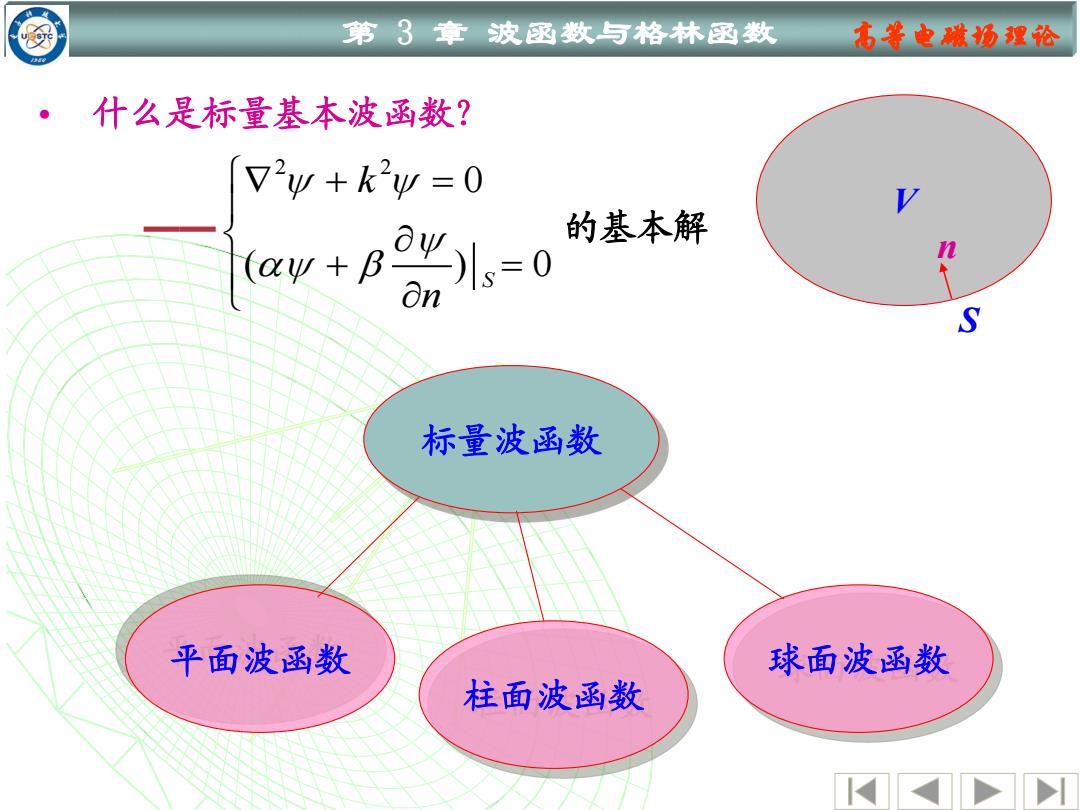
第3章波函数与格林函数 右等电微场理论 ·什么是标量基本波函数? 72y+k2yw=0 uw+Bi。-0 的基本解 S 标量波函数 平面波函数 球面波函数 柱面波函数
第 3 章 波函数与格林函数 高等电磁场理论 • 什么是标量基本波函数? 2 2 0 ( ) 0 S k n + = + = —— 的基本解 标量波函数 平面波函数 柱面波函数 球面波函数 V S n

第3章波函数与格林函数 右等电微场理论 3.1.1平面波函数Ψ(x,y,2) dX(x)+k2X(x)=0 方程 owovWrkw-0 dx2 Ox2 0y2 Y()kY(y)=0 dy2 V(x,y,=)=X(x)Y(y)Z(z) d2Z(2)+k2Z(a)=0 dz? 其中:k?+k3+k=k2(kx、k,、k中有两个是独立的) 基本解 w(x,y,z)=h(k,x)h(ky)h(k_z) cosu,sin u 驻波解 h(u)= ‘,em 行波解
第 3 章 波函数与格林函数 高等电磁场理论 222 2 2 2 2 k 0 x y z + + + = 方程 基本解 ( , , ) ( ) ( ) ( ) x y z x y z h k x h k y h k z = 其中: 2 2 2 2 x y z k k k k + + = cos ,sin ( ) e , e ju ju u u h u − = —— 行波解 —— 驻波解 3.1.1 平面波函数 ( , , ) x y z ( k x 、 k y 、 k z 中有两个是独立的) 2 2 2 d ( ) ( ) 0 d x X x k X x x + = 2 2 2 d ( ) ( ) 0 d y Y y k Y y y + = 2 2 2 d ( ) ( ) 0 d z Z z k Z z z + = ( , , ) ( ) ( ) ( ) x y z X x Y y Z z =

第3章波函数与格林國数 名等电微场望论 1、无界空间的基本波函数 kx、ky、kz取连续值,h(u)取行波解。 基本解 业(x,y,2)=A(kx,k)e1,+,*k:) =A(k,k )e 平面波 波矢量 其中:k=ekx+e,k+ek =k(e,sine cos +e,sine sin+e.cos) 中取不同的值,表示沿不同方向传播的平面波 般解(x,y,2)=J∬A(k,k,)edk,d, k W(x,y,z)的波谱或角谱
第 3 章 波函数与格林函数 高等电磁场理论 k k 、 取不同的值,表示沿不同方向传播的平面波 一般解 ( , , ) ( , )e d d jk r x y x y x y z A k k k k − = ( , , ) x y z 的波谱或角谱 1、无界空间的基本波函数 h u( ) x k 、 k y 、 k z 取连续值, 取行波解。 平面波 ( , )e jk r A k k x y − = 基本解 ( ) ( , , ) ( , )e x y z j k x k y k z x y x y z A k k − + + = 其中: x x y y z z k e k e k e k = + + ( sin cos sin sin cos ) x k k y k k z k = + + k e e e 波矢量 k x k y k z k k k