
将式(1.106)中之特确定函数g1()和g:()表示为如下级数形试:. -2An5,&e到-24ana (1.119) 式中A为待定系数,日:=议. (三)反对称荷载情形的解答 仿求解对称荷载解答的方法和步筑,求解边值问题(1.106)~(1.108)不难得到反对称 荷载情形的解答。略去中间推导过程,直接将有关的表达式和算式书列于下。 1.、立和而的装达式: a-2a[sinp.zsh5+sa邮inA g-宫+20Ra证+6a9z-en7+2ca9灯+w 可=j +2Roa5+Qahag-Ewa2+2cahahA+ 1.120) 支中R-岁GRy-说e,6-” 时+所 v(时一h Gsin(e)sintaGth.5 Qy一B, a+A. a;· 2.常数A、C及C。之确定 常数A:、C,及C。由如下线性代数方程确定: A品[告+月牛豆4x-a,-g2冻 C=a-A号-月aFa+宫4a6的 -a;EM]sina,, i▣1,2,3,… Ci=-2a空Rea+GaA-C.che jain一2 GeopehR.+合n (1.121) 式中名=2 + sh月e 含A-6A一re [a6N。-oBM- oa.Nim shB; Ha=i血(a二2+血e十2,La=28he腿,M=- 2Rsha03月 4-P1 + 的十隆 喉+阴 N4=一 2p,sh月cos8 i… 防十股 ,a6=2T,a=2Tcos9, 3.应力分量 将式(1.120)之在、m及每代入式(1.13)得如下应力分量表达式: 31 -………-…--
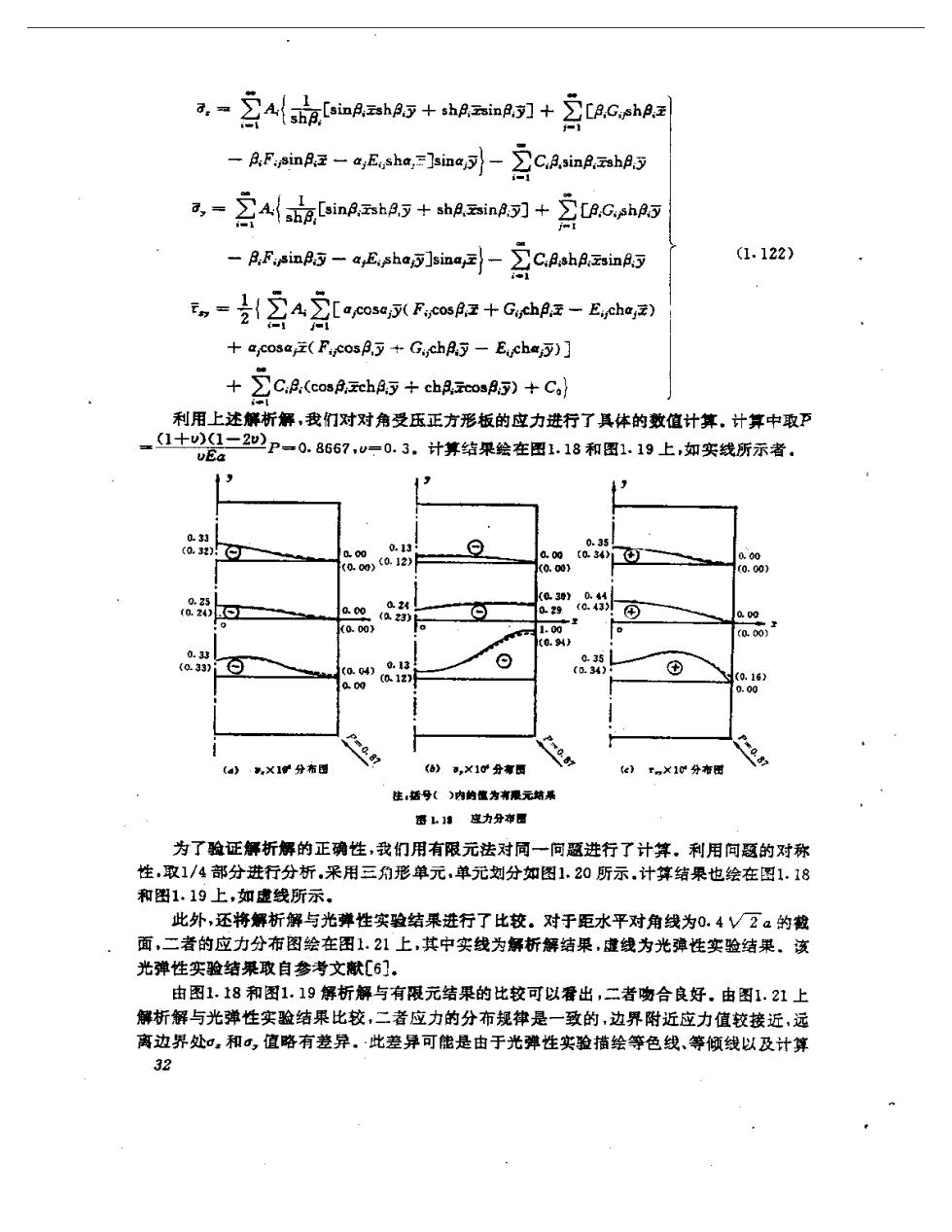
,-2A点oiaR,hp5+hinp.刃+习LAC.hPz 一p.F.ninPx-.Ehe,=Ane可-2 C/imp:zshp5: 司,-2 Lainh5+shpinD5.]+AA.Gph5 -AR,sin5-aEupho3]sina,-。夏C.Fohp,.zinA5 (1.122) =含2A2[6 oF.cP+G-Erbs2到 +a,cosa(Fcos月,+G,ch5-Echa)] C.B.(coch.3+chco+C 利用上述解析解,我们对对角受压正方形板的应力进行了具体的数值计算,计算中取℉ 一1十)-2w2p=0.8667,v=0.3,计算结果绘在图1.18和图1.19上如实线所示者. vEa 0.33 0.35 (0.32) 0.00 0.13 (a.00)0.12) a00【0.34)1) 0.00 (0.00 (0.0) 0.25 (030》044 04 (0.24)置⊙门 0.00(位.23) 029 (0.43 ⊙ a0 0.00) (0.94y @阳 0.33 o.33)i⊙】 ⊙ 0.35 (0.04) 0.13 (0.34) ⊕ (012) (0.16) 0.00 87 (a》·X1分布国 6》,×1心分有西 087 e)rn×10分布图 87 住:话号()内的值为有限元姑果 图上"应力分布四 为了验证解析解的正确性,我们用有限元法对同一问题进行了计算。利用问题的对称 性,取1/4部分进行分析,采用三角形单元,单元划分如图1.20所示.计算结果也绘在图1.18 和图1.19上,如虚线所示。 此外,还将解析解与光弹性实验结果进行了比较。对于距水平对角线为0.4VZα的截 面,二者的应力分布图绘在图1.21上,其中实线为解析解结果,成线为光弹性实验结果。该 光弹性实验结果取自参考文献[6]. 由图1.18和图1.19解析解与有限元结果的比较可以叠出,二者吻合良好.由图1.21上 解析解与光弹性实验结果比较,二者应力的分布规律是一致的,边界附近应力值较接近,远 离边界处加和σ,值略有差异。·此差异可能是由于光弹性实验描绘等色线、等倾线以及计算 32

1P-406M0 11 a1t⊙ (20】 (0.01) (a012》 a18 a17 Q016 a013) (0000)」 Q600 (a.的0 0.024 ① 0.22 a的 a00 (》,有(MN/) (a0) ()乌,母#温0N/) (d00) (e)t。分率■(M0/a) 注,塘号()内的蓝为有餐元墙限 西119应力骨菊福 单食,N/ (0.028) 0.019 (0.04) 0.012 0.012 QIV五 (0.013) 0 0.100 图1.20 注:括号()内的催为光弹结乘 1.21 方法(切力差法)等的近似性道成的。总之,以上比较证实了解析解的正确性。 §1一6平面边值何题的另一种解法 以上求解各种深梁应力分析的边值问题时,主要使用的是有限积分变换法,这里建议另 一种求解边值问题的方法,它也适用千前述各种深梁。为了清晰起见,下面以§1一3中所讨 论的简支深梁的应力分析为例,其体阁明该方法的原理及其运用。 如图1.6所示简支深梁,将荷装分解为如图1.?所示关于轴王对称和反对称的两种情 形,从而将简支深梁的应力分析归结为求解式(1.7)~1.52)的单个偏微分方程的边值问 题。这里用另一种方法来求解这些边值问题。 (一)对称荷载情形的解答 1.求解 将式(1.50)中之持确定函数f()及,()表示为式(1.j之级数形式。于是,由式 (1.50)有 器+骑-0 年(1.123) 王=士1,==】 ao5:y=士a.8-2aaaa 将边值问题(1.123)之解表示为 [P.chal+Q.chacoso (1.124) 33

其中P,及Q为任意常数.不难验证,式(1.124)已满足式(1.123)第一式之微分方程.其中常 数P:和Q由(1.123)中的边界条件确定,有 B: Q=chaid 将所得之P.及Q代入式(1.124),得 a- 2A恤+aag】 cha chai (1.125) 这里所得边值问题(1.123)之解(1.125)与31一3中所得解(1.57)是相同的, 2.求解和 将式(1.125)代入式(1.51),有 器+幕-[ -B,asina,tcha.y cha' chaA (1.126) 主=1, 夏-三As!5=士太需=-盖 将边值问题(1.126)之解表示为如下形式: Tcha,'Tcosa'y 2cha -42222+D (1.127) 式中C.及D,为任意常数,,=ix/。 不难验证,式(1.127)已满足边值问题(1.126》第一式之微分方程。其中任意常数C,和 ··D由边值问题(1.126)之边界条件确定。净式(1.127)代入式(1.126)之边界条件,有 D=】 A2若1+h)-1 A1若+yh)-1c,-Dcar0 i=1,2,3,… 2,l六sna-若ad+hw+caa -小广[24inaz近 (1.128) 式中G,=sin[a)l+simC上)A】,H,=2 tha/sina-2e,-n4 B + atal (a+a时 3.求解市 将式(1.125)代入式(1.52),有 臺+器-1吉[A3-a] cha' cha;A (1.129) 五士1, 要=-器了-士.票=-28oa王-) 将边值问题(1.129)之解表示为如下形式: 34

-22hR52+宫ra435+1±[4怎 2cha B.yehascona+Ey .2chad (1.130) 其中E,和F,为任意常数,=. 式(1.130)已满足边值何题(1.129)第一式之缴分方程,其中常数E,和F由式(1.129) 中之边界条件确定。由式(1,129)之边界条件有 A去h+0a+ 2a,l去h+oshal -∫引,ina 21结a+-]- 12,3 ER,ehBA- 五=2可1去a+灿a)-]粤- (1131) 式中 乙y=22 tha aina8_2时-c3)sinx 时十 (2)饺 =2牛典年2,系一t.R)opad2 +1 ag一月 4,确定常数A一F 式(1.125)、(1.127)及(1.130)中常数A、B、C、D,E及F:之确定除利用式(1.128)和 (1.131)之条件外,尚须利用下面两个条件: 玉=士1,=品器+ (1.132) 了=士,=2(爱+ 由式(1.128)、(1.131)及(1.132)之条件得到如下确定常数A,B、CsD,、E.和F、之线 生代数方程组: -宫4x地曾2-含g,如4- Aa,a 2Drca时 会,a月sA以-R=- sin a 宫4xa号2-a+宫a,g+caed aay +宫D.f..,o8pk,+2EAMe以- Di/lchp: 习4,l去(Q+2 Hsins以+a1先24+aa)+Cghe - 2ER,Rsh+2 F/Crim时h财-0