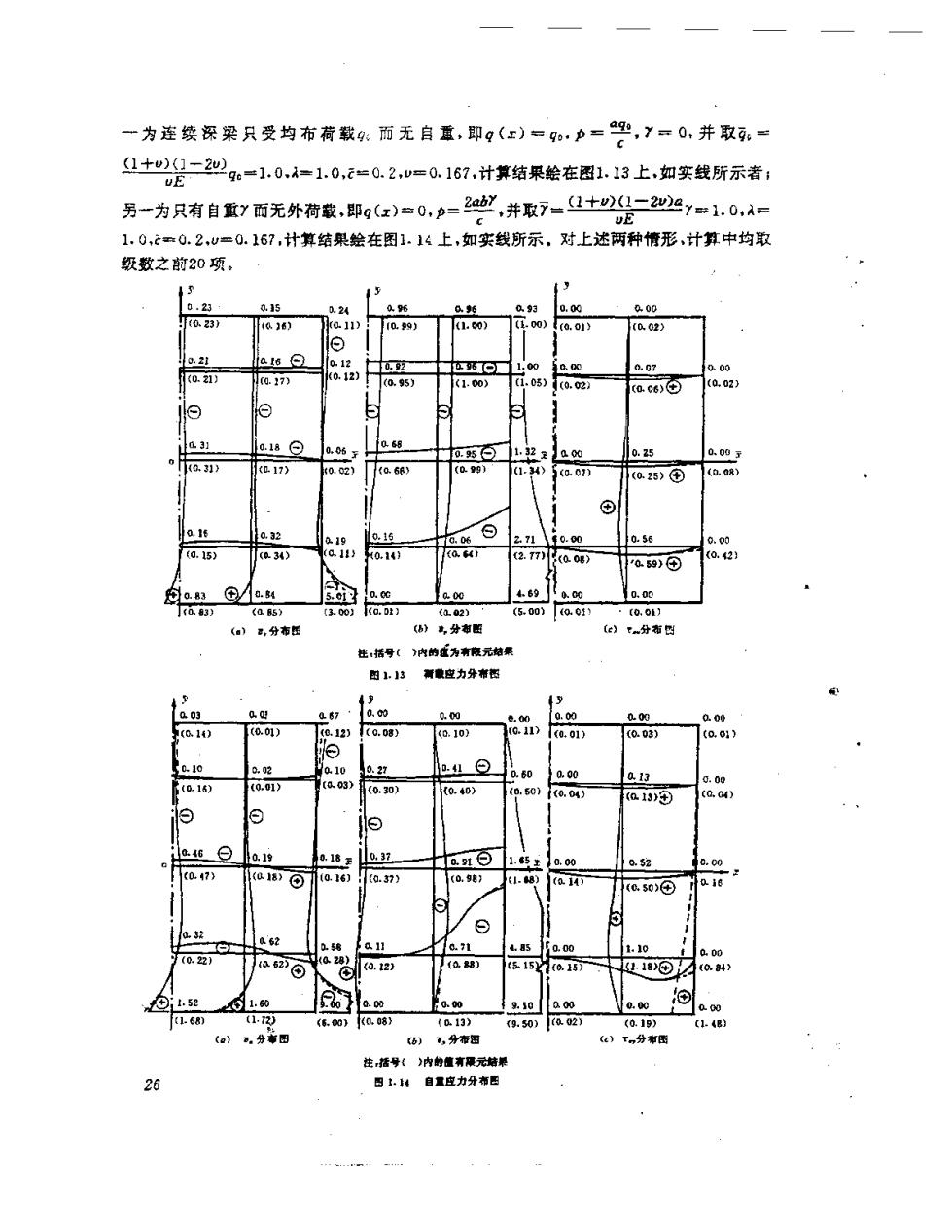
一为连续深梁只受均布荷载4:而无自重,即g(x)=。·p二,y=0,并取,= c 1+)一2业g6=1.0,=1.0,c=0.2,w=0.167,计算结果绘在图1.13上,如实线所示者: vE 另一为只有自重y而无外荷载,即g(x)=0,=2y,并取7=1+)一22y=1.0,A- 1.0,cm0.2,w=0.16?,计算结果绘在图1.14上,如实线所示。对上述两种情形,计算中均取 级数之前20项。 0.23 0.15 0.24 Q96 0.5 093 0.00 a00 (a.23) t016】 0.11) i099) (1.00) 1.00) 《a.1) (0.2 ⊙ 0.2i 1a16 0,12 0.2 6。■ 1.00 1.00 007 0.00 0.21】 (0.17) 0.12) (0.95) (1.00) 1.05) (0.02 a.06)⑤ (a,0z) 03】 0.18⊙ 0,6 0.9512 a00 0.25 0.003 KG.31》 (017) 0.02) 《a.6B) (0.99) (1.34) g.01) (0.25)① (0.08) ⊙ a.16 0.32 a19 0.16 0.06 ⊙ 2.71140.00 0.56 0.00 (0.15) (.34) (q1》 0.149 G4」 2.77)0og) (0.21 a59)④ 空a83 ①a.4 5.01 0.6 a.0c 469 0.0 0.00 J(083) (a85) 【3.00】 o.0t】 (002) (5.001 (0.01) ·(001) (■),分布图 我,分如图 (e》t分布因 注:括号()内的重为有限元站果 图1.13 新敬应力丹布西 3 a03 a 467 0.00 0.00 0.00 0.00 0.00 a.00 (01i) (0.01) (0.12) (0.08) (0.10) 0.11) (0,01) (0.03) (001) 0.10 0,02 a10 0.27 血19 0.0 10.00 (0.15) (0.01) 〔a.03) 013 0.00 (0.30) (0.40) (0.50)1(0.04 (013) (O.04) 0 白 a46旦 019 0.18至 0.32 0t曰 1.5上10.00 10.52 0.00 0.47) 018》⊙ (0.16) 10.37】 (0.98】 (1.8) 1(a.1 (C.50)④ 0.18 a.2 3 0.62 1.56 Q11 .71 4.85 0.00 1.10 a00 (0.221 (a62) (028) 0 (a.12) (0.B) 〔515y (a.15) 1.18)© (0.) f1.52 1.60 0.00 0.00 9,10 000 0.00 0.00 1-68) (1-72) 6,00) K0.a8》 (0.13) (9.50) (a.02) (0.19) (a) 。分事因 (b) ,分布图 注括号《》内的體有限元姑果 26 因1.4自量应力分布图

为了验证解析解的正确生,对上述两种荷载情形下连续深梁的应力,又用有限元法进行 了计算。计算中利用问题的对称性,取深梁右半部分为计算对象,单元划分如图1.15所示, 并利用51P5程序进行计算、计算结果也分别绘在图1.13和1.14上,如虚线所示。由图可以 看出,解析解与有限元结果吻合良好,远买了解析解的正确性。 §1一5对角受压正方形板的应力分析 如图1.16(a)所示边长2a的正方形板,在一对角顶点处受 大小相等方向相反沿对角线作用的压力P,不计板的封重,板 的受力为平面应力问题。 取如图所示之直角坐标系xo心y,将图1.16(a)之压力分解为 图1.16(⑦)所示两个相互正交的分力T=P/小/2.图1.16(b)中 作用在角点上相互正交的分力T,可视为作用在角点处相邻两 边界上之法向集中力,抑或视为作用在角点处相邻两边界上之 切向集中力。在以下的讨论中,我们将它们视为后者,即作用在 角点处相邻两边界上之切向集中力。 取正方形板边长之半长a为参考长度,在式(1.10)无因次 量的情况下,将图1.16()中之切向樂中力T表示为无因次量 图1.15 (0) 图1.15 r=PW2=4+)-2w)上,则图1,166文为器1.16c). V2vEa 为了简化计算,将图1.16(c)之荷载分解为图1.17(a)和(b)所示关于轴z和5对称和反 对称的两种情形。对于图1.17(a)的对称荷载情形,在云=士1及=士1边界上的分布表面 切间力可分别表示为()=0.57[6(灯一1)一(5+1)]及1()=0.5T[8(王一1)-8(宝十 1)],其中(t)为Dirac单位脉冲函数。对于图1.17(b)的反对称荷载情形,在五=士1及交=士 1边界上的分布表面切向力可分别表示为()=0.5T[8(+1)+6(灯一1)]及,(z)=0.7 [6(z+1)+8(z一1)]. 注意到不计板的自宜,则有X=Y=0,于是控制方程(1.12)成为 (1.99】 蹰 7=0,7m=-1甘票,了5-10等 v工苏 根据问题的性质,有如下边界条件: 27

T/2 T2 T/2 T/21 T/2 T/ T/2 T/2 /2 附1.17 对称荷载情形[图1.17(a)] 交士1,8.=0,2=干孟(y) (1.100) y=1,8,=0,x=干() 注意到式(1.13),条件(1.100)可写城 乏=士1, 爱- 夏=-需干24列 (1.101) 3=士1, 需=一,罗- 要千, 同理,对反对欧荷载情形[图1.17(6)]. =士1,器=-, 五 西 +24 江 正 =±1, 沈 (1.102) =一, 五 要+242 (一)对角受压正方形板应力分析的边值问题 综合控制方程(1.99)及边界条件(1.101)和(1.102),对角受压正方形板的应力分析归 结为如下单个偏徽分方程的边三司题: 对称荷载情形[图1.1?(a)] 1. 7范=0 (1.1C3) z=土1,=f1(⑤);)==1,e=f(2) 其中f1()及f()为待确定之函数。 2. 7标=一1十u速 v玩 (1.104) =士1, 器-:y1,离一爱于到 3. 7行a一1+ v苏 (1.105) =土1,霉=-需于24,5:=士,器=-到 反对称荷载情形[图1.17(b)] 1. 7拒=0 (1.106) x=士1,=士g():可=土1,=士g() 其中g1()及g,()为待确定之函数. 28

2. 7z=-1十u5 u吞 (1.107) 宝=士1, 爱-1可=士1,需=-+%国 3. 7节-1十速 ”的 (1.108) 玉=士1、是=-需+%⑤:y=士1,需=- (二)对称荷禁情形的解答 1.求解e 将式(1.103)中之特确定函数f,(⑤)和f2()表示为如下级数: g)-2Aeaa,国到-2Aeo (1.109) 其中A为待定系数,=(i一0.5)x, 于是,由式(1.103)有 骆+骑=0 (1.110) 芝=土1,e- 2AoaJ:y-士1,9=2 A.c 边值问题(1.110)的解为 A[cosa.Rcho+cha cos3] (1.111) 2.求解立 将式(1.111)代入式(1.104).有 夏+等-l片2A盖in-aama刃 z=士1, 爱=-立o:5=士1,需-一要干%a) (1.112) 利用有限积分变换法求解边值问题(1.112),有 红-2A2器Ef)-Fina-Gaa司+2 Cinh5 (1.113) g+aR-2的m2.G血色二2+地(e+92 式中F,=+"。求· 店十两 a,-B; 十月; 宁a条E-0.A-:8 G=+"、aG C为积分常数,由如下条件确定: C=a-j[,ine证+ai-123…4.11 其中 a;=-2Tsina; 3.求解 29

根据问题之特点,点(云,)处之a值与点(灯,)处之可值相同。故元之表达式可由π之表 达式(1.113)中将云和5相互置换来得到,即 -豆4空5g-g-caa+含csna,l5) 4.确定常数A:及C 式(1.111)、(1.113)和(1.115)中常数A及C.之确定除利用条件(1.114)外,尚须利用 如下条件: =士,品爱+离}或=士1,已器+》 (1.116) 由条件(1.114)及(1.116)得到确定常数A及C,的如下方程: hr[是+会ro+宫aX-a c“片+会m明 i=1,2,3… (1.117) -含A会器EM,-a61 式中X4= +宫器引o山器-tA-a6 ucha, 22,Ea一Rsna-Gaa+器器2E4, - -aGN)Ha=sin(asin(d.=-2Tsine. a;-3 a:十9 2sina, j0 L=2axchasina. a+好 M=2aBch3sing.j≠0,V4=2 a.chassina 应十 时十 5、应力分量 将式(1.111)、(1.113)及(1.115)之、a及可代入式(1.13)得如下应力分量表达式: 2A品oaia7+caaa别刃+会器Ee园 p.GchC.a.c0s.che3 馬-宫A点estg+刃+会5e四 F0se3-.h]C.achaco3m3 =z2A2[Asia明in了+Cph5-E,shA +月sinP(F:,sina;十Gsha注-Eshp)]· +Cadsinaisha:+sina3sha) (2.118) 反对称荷载情形的解答。 30