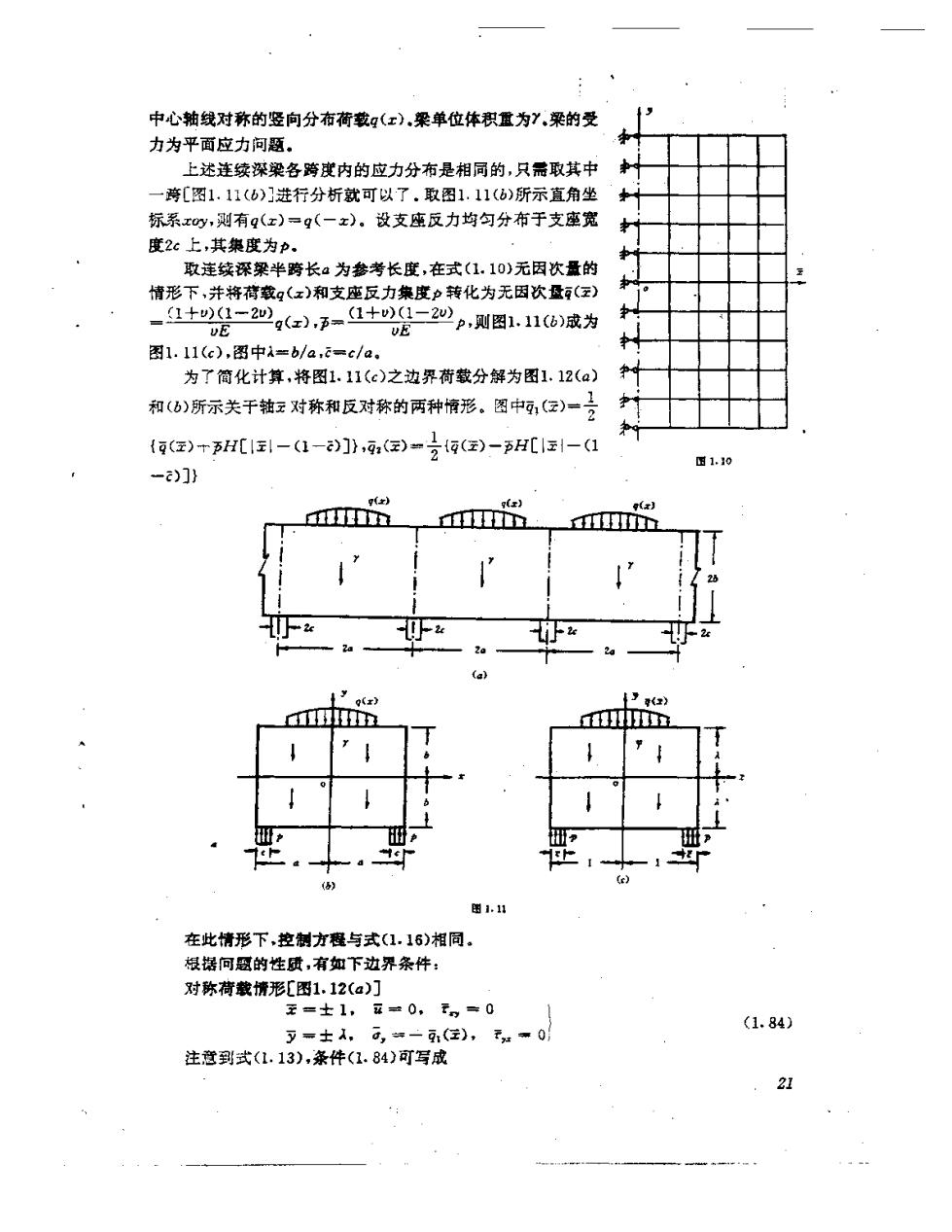
中心轴线对称的竖向分布荷我g(x),梁单位体积置为Y,梁的受 力为平面应力问题。 上述连续深梁各跨度内的应力分布是相同的,只需取其中 一 跨[图1.11(b)]进行分析就可以了,取图1.11()所示直角坐 标系xy,则有q(x)=q(一x)。设支座反力均匀分布于支座宽 度2c上,其集度为P。 取连续深粱半跨长a为参考长度,在式(1.10)无因次量的 情形下,并将荷载?(x)和支座反力集度p转化为无因次量(x) -+2没=2列a.=1+是=202,则图1.16减为 vE 图1.11(c),图中a=b/a,c=c/a。 为了简化计算,将图1.11(c)之边界荷载分解为图1.12(a) 和(0)所示关干转z对称和反对称的两种情形.图中,2~号 {(z)+3H[1!-(1-]》,:()-号{(z)-H1≥-(1 国1.10 -c)]} () (x】 x】 D D 2 (a} 1’x) y 人 t> e () 图1.11 在此情形下,控制方程与式(1.16)相同。 根据问题的性质,有如下边界条件: 对称荷载情形[图1.12(a)] 至=士1,a=0,7=0 (1.84) 习=士1,d=一(在),天aw0 注意到式(1.13),条件(1.84)可写成 21

P/2 /2 /2 /2 中n 讯中田 留 1 /2F邢/2 领量 (r) +7 (a) (b) 图1,12 王-士1,x=0, 西 =0 (1.85) 习=±, d而 =-一1(x), 市 时 莎 反对称荷载情形[图1.12(b)] x=士1, 云=0, =0 证 (1.86) 习=士太, 票-干,需- 器 (一)连续深梁应力分析的边值问题 踪合控制方程(1.16)及边界条件(1.85)和(1.86),连续深梁的应力分析归结为如下道 个偏微分方程的边值问题: 对称荷载膏形[图1.12(a)们 1. 7e=0 x=+1,=f1();-士A, =f() (1.37) 其中f1()及∫()为待确定之函数。 2. 7m--1+u y五 (1.88) 王=之1、=0;=工, 冠 3. 可罗=-1+v函 )苏 *(1.39) x=1, 器=0,9=士,离--a 莎 反对称荷载情形[图1.12(b)门 1. 722-=0 元=士1,e=g1();y=士入,e=g(x) (1.90) 其中g1()和g(x)为待确定之函数, 2. 7a=1+u速 v安 (1.31) E=:士1,4=0;下=士, 22

3. 可场=-+27 (1.92) 无=士1, =0:y=士,需-年() 正 衍 仿§1一2和§1一3中所述的方法求解边值问题(1.87)~(1.92),不难得到对称荷载情 形和反对称荷载情形的解答,这里不拟赞述,直接给出有关的表达式和计算式。 (二)对称荷载情形的解答 1.e、u和的表达式 chazcosB.cosascha cha chaa a=字A2maw9+22阳hy+2ca加Aad0 -君宫o2a3-套a2%aa-y G -Hsha5-】 ∑a:cos日g N(9;)g,(A) (1.93) 式中 B,=L十 a E 28,sha.'cosA (a2+3,)cha;, E,'=- a+好 F,=1止” a.F F,= sin (a;) sin(a÷3:) "(a2-3,2)cha.x' 4-3 年÷3, G,=1+ a,'G' u(a.)cha., G.= 2a.'sha,'cosA 2十3:7 H,=£工y a:H ”a2-caaA',H,= sia(a8 sin(a8) 4-3 十: :, j=0, g(A)= .1 j立0 2,j=0 》=1shy,j≠0, 3h,,j于0' N)=1,j≠0 4=J1(z)cos8,2近,4=i-0.5)x,a'=(-0.5)x/a,3,-jr 2.常数A,、B及C之确定 节数A,、B:及C、由如下线性代数方程组确定: AXu 含a-含aa=-z B}- 2in- 立C,2Neh3,=-6 i1,2,3,… (1.34) 宫4+28x-Ca2-a2 】 ,式中 Y..=I-i + 含器ac一A2小、又- w0 aLacosp. Yw= aacha-F 23

-宫p.P,Nube.. X=(a,'E-BG)sinaj th(e,H,che)had.d 2sing,' j=0,M,=2'chaksina以 a+a1 Lo= 2aech甲,sina以 a十 j≠0,V,-sia2+sin(a+2 a,-f, a:+月, 3. 应力分其 =豆A[色a器5+2Ewow司 cha, +2可3+宫a2xaa+2caaa25 cha, 3-含4器7-名器aiaj+宫a融 cha. cha;A +习影aea-)-Hahj- 怒 N(9,)g(A) =号宫4宫服-a8na了 h32(aH,ha,A-Hf)-3,Hsha小sin3z chaA 立Ca.sind.zabP.-】 u.sind,zsh. chA (1.95) (三)之对称荷载情形的解答 1,e、和元的表达式: chA'Tsin/cosa.shay cha, shaih 09<g.'rso3z808"、H1 Caind.ah2 亨小宫25-宫9空ao82为 会新+会5+分+合n, dsha (1.96) 1a平-90e,,= 式中E,=1+"E F,' 32中2 ”.(a2-月,2shad F财-a二2_inat2,G,=1t" 4一F: a4+, ”(8+chA, G-2BishB:'cosB 9+2 a二ha:H,-na2+na+2 H=l+”cH a;-Bi a十9; 24

Q0,4-ico3z证 2, a=(-0.5π,=深1A,=m、V》= j=0 j≠0 2.常数A:、B:及C之确定 常效A,、B:及C、由如下线性代数方程组确定: AXw-】 8Y,-2cLa8=2 ▣1 a÷-2a,-盒C.a.N,bPA-=-A =1,2,3,… 1.97) 身4x-含ay-c3aha-品 武中六=1, o0G-,i名y=g,G.-月/8,c Yw=】 5器0a-)-..,=2aNa Z= 宫-R、,=-二2+ hA c-3: 4+3 +1 Yi (aFs -3.Hx)cha-3.Q.chA.A.o.=q()cosa,id =1 乙g=- 2Ash8,Acos ,说,=一 28:'sha.Acosp ,2十2 &.2+3 D,为代装深梁沿轴了方的刚法互移,斋利用深染的位移约束条件来确定。列如,发竺 示原点处冠*0,则有 0,=-2a2+三0豆Q,-豆+三品 应力分量: 3,-亨A235-三0nry +2a3-至球a员xha+8caa0abA5 含4需2-会器oam+宫器 chd. 一2an5-路1cz- 了a0e8hg5÷列 she,A 号宫+月8-6,mc3+官含a+,dao -3,Qch9,jsin÷ 户caa2a订← asing,cchiy (1.98) 利用上述解析解,我们对连续深梁的应力进行了具体的数值计算。计算分为两种情形: 25