
D.'cha!Zu 宫AXs-BX+Caia-6 宫AX,-宫aX+6ca+ (1.73) 24-2ar。- Cr,Resine,-D.aisha!= -1,2,3,… 式中 Xw=+】 N(B) Yw- Zw=- 三 aTCOsB X别=】 cosB.' WP)gδ' N( (LaVa-a时EnU) y=+ a.FucosB. N(3.) .X=】 .Nia. Zv=- e Yo= N(MshBd-H.sho). Xw= a(Lusbp:-Easha) Yu= 宫3 F.Qasing, =sn&二-sine,±2) -3 g.+3 Py= 2ache,sina, 24= sint(a)]sin[(a] a,2-a a,-3, a'+9。 Sy= "a,'cha,isina' 2a,cha.'sina. a,-a2 6,÷ag Ry= 2a.cha;isina,' u-a2 2singA k=0, 2sina k=0 T4= 2aAchBrasina,'A V= a,2+32 也≠0, 2aA'chA'sing ,2中 产0 6=a国)com经 5.应力分量 由式1.?3)之代数方程组确定常数A、B、C和D后,将它们代入式(1.57)、(1.67)和 (1.9)之、云韵式子中,然后再将、立剂罚的表达式代入式(1.13)中即得到应力分量的 表达式: J: cha, 会器,国-E到 "cosazcha,3 chaA 宫ao万j+含C.xozchaJ 多出器22-会pa+2a cha, chaA 宫器+2a士ww柔了 N(P,)g;() 16

,=空A[C,im,a了-学,s-Eaba国到i5] 2a2[.inw.ToinB!行-月(MhA7-ghain]月 Coaia.sheh's + 习0g chA (1.74) (三)反对称荷载情形的解容 1.求解 将式(1.53)中之特确定函数g1(了)和g2()表示为如下级数形式: a⑤)-2 inp!,a国)-2 .co. 式中A:和B.为待定系数;a=(i一0.5)x,,=x/A 于是,边值问题(1.53)之解为 [A出+aa i- cha! sha (1.75) 2.求解π 将式(1.75)代入式(1.54)中,仿对称荷载情形下求解π的方法,利用有限积分变换法求 解边值问题(1.54),得 a=宫22ug-g-君a2吉ra5 +Cshe.Ssino. (1.76) ,a二c,E-血a】ihte+g以 产1 式中E=十 E a-, @;'+, F=1+0 aFif ”(a2-aj2)sha d' f=2 cho,isina以 B:EchB!-E:! a2十a,2 Ly= a;cha a;'=(j一0.5)x/a;C:为积分常数,由下式确定: C.a,cha=- sino:id,t=1,2,3,… -l,+ (1.77) 3.求解司 将式(1.75)代入式(1.55)中,有 票+器=-1片2[48585+Bo+列 i=1 che' sha 1.8) x=士1, 荒-需:3=士,需-车8cosz干元) 在此情形下,如果用有限积分变换法求解边值问题(1.78)将会遇到一些麻该,因此,我 们采用另一方法求解边值问题(178). 将边值问题(1.78)之解表示为 -[D.chA/zosp/3+E.cosP.zchp.y-L告”2[A TshTcos 2ch +a]+ (1.79) 17

式上和E,为任意常数,3:=x, 不验证,式(1.79)已足(1.78》第一式之微分方程,其中常数种E,将由式 (1.78中之两个边界条件予以确定。将式(1.79)代入式(1.78)的边界条件2,有 2A1若c9+hG,-d-Eshp)] +宫a[学-1去若总n-2 Cnin 会DAG,sip=4 a =1,2,3,… (1.80) 81-1若(1+月+2,N点=-a,1=1,23 (1.81) 式中 0;2 o年02,G,=ng2+5ince+22☒ H.=2a sha,isinal1 aacha:ksina! (a一月,) (a,+3,) M.=2cha inal ”+1 2,,=ng2+aa,a=z)cse,z在 8--3 a十B; 式(1.0)和(1.81)中不包含常数D,和E,故它们的值未定。由式(1.79)可以春出,(D。 十E)代表梁沿轴下方向的刚一位移,须利染的位移:束条件来确定。例如,设在坐标原点 处=0,则有(D+E)=一】 (D,+E)。 4.确定常数A、B,C,D及E 同样,式(1.75)、(1.76)及(1.79)中常数A:、.C、D和E:的确定,除利用式(1.??)、 (1.80)和(1.81)之条件外,尚须利用式(1.71)和(1.72)的两个条件。最后,由上空三个条件 得到确定常数A:、B,C、D,和E:的如下线性代数方程组: A(-12若Aag)+DBeh-2E,5cos明,=0 1-1去(1+2+会,Rsh=-a A-B.Y+C.orshe,d= 盒ax-al岁-cw- 2u 2arRo E.ARvchAi 会4K+axw-豆Cp..in-2 D.R/G.wbp财- 4Ysina, ah i=1,2,3,… (1.32) 式中 ×=习agoZ财5w.X-1克±o82 A 2 ch y:G (hsha!) 18

号+会i咖-(学-岩治)4 20 sha Al S=- 2半.-2a,- a.chB,'sina, + Pi= 器,Q 28:she:'sina 2(-a)cha'sina + (a2+9,2) R,= sin(a-A)sin(a:+B;) d-月 (+) 5、应力分盘 将式(1.75)、(1.76)和(1.79)之、立和元代入式(1,13)即得到反对称荷载情形下的应力 裘达式: a=】 chn3迈+】 -1 che (-it.rho/z-iny oo尘了6 shad -房2+去岁 che, che," +2a时9-1岁恤7+e到 sha,A -2 DA:P时ar灯+2 jcsi明ah5 -引宫A-告生+到5 ch: +含头(ha三-3)+2可1去经a2 shaA 会in.cae-2 in.5 宫D/h/5- E.sind.tch+ (i,83) 利用上述解析解,我们对简支深梁的应力进行了具体的数值计算。计算分为两种情形: 一为简支深柔只受均右荷载g:而元自重,即q(x)=9a户=兽,7=,并取: +)一2业g6=1.0,A=1.0,=0.2=0.167,计算结果绘在☒1.8上,知实线所示者: UE 另一为只有自霞y而无外荷载,即u(z)=0.2=2,并取7=÷)9一207=1.0,= E 1.0,c=0.2,u=0.167计算结果绘在图1.9上如实线所示。对上述两种情形,计算中均取级 数之前20项。 为了验证解析解的正确性,对上述两种荷载情形下简支深梁的应力,又采用有限元法进 行了计算,计算中利用问题的对称性,取深梁右半部分为计算对象,单元划分如图1.10所 19
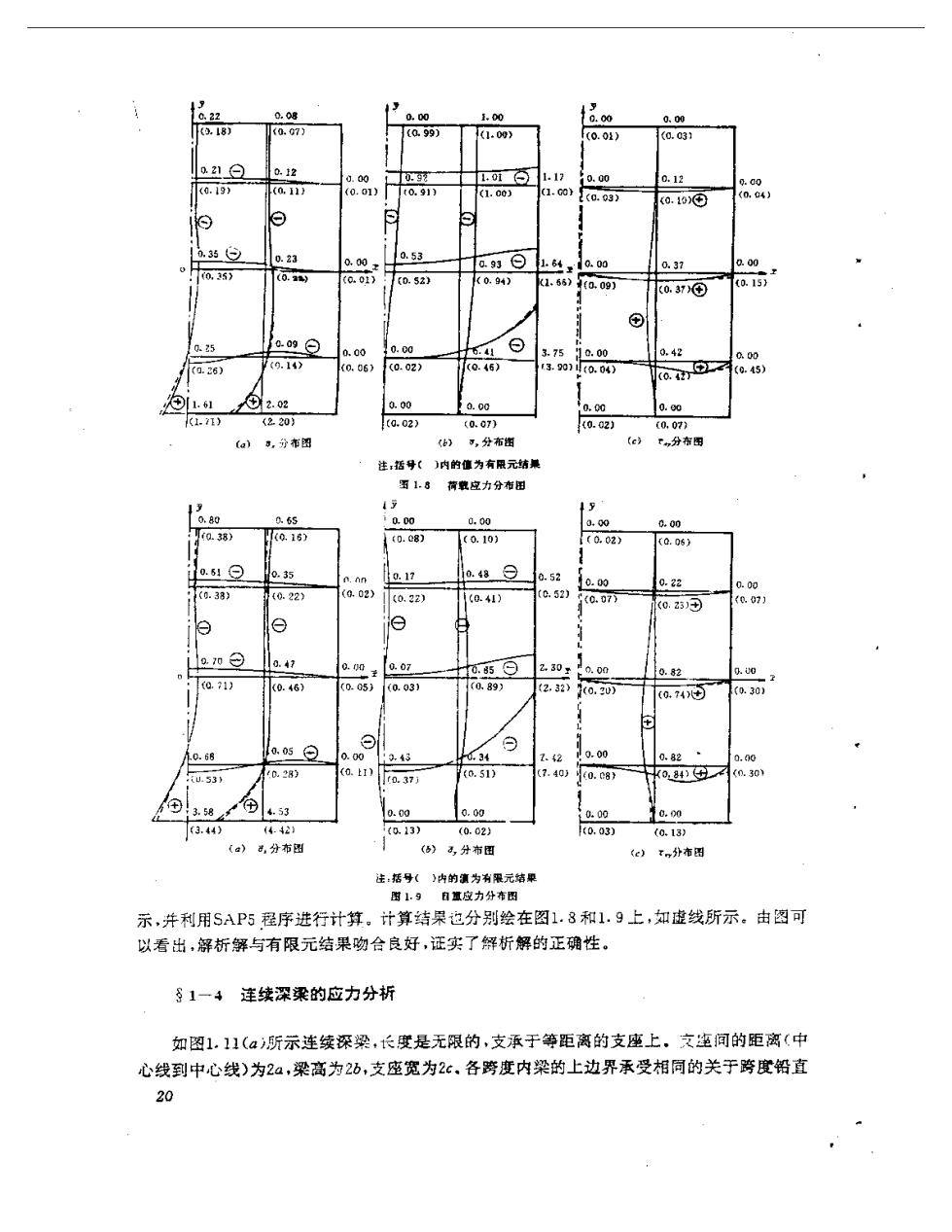
0,22 0.00 1.00 0.00 0.00 .18) (0.07) (0.99) 1(1.09) (0.01) (0.031 10.21白 0.12 0.00 1.17 0.00 0.12 0.00 (0.19) (0,11) (0.01) 1t0.91) (1.00) (1.00) 1(0.03) (0.15)⊙ (0,04》 ⊙ 035⊙ 0.23 0.00z 0.53 a939 .64xa.0o 0.37 a.00 0,35) (0.y (01) (0.5z) 0.94) 1.55)0.09) (0.37④ (0.15) ① 025 a09⊙ 0.00 0.c0 6.41 a 3.7510.00 0.42 000 (0.26) (9.14) 0.06 (0.02) (Q.46) 13.901i(0.04) a② (0.45) 1.1 2.02 0.00 0.00 0.0 0.o0 1.7E) (220) (0.02) (0.07) (0.02) (0.07) (a ·,分布图 (),分布扭 (e) F,分布田 注:括号〔)内的值为有限元结桌 图1.8 简璧应力分布田 17 0.80 0.65 10.00 0.00 a.00 0.00 0.38) (0.16) (0.c8) (0.10) 1(002) (0.05) 0.35 e.on 0.17 0.48⊙ 0.52 0.00 0.22 0.00 (0.38) (0.22) (0.02) (0,22) 1(0.41) (c.52】 (0.07 0.23④ (0.07) p 0.70⊙ 0.47 Q.00 0.07 o5⊙ 2.30 0.82 0.00 0.1) (0.46) (0.05) (0.03) 089) (2.32)(0.20) (0.74)d (0.30 p .0.68 0.05 ⊙ 0.00 .43 34 1.2 10.00 0.82 0.00 u.53y 0.283 (0.上I) (0.51) (7.40 t0.37j 0.08》 (0284)G (.30 3.58 ⊕ 4.53 0.00 0.00 0.00 0.00 (3.44) 4.2) t0.13) (0.02) 0.03) (0.13) (a》8,分布图 (5),分布图 (c)x,分市图 注:括号()内的演为有限元结果 图1.9自重应力分布图 示,并利用SAP5程序进行计算。计算结果也分别绘在图1.8和1.9上,如虚线所示。由图可 以看出,解析解与有限元结果吻合良好,证实了解析解的正确性。 §1一4莲续深梁的应力分析 如图1.11(α)所示连续深梁,长度是无限的,支承于等距离的支座上.文速间的距离(中 心线到中心线)为2a,梁高为2b,支座宽为2c,各跨度内梁的上边界承受相同的关于跨度铅直 20