
表1.1=0.5截面上应力分量a之值 级数项数 x=10 n些15 n=20 n=25 n=30 1.0 -0.55691 -0.43519 -0.52621 -0.60792 -0.59432 0.8 -0.18332 -0.17868 -0.17956 -0.17750 -0.17861 0.6 一0.07360 +0.07331 -0.07308 一0.07290 -0.07277 0.4 -0.05107 -0.05054 -0.05104 -0.05056 一0.05093 0.2 -0.04215 -0.04216 -0.04215 -0.04212 -0.04209 0.0 -0.03339 -0.03317 -0.03337 0.03318 -0.03333 0.2 一0.02450 -0.02449 一0.02448 一0.02447 -0.02446 一0.4 -0.01646 -0.01648 -0.01547 -0.01647 0.01648 -0.6 -0.00775 -0.00790 -0.00798 一0.00803 -0.00806 -0.8 0.01718 0.01579 0.01596 0.01547 0.01571 -1.0 0.09963 0.07445 0.11059 0.12592 0.11492 表1.2x=0.5栽面上应力分量8,之值 纸数项数n 元坪10 t=15 n=20 H✉25 n30 1.0 -0.99013 -1.00573 -1.00203 -1,00130 -1.0006 0.8 -0.91882 -0.91960 -0.91754 -0.91897 -0.91711 0.6 -0.74356 -0.74197 -0.74116 -0.74073 -0.74048 0.4 -0.57584 -0.57514 -0.57412 -0.57430 -0.57360 0.2 -0.44180 -0.44111 -0.44072 一0.44050 -0.44038 0.0 -0.33408 -0.33387 -0.33349 -0.33357 -0.33329 -0.2 一0.24408 -0.24399 一0.24390 -0.24384 -0.24382 -04 -0.16562 0.16578 -0.16584 -0.16586 -0.16588 -0.6 一0.09404 -0.09445 -0.09462 -0.09469 -0.09472 -0.8 一0.03106 -0.03090 -0.03142 -0.03109 -0.03149 -1.0 -0.00000 -0.00000 -0.00000 -0.00000 -0.00000 表1.3 =0.5裁面上应力分量T,之值 级数项数n 罗 n210 #=15 n=20 n平25 m=30 1.0 0.00000 0.00000 0.00000 0.00000 0.00000 0.8 0.22559 0.22724 0.22769 0.22813 0.22815 C.6 0.35409 0.35448 0.35472 0.35486 0.35494 0.4 0.37410 0.37390 0.57371 0.37379 0.37367 0.2 034723 0.34670 0.34648 0.34637 0.34633 .0 0.30968 0.30921 0.30885 0.30884 0.30868 -0.2 0.27473 0.27420 0.27396 0.27383 0.27379 -0.4 0.24316 0.24286 0.24257 0.24259 0.24245 -0.6 0.20473 0.20461 0.20454 0.20450 0.20450 -0.8 0.13379 0.13418 0.13415 0.13429 0.13419 -1.0 0.00000 0.00000 0.00000 0.00000 0.00000 从表1.1~1,3可以看出,取级数前10项至15项时,除个别值外,小数点后两位数基本 相同;取级数前20项至30项时,小数点后三位数基本相同,即取级数的项数大于20时,小数 1
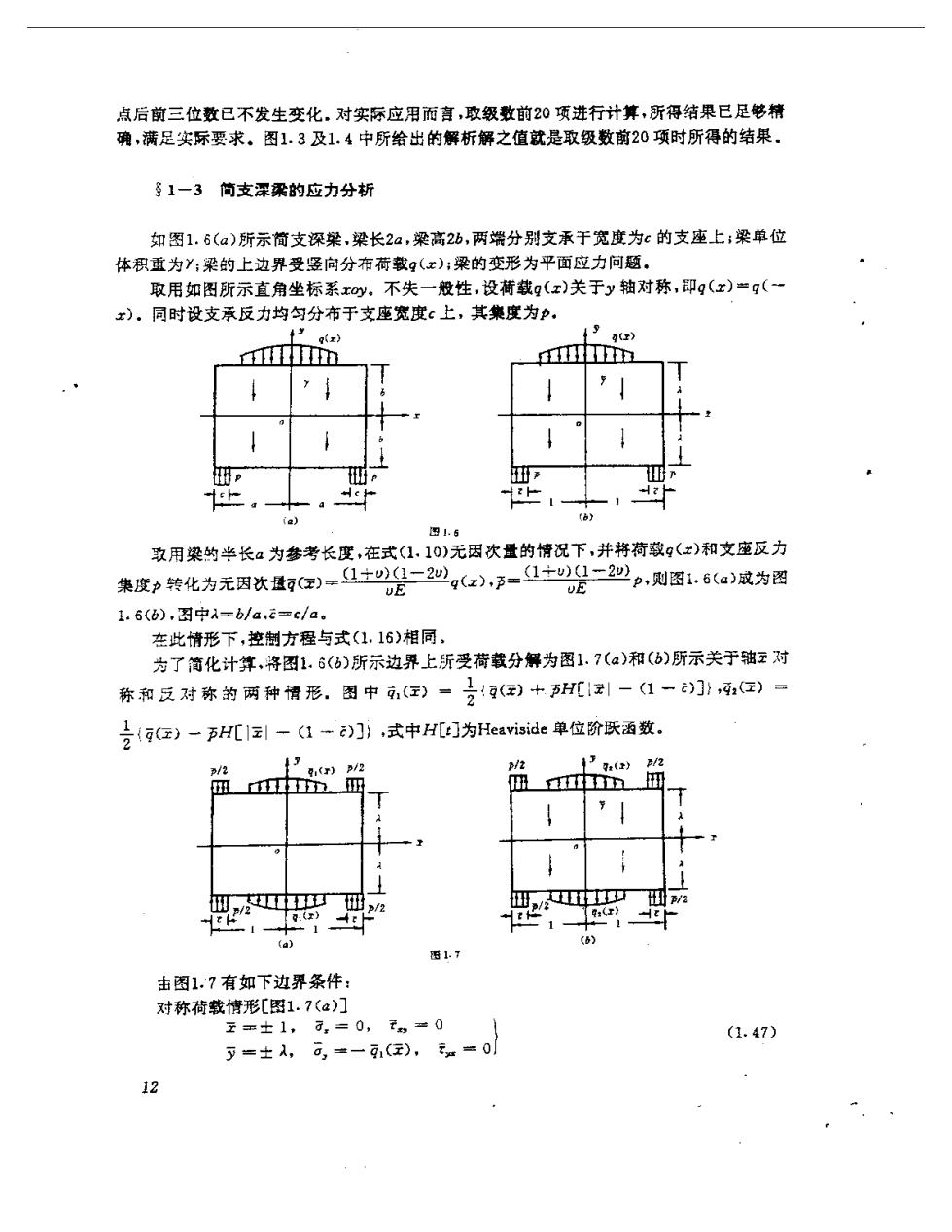
点后前三位数已不发生交化,对实际应用而喜,取级数前20项进行计算,所得结果已足笔精 确,满足实际要求。图1.3及1,4中所给出的解析解之值就是取级数前20项时所得的结果. §1一3简支深粱的应力分析 如图1.6(a)所示简支深梁,梁长2a,梁高2b,两端分别支承于宽度为c的支座上;梁单位 体积重为Y;梁的上边界受竖向分布荷载9(x):梁的变形为平面应力问题, 取用如图所示直角坐标系xy。不失一般性,设荷载q(x)关于y轴对称,即g(x)=g(一 x)。同时设支承反力均匀分布于支座宽度c土,其集度为p, g(x) h五 c ia) b) 图1.6 歌用梁的半长a为参考长度,在式(1.10)无因次量的情况下,并将荷载g(x)和支座反力 集度p转化为无因次量)=1+是-2必心g(z,3=1中0二2 2p,则图1.6(a)成为图 UE E 1.6(6),图中λ=b/a,c=cla。 在此情形下,控制方程与式(1.16)相同。 为了简化计算,将图1.6()所示边界上所受荷载分解为图1.7(a)和(6)所示关于轴云对 陈和反对弥的两种情形.图中)一合)+到-1一门}2)一 是c)一五H[1z引-(1-]》,式中H[的为Hevi单位阶跃函数. p/2 13() /2 p/2 ,中田2 /2 ta) (6) 西1.7 由图1.7有如下边界条件: 对称荷载情形[图1.7(a)] 王=士1,,=0,t=0 (1.47) 万=士λ,可,±一可1(F),。=0 12

注意到式(1.13),条件(1.47)可写成 王=土1, 新 =一e, 而 缸 近 一 而 (1.48) 万=土, 元 莎 =ē9(z)、 污 反对称荷载情形[图1.7(b)] z=土,器=-6, 妥 的 :.49) 可=士, 而 西 匠 (一)简支深梁应力分析的边值问题 综合控制方程(1.16)及边界条件(1.46)和(1.9),商支深梁应力分析的问题归结为如 下单个编微分方程的边值问题: 对称荷载情形[图1.7(a)], 1. 72e=0 (1.50) 元=土1,e=f(5);=±A,e=f() 其中f1()及f,()为待确定之函数, 2. 7五=-1土”花 y妥 (1.51) 元=土1, 委 3. 7行=一1十”茂 y (1.52 无=士1, 器=-影了=士需=--到 z 反对称荷载情形[图1.7()] 1. 72=0 (1.53) 工=士1,e=g:(灯);y=士A,e=士:()f 其中g1(y)及g2(x)为待确定之函数. 2. 72z*-1土“速 U近 (1.34) 玉-士1,爱=-即9士爵=- 蔻 心 可河-1十”票+27 0万 (1.55) 主=士1, -需了士 =-e干2(z) (二)对称荷载情形下的解答 1.求解 将式(1.50)中之待确定函数f:()和f()表示为如下级数形式: f)-2Aa5.4②-2a2 (1.56) 式中A:和B,为待定系数,a=(t一0.5)x,a±(i-0.5)x/1。则边值问题(1.50)之解为 13

互+aoga] cha: chad (1.57) 2. 求解 将式(1.57)代入式(1.51)中,有 碧+赛-告[a器-4器到 chaA cha (1.58) 王=土1, 是-宫o5:3=士,需=-要 用有限积分变换法求解边值问题(1.58).式(1.58)之边界条件均为非齐次的,为了避免 Gibbs现象,设 立点品1十经 (1.59》 其中立和立:分别为如下两个边值问题的解: (1) 0+9-1片[a05-A地] chaA cha (1.60) 元=士1, 可=, 焉=0 (2) +-0 (1.61) 产÷士1, 爱-0,5-士旁一爱 求解达值问题(1.60)。 将式(1.60)关于)进行积分变换,并取用如下的积分变换式: 广+A 正变换: 宝.)=匠)s时54的 (1.62) 逆变换: (花,)= 含器 式中 3)=π1入, (2)=/2,j=0 1λ,≠0 利用式(1.62)之积分变换式,可求得边值间(1.60)之解 豆含爱鄙Lu出-w-84空m (1.63) 式中 E,=1土u aEid ”a2-cha, Esin(]sin[ g,-37 a十3 P=土g aFif ()chai F.ashadcos Echa +月" ·(1) j=0, 1. j=0 f)={shR时z,≠0. f(1)= ch,,≠0 求解边值问题(161)。取用如下积分变换式: +1 正变换: (4)=a,(,)si恤2 o3a2 (1.64) 逆变换: ,(运,》=】 14

式中a;=(j一0.5)r,则可求得边值问题(1.61)之解 Csina,zche (1.65) 式中G,为积分常数,由如下条件确定: Caba-[i在,i=L2,3 (1.66) 将式(1.63)及(1.65)代入式(1.59)中,得 五= 含4会爱器国-到 亨a2mao5+2 Cain.时 F (1.67) 3.求解元 将式(1.57)代入式(1.52),有 是+幕-1告2[4-a] cha chaA (1.68) 云=±1, 是-票y-士,需=-28e-a因) 仿求解边值问题(1.58)的方法,不难求得边值问题(1.68)的解 一 宫0aana7+含宫Mug5)-ha D.hsingy +】 cos8zg(⑤) V(p)g:() (1.69) 式中 号a平a,G-a8,H,-+"影 G=1” aGi a+ (a-)cha;d H=2+迎2..=.o,-z)coBzdz a,-9; a+3: g(A) 3,=0, g)=sh3,i≠0, 8()=: 1,=0 ch3,、j≠0 2,j=0 a=-0.5)/,3=,V(g,)=11,≠0 D:为积分常数,由如下条件确定: D.o!shalsinai =1,2,3,… (1.0) 4.确定片数A:、3、C:及D 式(1.57)、(1.67)及(1.69)中之常数A,3、C及D,尚是未知的,它们的确定除利用条 件(1.66)和(1.70)外,尚须利用如下条件: 玄=士1,=心器+》 (1.71) 可=士2爱+》 (1.72) 利用条件(1.71)、(1.72)、(1.66)和(1.70)得到确定常数A、B、C,和D:的如下线性代 数方程组: 15