《机电一体化系统设计》课程教学资源（讲稿）机电一体化讲稿（共六章）

年月日 量。 2粘性阻尼系数的折算 机械系统的相对运动元件之间存在着粘性阻尼，并以一定的形式表现出来。在机 械系统的数学建模过程中，粘性阻尼同样需要折算到某一部件上，求出系统的当量阻 尼系数。其基本方法是将摩擦阻力、流体阻力及负载阻力折算成与速度有关的粘性阻 尼力，再利用摩擦阻力与粘性阻尼力所消耗的功相等这一原则，求出粘性阻尼系数， 最后进行相应的当量阻尼系数折算。 在本例中工作台得摩擦损失占主导地位，其它各环节的摩擦损失相对而言可以忽 略不计。 当只考虑阻尼力时，根据工作台和丝杠之间动力关系有 T2π=cL (2-16) 即丝杠旋转一周所做的功，等于工作台前进一个导程时其阻尼力所做的功。 根据力学原理和传动关系有 -a会 将以上两式代入式(2-16)，并整理得 - (2-17) 式中c'一一工作台导轨折算到轴I上的粘性阻尼系数 -aj (2-18) 3刚度系数的折算 机械系统中各元件在工作时受到力和/或力矩的作用，将产生伸长（或压缩）和/ 或扭转等弹性变形，这些变形将影响整个系统的精度和动态性能。在机械系统的数学 建模中，需要将其折算成相应的当量扭转刚度系数和/或线性刚度系数。 在本例中，首先将各轴的扭转角折算到轴I上，丝杠与工作台之间的轴向弹性变 形会使轴II1产生一个附加扭转角，所以也要折算到轴I上，然后求出折算到轴I 上的系统的当量刚度系数。 1)轴向刚度系数的折算当系统受到载荷作用时，丝杠螺母副和螺母座都会产 11

年 月 日 11 量。 2 粘性阻尼系数的折算 机械系统的相对运动元件之间存在着粘性阻尼，并以一定的形式表现出来。在机 械系统的数学建模过程中，粘性阻尼同样需要折算到某一部件上，求出系统的当量阻 尼系数。其基本方法是将摩擦阻力、流体阻力及负载阻力折算成与速度有关的粘性阻 尼力，再利用摩擦阻力与粘性阻尼力所消耗的功相等这一原则，求出粘性阻尼系数， 最后进行相应的当量阻尼系数折算。 在本例中工作台得摩擦损失占主导地位，其它各环节的摩擦损失相对而言可以忽 略不计。 当只考虑阻尼力时，根据工作台和丝杠之间动力关系有 T3 2 = cvL （2-16） 即丝杠旋转一周所做的功，等于工作台前进一个导程时其阻尼力所做的功。 根据力学原理和传动关系有 1 1 3 2 4 3 T z z z z T         = ，   2 1 2 4 1 3 L z z z z v         = 将以上两式代入式（2-16），并整理得 1 1 2 2 2 4 1 3 1 2    c c L z z z z T  =               = （2-17） 式中 c ——工作台导轨折算到轴 I 上的粘性阻尼系数 c L z z z z c 2 2 2 4 1 3 2                =  （2-18） 3 刚度系数的折算 机械系统中各元件在工作时受到力和/或力矩的作用，将产生伸长（或压缩）和/ 或扭转等弹性变形，这些变形将影响整个系统的精度和动态性能。在机械系统的数学 建模中，需要将其折算成相应的当量扭转刚度系数和/或线性刚度系数。 在本例中，首先将各轴的扭转角折算到轴 I 上，丝杠与工作台之间的轴向弹性变 形会使轴 III 产生一个附加扭转角，所以也要折算到轴 I 上，然后求出折算到轴 I 上的系统的当量刚度系数。 1）轴向刚度系数的折算 当系统受到载荷作用时，丝杠螺母副和螺母座都会产

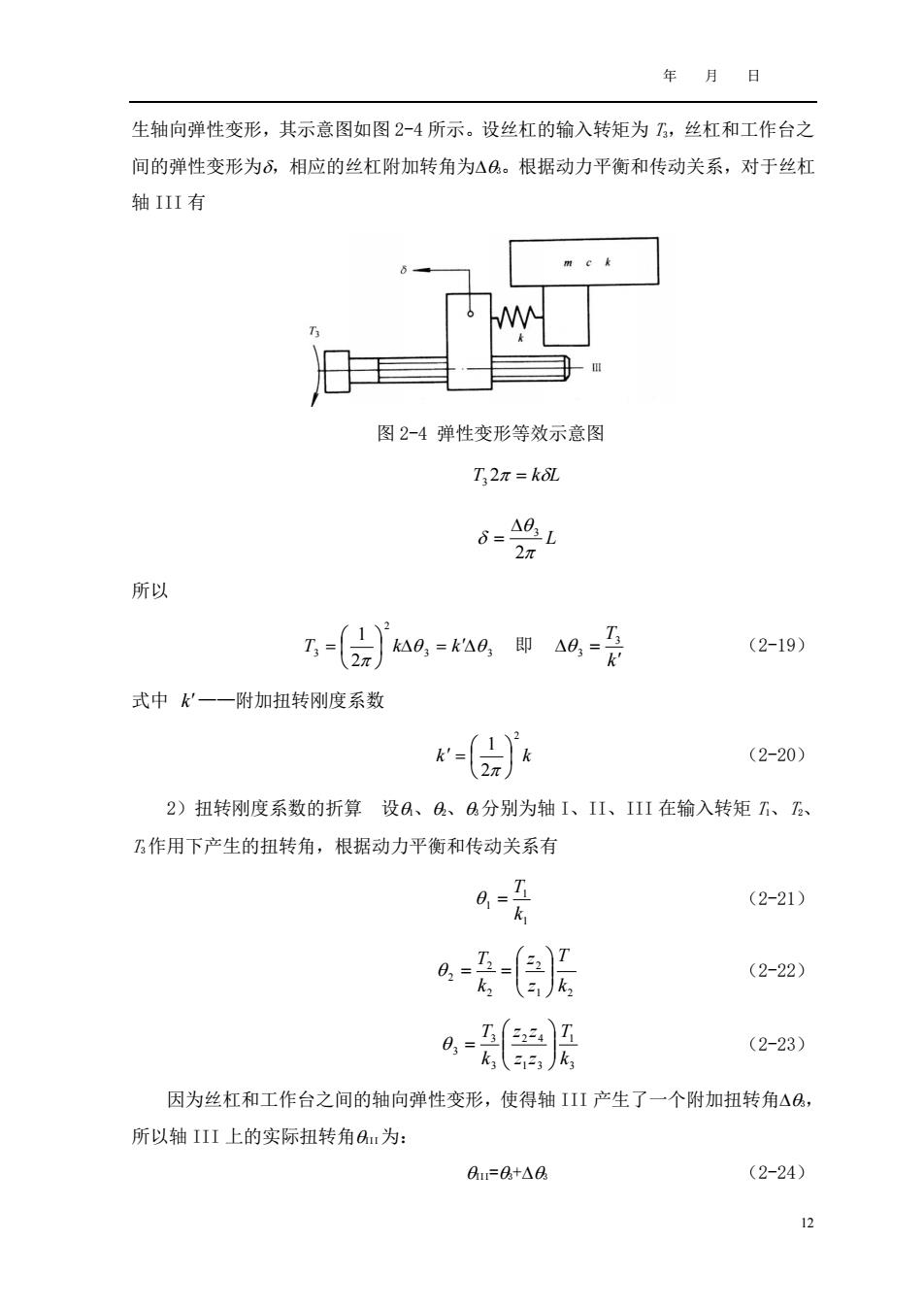
年月日 生轴向弹性变形，其示意图如图2-4所示。设丝杠的输入转矩为，丝杠和工作台之 间的弹性变形为d,相应的丝杠附加转角为△a。根据动力平衡和传动关系，对于丝杠 轴IIⅡ有 m e k 图2-4弹性变形等效示意图 T,2x=koL 6=A8L 27π 所以 万-(a0,=0,即ag-是 (2-19) 式中k一一附加扭转刚度系数 ( (2-20) 2)扭转刚度系数的折算设8、a、a分别为轴I、II、III在输入转矩T、、 万作用下产生的扭转角，根据动力平衡和传动关系有 a受 (2-21) a爱目 (2-22) 8- (2-23) 因为丝杠和工作台之间的轴向弹性变形，使得轴III产生了一个附加扭转角△a, 所以轴III上的实际扭转角A:为： a=a+△a (2-24) 12

年 月 日 12 生轴向弹性变形，其示意图如图 2-4 所示。设丝杠的输入转矩为 T3，丝杠和工作台之 间的弹性变形为，相应的丝杠附加转角为3。根据动力平衡和传动关系，对于丝杠 轴 III 有 图 2-4 弹性变形等效示意图 T3 2 = kL L    2  3 = 所以 3 3 2 3 2 1      =       T = k k 即 k T   = 3  3 （2-19） 式中 k——附加扭转刚度系数 k k 2 2 1        =  （2-20） 2）扭转刚度系数的折算 设1、2、3分别为轴 I、II、III 在输入转矩 T1、T2、 T3作用下产生的扭转角，根据动力平衡和传动关系有 1 1 1 k T  = （2-21） 1 2 2 2 2 2 k T z z k T          = = （2-22） 3 1 1 3 2 4 3 3 3 k T z z z z k T          = （2-23） 因为丝杠和工作台之间的轴向弹性变形，使得轴 III 产生了一个附加扭转角3， 所以轴 III 上的实际扭转角III为： III=3+3 （2-24）

年月日 将式(2-19)和式(2-21)代入式(2-22)得 a受++ (2-25) 将各轴的扭转角折算到轴I上，得到系统的当量扭转角 -8+自e- (2-26) 将式(2-21)、(2-22)和(2-23)代入式(2-25)得 偿 偶 (2-27) 式中T2一一折算到轴I上的当量扭转刚度系数 k= (2-28) 将基本物理量折算到某一部件后，即可按单一部件对系统进行建模。在本例中， 设输入量为轴I的转角x,输出量为工作台的线位移x,则可以得到数控机床进给系 统的数学模型 成+e成+x铝2x (2-29) 对应于该二阶线性微分方程的传递函数为 G)=七 ,22+cs+2(42m2+20.+a (2-30) 式中0，一一系统的固有频率，0，=√kΣ/J 5一一系统的阻尼比，5=/2√ks/J) 0,和5是二阶系统的两个特征参数，对于不同的系统可由不同的物理量确定， 3

年 月 日 13 将式（2-19）和式（2-21）代入式（2-22）得 III= 1 1 3 3 3 2 4 3 3 1 1 T z z k k z z k T k T          +         =  + （2-25） 将各轴的扭转角折算到轴 I 上，得到系统的当量扭转角             +         = + 1 3 2 4 2 1 2 1 z z z z z z III （2-26） 将式（2-21）、（2-22）和（2-23）代入式（2-25）得 1 3 2 1 3 2 4 2 1 2 1 2 1 1 1 1 T z z k k z z k T z z k T          +         +          = + 1 3 2 1 3 2 4 2 2 1 2 1 1 1 1 1 T z z k k z z z k z k                  +         +         = +  = T T1 （2-27） 式中 T ——折算到轴 I 上的当量扭转刚度系数          +         +         +  = z z k k z z z k z k k 1 1 1 1 1 3 2 1 3 2 4 2 2 1 2 1 （2-28） 将基本物理量折算到某一部件后，即可按单一部件对系统进行建模。在本例中， 设输入量为轴 I 的转角 xi，输出量为工作台的线位移 xo，则可以得到数控机床进给系 统的数学模型 o o o i k x L z z z z J x c x k x                  +  + = 2 4 2 1 3   （2-29） 对应于该二阶线性微分方程的传递函数为 ( ) ( ) ( ) 2 2 2 2 4 1 3 2 2 4 1 3 2 2 2 n n n i o s L z z z z J s c s k k L z z z z X s X s G s      + +         = +  +               = =    （2-30） 式中 n ——系统的固有频率， =   k J n  ——系统的阻尼比， ( )    = c / 2 k J n 和  是二阶系统的两个特征参数，对于不同的系统可由不同的物理量确定

月日 对于机械系统而言，它们是由质量、阻尼系数和刚度系数等结构参数决定的 第二节机械传动系统的特性 一、机电一体化对机械传动的要求 1、高精度 2、快速响应 3、良好的稳定性 二、机械传动系统的特性 转动惯量小摩擦小阻尼合适刚度大抗振性能好间隙小 转动惯量大会是机械负载增大、系统响应性能变慢、灵敏度降低、固有频率下降， 容易谐振。同时，使电气驱动部件谐振频率降低，阻尼增大。 阻尼越大，最大振幅越小，衰减越快。但定位精度降低，易产生爬行：稳态误差 大，精度降低。 刚度大，失动量小。提高刚度可增加闭环系统的稳定性。 第三节机械传动装置 一、齿轮传动 齿轮传动是应用非常广泛的一种机械传动，各种机床中传动装置几乎都离不开齿 轮传动。在数控机床伺服进给系统中采用齿轮传动装置的目的有两个，一是将高转速 低转矩的伺服电机（如步进电机、直流或交流伺服电机等）的输出，改变为低转速大 转矩的执行件的输出：另一是使滚珠丝杠和工作台的转动惯量在系统中占有较小的比 重。此外，对开环系统还可以保证所要求的精度。 提高传动精度的结构措施有： (一)适当提高零部件本身的精度： (二)合理设计传动链，减少零部件制造、装配误差对传动精度的影响 1、合理选择传动型式 2、合理确定级数和分配各级传动比 3、合理布置传动链

年 月 日 14 对于机械系统而言，它们是由质量、阻尼系数和刚度系数等结构参数决定的。 第二节 机械传动系统的特性 一、机电一体化对机械传动的要求 1、高精度 2、快速响应 3、良好的稳定性 二、机械传动系统的特性 转动惯量小 摩擦小 阻尼合适 刚度大 抗振性能好 间隙小 转动惯量大会是机械负载增大、系统响应性能变慢、灵敏度降低、固有频率下降， 容易谐振。同时，使电气驱动部件谐振频率降低，阻尼增大。 阻尼越大，最大振幅越小，衰减越快。但定位精度降低，易产生爬行；稳态误差 大，精度降低。 刚度大，失动量小。提高刚度可增加闭环系统的稳定性。 第三节 机械传动装置 一、齿轮传动 齿轮传动是应用非常广泛的一种机械传动，各种机床中传动装置几乎都离不开齿 轮传动。在数控机床伺服进给系统中采用齿轮传动装置的目的有两个，一是将高转速 低转矩的伺服电机（如步进电机、直流或交流伺服电机等）的输出，改变为低转速大 转矩的执行件的输出；另一是使滚珠丝杠和工作台的转动惯量在系统中占有较小的比 重。此外，对开环系统还可以保证所要求的精度。 提高传动精度的结构措施有： （一）适当提高零部件本身的精度； （二）合理设计传动链，减少零部件制造、装配误差对传动精度的影响 1、合理选择传动型式 2、合理确定级数和分配各级传动比 3、合理布置传动链

年月日 (三)采用消隙机构.以减少或消除空程。 由于数控设备进给系统经常处于自动变向状态，反向时如果驱动链中的齿轮等传 动副存在间隙，就会使进给运动的反向滞后于指令信号，从而影响其驱动精度。因此 必须采取措施消除齿轮传动中的间隙，以提高数控设备进给系统的驱动精度。 由于齿轮在制造中不可能达到理想齿面的要求，总是存在着一定的误差，因此两 个啮合着的齿轮，总应有微量的齿侧隙才能使齿轮正常地工作。以下介绍的几种消除 齿轮传动中侧隙的措施，都是在实践中行之有效的。 1.圆柱齿轮传动 (1)偏心轴套调整法 图2-5所示为简单的偏心轴套式消隙结构。电机1是通过偏心轴套2装到壳体上， 通过转动偏心轴套的转角，就能够方便地调整两啮合齿轮的中心距，从而消除了圆柱 齿轮正、反转时的齿侧隙。 图2-5偏心轴套式消除间隙结构 1-电动机2-偏心轴套 (2）锥度齿轮调整法 图2-6是用带有锥度的齿轮来消除间隙的机构。在加工齿轮1和2时，将假想的 分度圆柱面改变成带有小锥度的圆锥面，使其齿厚在齿轮的轴向稍有变化（其外形类 似于插齿刀)。装配时只要改变垫片3的厚度就能调整两个齿轮的轴向相对位置，从 而消除了齿侧间隙。但如增大圆锥面的角度，则将使啮合条件恶化

年 月 日 15 （三）采用消隙机构．以减少或消除空程。 由于数控设备进给系统经常处于自动变向状态，反向时如果驱动链中的齿轮等传 动副存在间隙，就会使进给运动的反向滞后于指令信号，从而影响其驱动精度。因此 必须采取措施消除齿轮传动中的间隙，以提高数控设备进给系统的驱动精度。 由于齿轮在制造中不可能达到理想齿面的要求，总是存在着一定的误差，因此两 个啮合着的齿轮，总应有微量的齿侧隙才能使齿轮正常地工作。以下介绍的几种消除 齿轮传动中侧隙的措施，都是在实践中行之有效的。 1. 圆柱齿轮传动 (1) 偏心轴套调整法 图 2-5 所示为简单的偏心轴套式消隙结构。电机 1 是通过偏心轴套 2 装到壳体上， 通过转动偏心轴套的转角，就能够方便地调整两啮合齿轮的中心距，从而消除了圆柱 齿轮正、反转时的齿侧隙。 图7-26 偏心轴套式消除间隙结构 1-电动机 2-偏心轴套 2 1 图 2-5 偏心轴套式消除间隙结构 1-电动机 2-偏心轴套 (2) 锥度齿轮调整法 图 2-6 是用带有锥度的齿轮来消除间隙的机构。在加工齿轮 1 和 2 时，将假想的 分度圆柱面改变成带有小锥度的圆锥面，使其齿厚在齿轮的轴向稍有变化（其外形类 似于插齿刀）。装配时只要改变垫片 3 的厚度就能调整两个齿轮的轴向相对位置，从 而消除了齿侧间隙。但如增大圆锥面的角度，则将使啮合条件恶化