
IH(jw)川(dB) 6(o) 0 180° -10 90° -20 w/Wc -30 0 0.010.11101001000 -40 -90° -50 W/Wc -60 -180° 0.0010.010.11 101001000 (a) (b) (c) 当F0时,20 log H(j@c)戶-3dB,我们说此高通滤波 电路的带宽从@到o。从图(c)可见,该高通滤波电路的相 移角度从90°到0°之间变化,当0o时,A=45°
当=C时,20log|H(jC )|=-3dB,我们说此高通滤波 电路的带宽从C 到∞。从图(c)可见,该高通滤波电路的相 移角度从90°到0°之间变化,当=C时,()=45 。 图 12-8
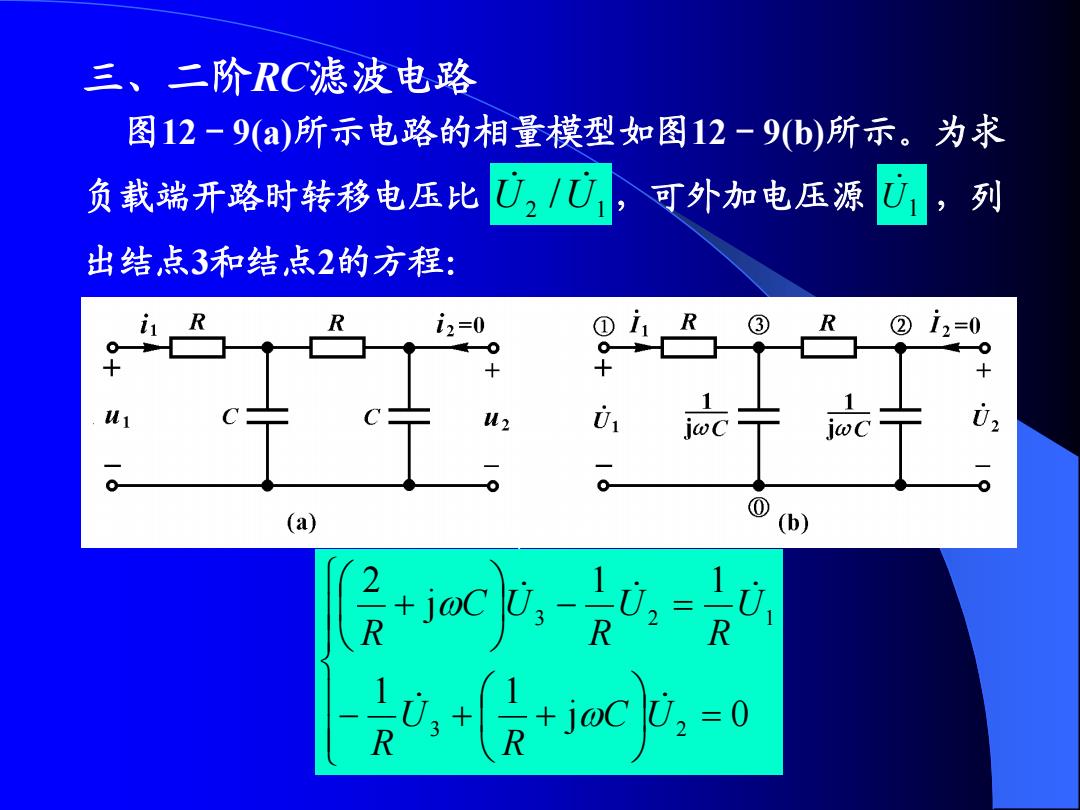
三、二阶RC滤波电路 图12-9(a)所示电路的相量模型如图12-9b)所示。为求 负载端开路时转移电压比U2/U) 可外加电压源 U,列 出结点3和结,点2的方程: R i2=0 ①i R ③ R ②i2=0 ui u2 01 02 (a) (b) 是,+后x-0
j 0 1 1 1 1 j 2 3 2 3 2 1 C U R U R U R U R C U R 图12-9(a)所示电路的相量模型如图12-9(b)所示。为求 负载端开路时转移电压比 ,可外加电压源 ,列 出结点3和结点2的方程: U1 2 1 U /U 图 12-9 三、二阶RC滤波电路
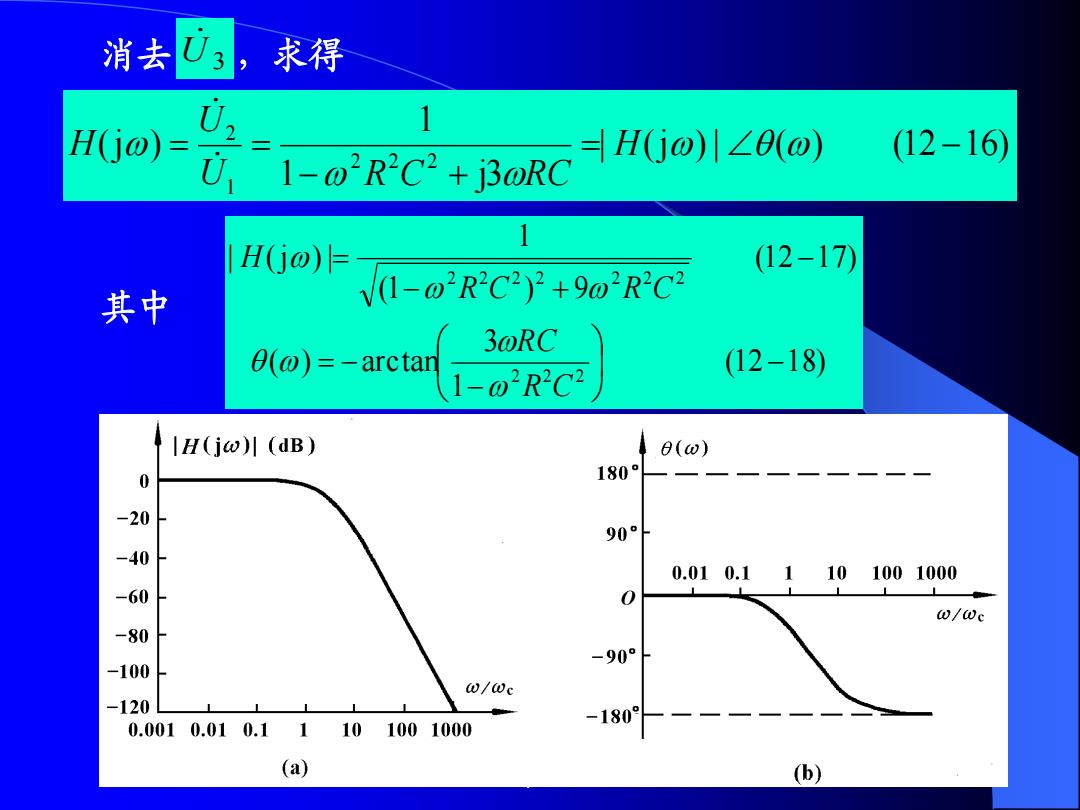
消去心, 求得 V H(j)= U HGo)川∠θ(o) (12-16 1-02R2C2+j3@RC H(jo)= (12-17) 其中 V1-o2R2C2)2+9o2R2C2 3@RC 0(@)=-arctan (12-18) 1-o2R2C2 IH(jw)川(dB) e(w) 0 180° -20 90 -40 0.010.11101001000 -60 0 0/0c -80 -90° -100 @/@c -120 0.0010.010.1110 1001000 -180° (a) (b)
消去 U 3 ,求得 | (j ) | ( ) (12 16) 1 j3 1 (j ) 2 2 2 1 2 H U R C R C U H 其中 (12 18) 1 3 ( ) arctan (12 17) (1 ) 9 1 | (j ) | 2 2 2 2 2 2 2 2 2 2 R C R C R C R C H 图 12-10

IH(jo川(dB) 6(o) 180 一 -20 90° -40 0.010.11 101001000 -60 0 w/Wc -80 -90 -100 w/Wc -120 0.0010.010.1110 1001000 -180° (a) (b) 该电路的幅频和相频特性曲线,如图所示。幅频曲线 表明该网络具有低通滤波特性,其转折频率0可令式(12 -17) H(jo) 0 求得 即 1-02R2C2)2+902R2C2=2 1 0.3742 求解得到 0c=1 (12-19) 2.6724RC T
该电路的幅频和相频特性曲线,如图所示。幅频曲线 表明该网络具有低通滤波特性,其转折频率C 可令式(12 -17) 0.707 求得 2 1 | H(jω )| 即 (1 ) 9 2 2 2 2 C 2 2 2 2 C R C R C 求解得到 (12 19) 0.3742 2.6724 1 C R C
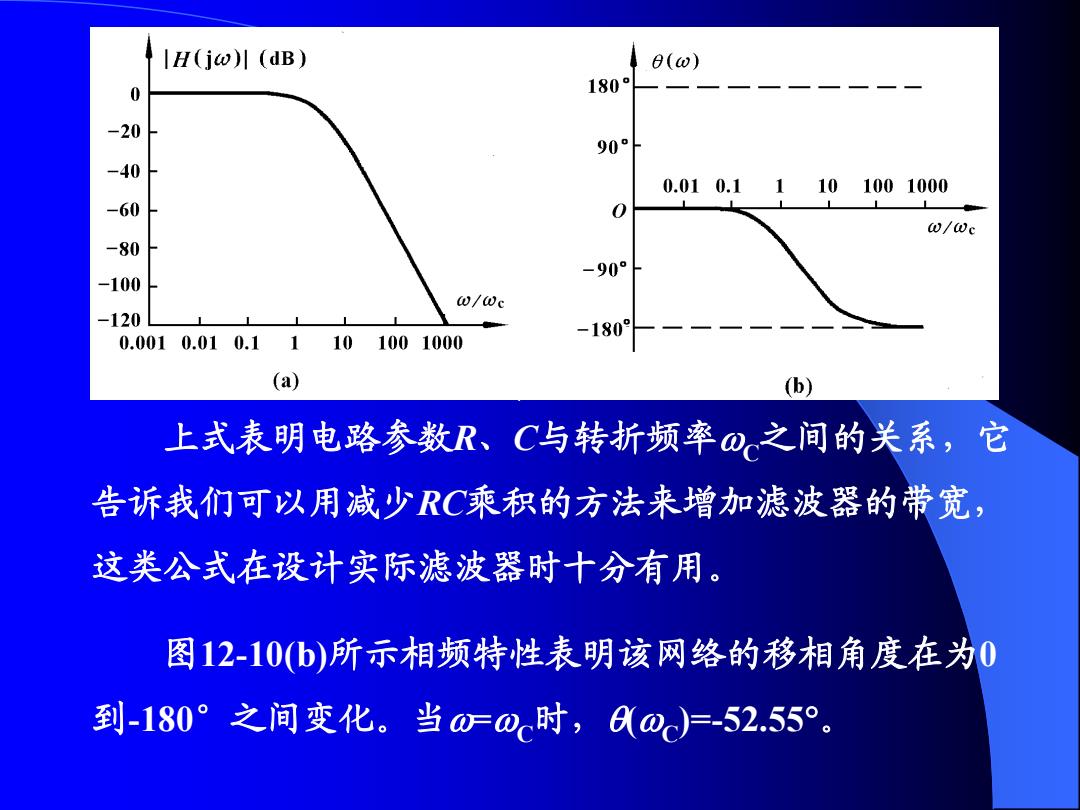
IH(jw)川(dB) e(w) 0 180 -20 90 -40 0.010.11101001000 -60 0 w/We -80 -90° -100 w/@c -120 0.0010.010.11101001000 -180 (a) (b) 上式表明电路参数R、C与转折频率⊙之间的关系,它 告诉我们可以用减少RC乘积的方法来增加滤波器的带宽, 这类公式在设计实际滤波器时十分有用。 图12-10(b)所示相频特性表明该网络的移相角度在为0 到-180°之间变化。当00时,0)尸-52.55°
上式表明电路参数R、C与转折频率C之间的关系,它 告诉我们可以用减少RC乘积的方法来增加滤波器的带宽, 这类公式在设计实际滤波器时十分有用。 图12-10(b)所示相频特性表明该网络的移相角度在为0 到-180°之间变化。当=C时,(C )=-52.55 。 图 12-10