
ME6011弹性塑性力学 主讲:胡永祥博士 办公室:机械A楼708 电话:021-34206554 13564691365 Email huyx@sjtu.edu.cn A 制瞳蚊术写膜膏自财化研克所 圈秋峰 ME6011弹性塑性力学 第1章应力分析 应力状态 。三维应力状态分析 三维应力状态的主应力 9 最大剪应力 等倾面上的正应力和剪应力 9 应力张量的分解 平衡微分方程 圆海人座 ME6011弹性塑性力学 1
1 ME6011 弹性塑性力学 ME6011 弹性塑性力学 主 讲:胡永祥 博士 办公室:机械A楼708 电 话:021-34206554 13564691365 Email :huyx@sjtu.edu.cn 制造技术与装备自动化研究所 ME6011 弹性塑性力学 第1章 应力分析 应力状态 三维应力状态分析 三维应力状态的主应力 最大剪应力 等倾面上的正应力和剪应力 应力张量的分解 平衡微分方程 2
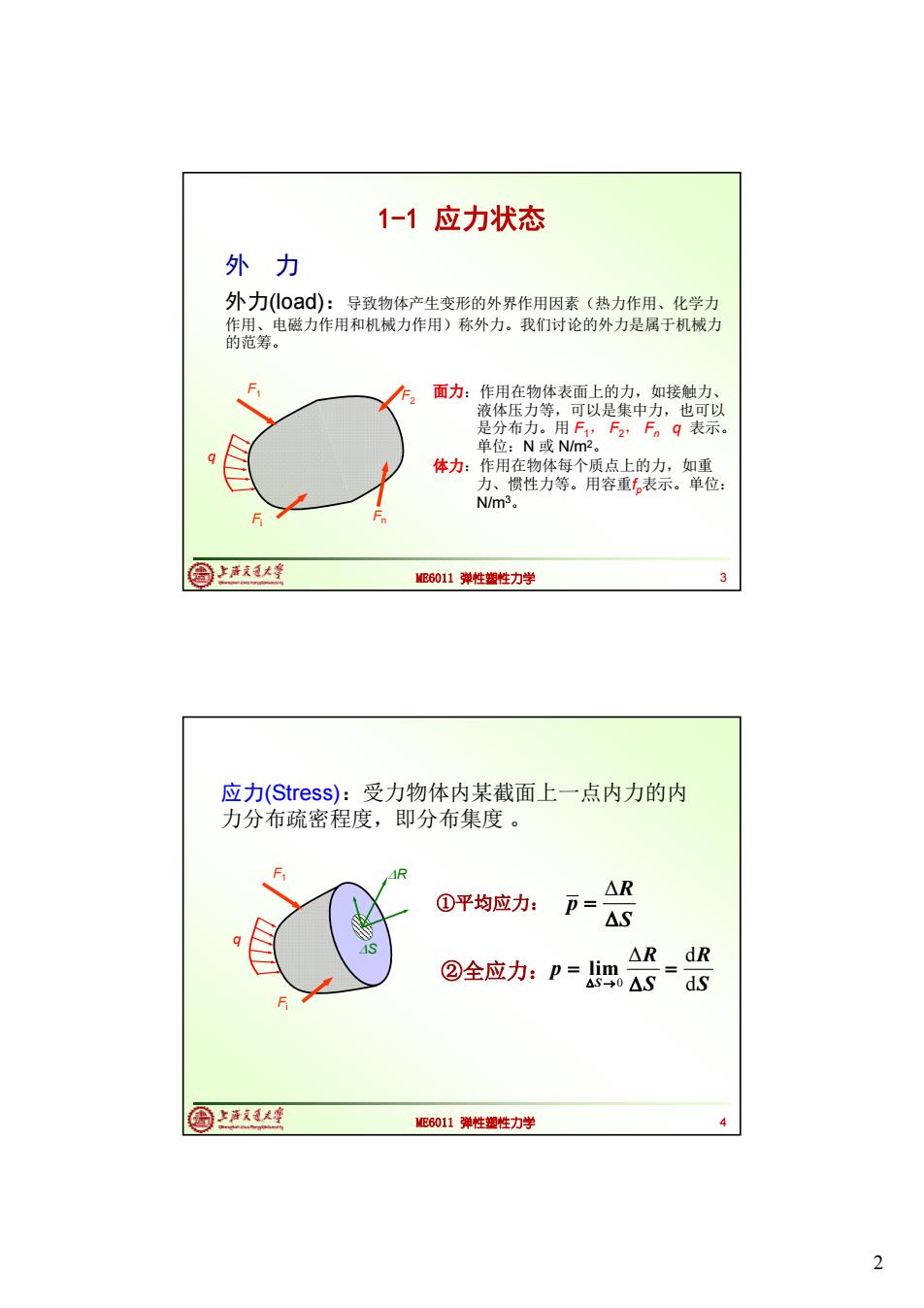
1-1应力状态 外力 外力(0ad):导致物体产生变形的外界作用因素(热力作用、化学力 作用、电磁力作用和机械力作用)称外力。我们讨论的外力是属于机械力 的范筹。 面力:作用在物体表面上的力,如接触力、 液体压力等,可以是集中力,也可以 是分布力。用F,F2,Fnq表示。 单位:N或N/m2。 体力:作用在物体每个质点上的力,如重 力、惯性力等。用容重表示。单位: N/m3。 F 周上我人 ME6011弹性塑性力学 应力(Stress):受力物体内某截面上一点内力的内 力分布疏密程度,即分布集度。 △R ①平均应力: p= △S ②全应力:p=im AR dR 4s→0△S ds 圆上1大峰 ME6011弹性塑性力学 2
2 ME6011 弹性塑性力学 外 力 外力(load):导致物体产生变形的外界作用因素(热力作用、化学力 作用、电磁力作用和机械力作用)称外力。我们讨论的外力是属于机械力 的范筹。 F1 Fi F2 Fn q 面力:作用在物体表面上的力,如接触力、 液体压力等,可以是集中力,也可以 是分布力。用 F1, F2, Fn q 表示。 单位:N 或 N/m2。 体力:作用在物体每个质点上的力,如重 力、惯性力等。用容重fp表示。单位: N/m3。 1-1 应力状态 3 ME6011 弹性塑性力学 应力(Stress):受力物体内某截面上一点内力的内 力分布疏密程度,即分布集度 。 ①平均应力: ②全应力: ΔR p S 0 Δ d d lim S R R p S S F1 Fi R q S 4

应力分解: 某截面外法线方向为n, 微面上应力p称为全应力(stress), n可分解为正应力(normal sress)g和 剪应力(shear stress)Tm △R 垂直于截面的应力称为“正应力”: dR o lim= s0△S ds lim △R dR. 位于截面内的应力称为“剪应力”: △S-→0△S ds MB6011弹性塑性力学 一维问题: φ=0 轴向拉伸的等截面直杆,截面积S 0=0,t=0 4 o=2,=2 横截面 中= 平面假设→σ均匀分布 2 0,=0,t,=0 0=S t=0 y斜截面 P P 全应力p= = =o cos S/cosp 正应力o,=pcosp=ocos2p 剪应力t,=psinp=osinpcosp @认峰 ME6011弹性塑性力学 3
3 ME6011 弹性塑性力学 应力分解: 0 Δ d Δ d lim n n n S R R S S Δ 0 Δ d Δ d n lim S R R S S 垂直于截面的应力称为“正应力”: 位于截面内的应力称为“剪应力”: F1 Fi p q n n 某截面外法线方向为 n n, 微面上应力p 称为全应力(stress) , n可分解为正应力(normal sress) n和 剪应力(shear stress) n 5 ME6011 弹性塑性力学 一维问题: 轴向拉伸的等截面直杆,截面积S 横截面 , 0 S P 平面假设→σ均匀分布 斜截面 cos cos S P S P 全应力 p 2 正应力 p cos cos 剪应力 p sin sin cos P P p 0 4 2 6 , 0 , 2 2 0, 0

二维问题:平面应力状态分析 静力平衡 方程 sin o 斜截面法向o.S=(o,Scos)cos中+(o,Ssin)sinp +(Scos)sin+(Ssin)cos 斜截面切向t·S=(o,Scos)sin-(o,Ssin)cos中 +(Ssin)sin-(Scos)cos 圆上活庆大等 ME6011弹性塑性力学 φ斜截面上的应力: a=2o,+o,)+2a.-,)cos20+7msin20 1 (,-,)sin 20-t cos2 消去φ 一-2a,+o,P+r=a.-o,护+r 4 主平面方位(x=0): (Ox,U) tan 2o = 2tg 0x-0y 0 主应力大小: (y,T) 应力圆 0+02± 02 最大剪应力:大小与方位 圆上1大峰 ME6011弹性塑性力学 4
4 ME6011 弹性塑性力学 x y xy x y xy S S cos S sin 静力平衡 方程 斜截面法向 斜截面切向 S ( cos ) cos ( sin ) sin ( cos ) sin ( sin ) cos x y xy xy S S S S S ( cos ) sin ( sin ) cos ( sin ) sin ( cos ) cos x y xy xy S S S S 7 二维问题: 平面应力状态分析 ME6011 弹性塑性力学 ( ) cos 2 sin 2 2 1 ( ) 2 1 x y x y xy φ斜截面上的应力: 消去φ 2 2 2 2 ( ) 4 1 ( )] 2 1 [ x y x y xy ( , ) x xy ( , ) y yx o 0 2 主平面方位( =0): 1 ( ) sin 2 cos 2 2 x y xy 2 1 主应力大小: x y xy 2 tan 2 0 2 2 2 1 ) 2 ( 2 xy x y x y 应力圆 8 最大剪应力:大小与方位
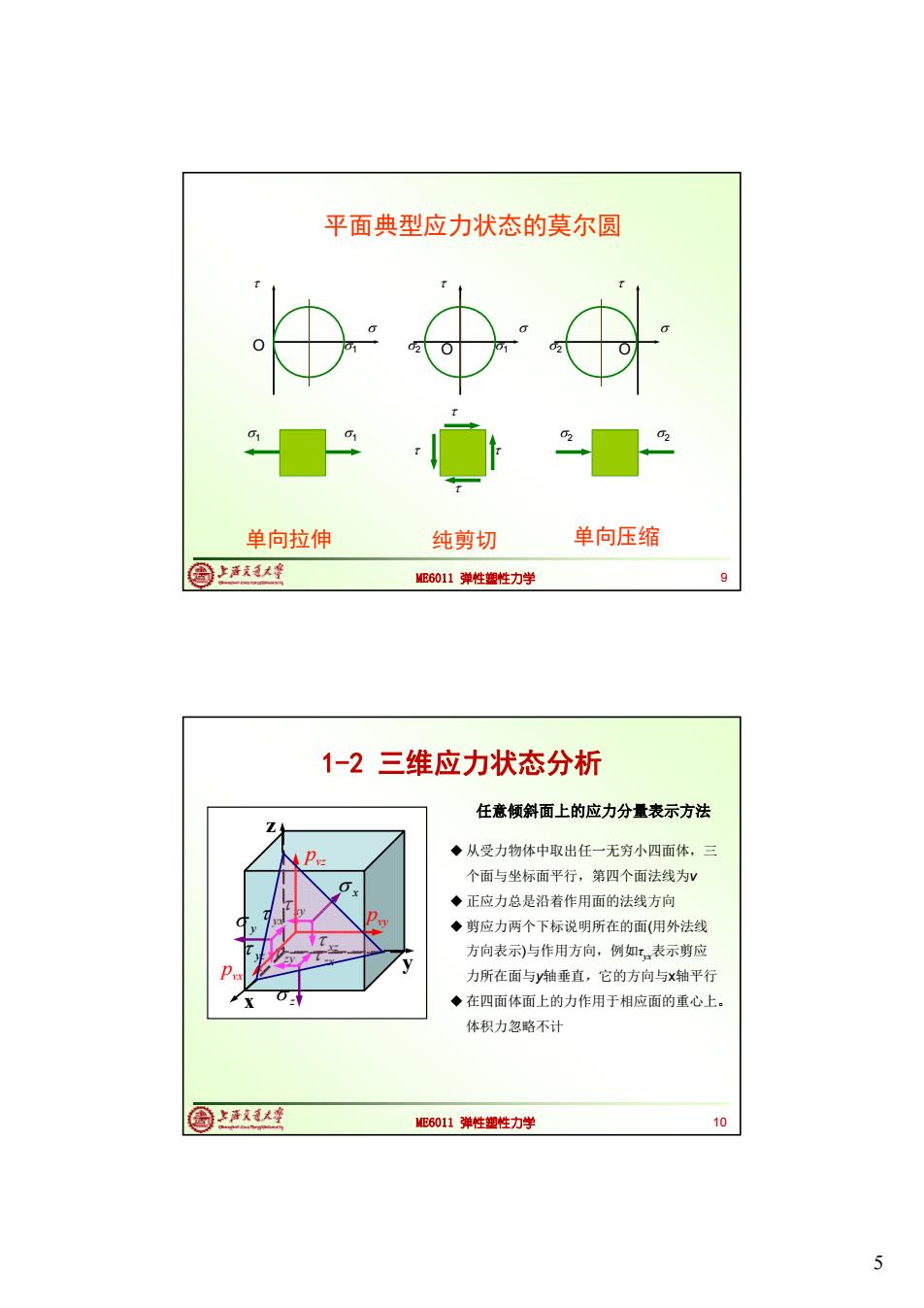
平面典型应力状态的莫尔圆 单向拉伸 纯剪切 单向压缩 圈上清式大等 ME6011弹性塑性力学 9 1-2三维应力状态分析 任意倾斜面上的应力分量表示方法 ◆从受力物体中取出任一无穷小四面体,三 个面与坐标面平行,第四个面法线为V ◆正应力总是沿着作用面的法线方向 ◆剪应力两个下标说明所在的面(用外法线 方向表示)与作用方向,例如表示剪应 力所在面与y轴垂直,它的方向与x轴平行 ◆在四面体面上的力作用于相应面的重心上。 体积力忽略不计 圆上1大峰 ME6011弹性塑性力学 10 5
5 ME6011 弹性塑性力学 O 1 2 O 1 2 O 1 1 2 2 单向拉伸 纯剪切 单向压缩 平面典型应力状态的莫尔圆 9 ME6011 弹性塑性力学 1-2 三维应力状态分析 y z x yz xz xy zy yx zx y x z vx p pvy vz p 10 任意倾斜面上的应力分量表示方法 从受力物体中取出任一无穷小四面体,三 个面与坐标面平行,第四个面法线为v 正应力总是沿着作用面的法线方向 剪应力两个下标说明所在的面(用外法线 方向表示)与作用方向,例如τyx表示剪应 力所在面与y轴垂直,它的方向与x轴平行 在四面体面上的力作用于相应面的重心上。 体积力忽略不计