输入: 100点 ←49个零点 一51点 28个零点 第一段 0(P-1) 4849 (Q) 99100 127 100点 28个零点 第二段 -49点- 51点 (P) (Q) 输出 二49点一51点→2点 二9点.一51点→二:28点 图P4-12

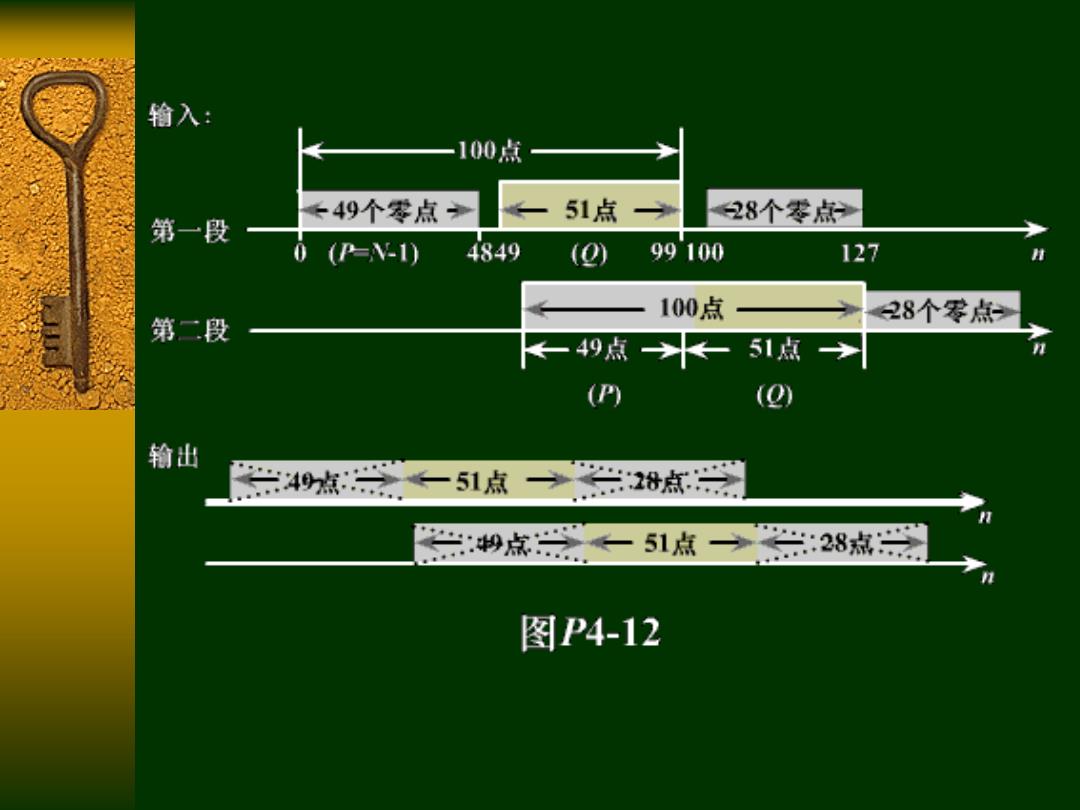
(a)由于用重叠保留法,如果冲激响应h(n)的点数为 N点,则圆周卷积结果的前面的N-1个点不代表线性 卷积结果,故每段重叠点数P为 P=W-1=50-1=49 (b)每段点数为27=128,但其中只有100个点是有效输 入数据,其余28个点为补充的零值点。因而各段不重 叠而又有效的点数Q为 2=100-P=100-49=51 (c)每段128个数据点中,取出来的Q个点的序号从 n=49到n=99。用这些点和前后段取出的相应点连接 起来,即可得到原来的长输入序列。 另外,对于第一段数据没有前一段,故在数据之前必 须加上P=N-1=49个零值点,以免丢失数据
解:(a)由于用重叠保留法,如果冲激响应 h n 的点数为 N点,则圆周卷积结果的前面的 N 1 个点不代表线性 卷积结果,故每段重叠点数P为 P N 1 50 1 49 (b)每段点数为 7 2 128 ,但其中只有100个点是有效输 入数据,其余28个点为补充的零值点。因而各段不重 叠而又有效的点数Q为 Q P 100 100 49 51 (c)每段128个数据点中,取出来的Q个点的序号从 n 49 到 n 99 。用这些点和前后段取出的相应点连接 起来,即可得到原来的长输入序列。 另外,对于第一段数据没有前一段,故在数据之前必 须加上 P N 1 49 个零值点,以免丢失数据

第五章习题讲解
第五章习题讲解

、用直接I型及典范结构实现以下系统函数: H() 3+4.2z1+0.8z2 2+0.621-0.4z2 解:根据IIR滤波器的系统函数标准式 M H(2)=m=0 Y() 1-∑ ”X) n 将系统函数整理为: H() 1.5+2.1z+0.4z2 1.5+2.1z1+0.4z2 1+0.3z-0.2:21-(0.3z+0.2z2)
1、用直接I型及典范结构实现以下系统函数: 1 2 1 2 3 4.2 0.8 2 0.6 0.4 z z H z z z = 解:根据IIR滤波器的系统函数标准式 1 2 1 2 1.5 2.1 0.4 1 0.3 0.2 z z H z z z = 将系统函数整理为: 0 1 1 M m m m N n n n b z Y z H z X z a z = 1 2 1 2 1.5 2.1 0.4 1 0.3 0.2 z z z z

1.5+2.1z1+0.4z2 H(z)= 1-(-0.3z1+0.2z2) 得a1=-0.3,a2=02b=1.5,b=2.1,b2=0.4 x(n) 1.5 ()) 直接I型结构: 2.1 -0.3 0.4 0.2 图P5-1(a) 典范型结构:x 1.5 y(n) -0.3 21 0.2 0.4
1 a 0.3 2 得 , a 0.2 0 b 1.5 1 b 2.1 2 , , b 0.4 直接I型结构: 典范型结构: 1 2 1 2 1.5 2.1 0.4 ( ) 1 0.3 0.2 z z H z z z