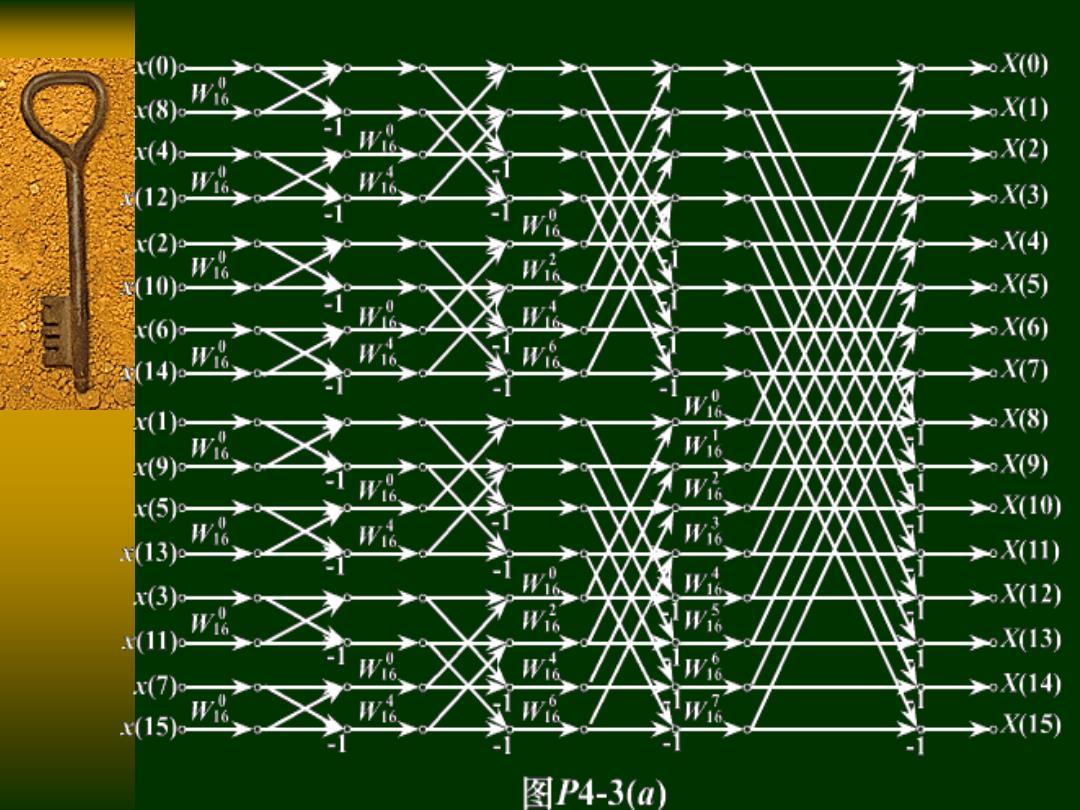
X0) X(1) 4 X(2) 12 >X(3) X(4) 10 →X(5) X(6) >X(7 →X(8) →X(9) (5 →X(10) 13) oX(11) >X(12) 11) →X(13) >X(14) x(15) X(15) 图P4-3(a)

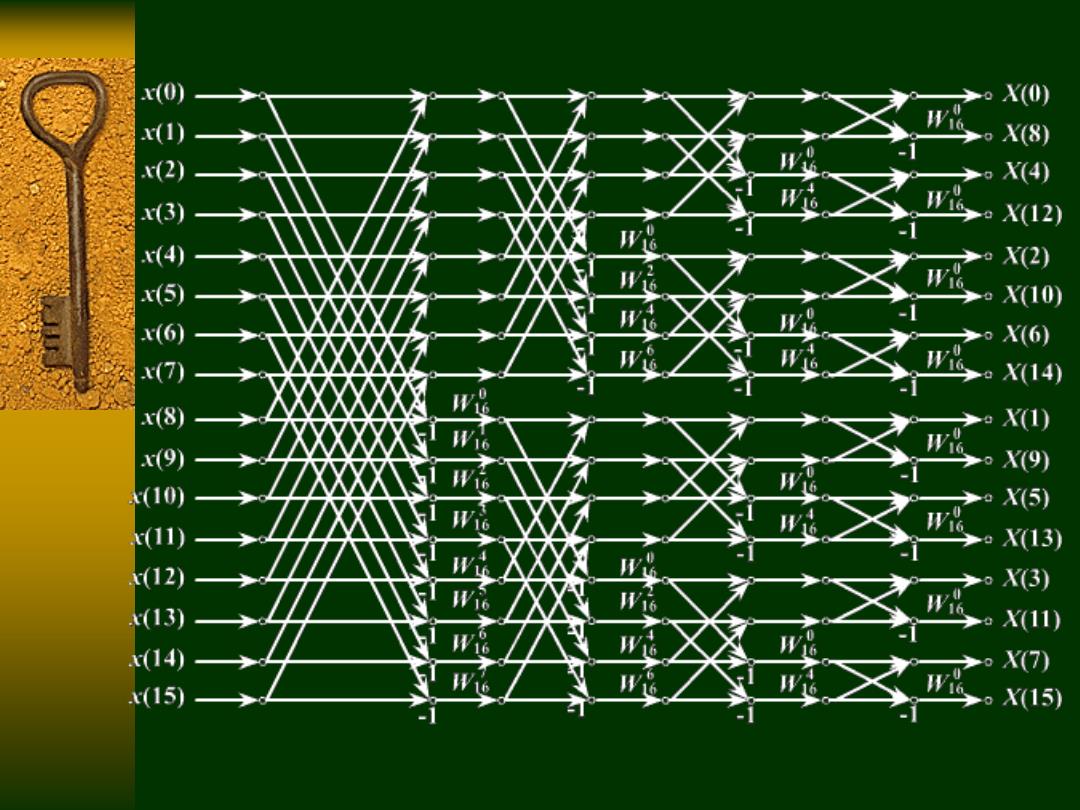
2)按频率抽取的基-2F℉T流图 同样共有L=4级蝶形运算,每级N/2=8个蝶形运算 基本蝶形是DIT蝶形的转置 X(k) X(k) Xm-() -1 X.(i) 每个蝶形的两节点距离为2-”,即从第一级到 第四级两节点距离分别为8,4,2,1。 系数WW的确定:r=(K)2·2m- 即的二进制左移m-1位补零
(2) 按频率抽取的基-2FFT流图 基本蝶形是DIT 蝶形的转置 同样共有L = 4级蝶形运算,每级N / 2 = 8个蝶形运算 每个蝶形的两节点距离为 ,即从第一级到 第四级两节点距离分别为8,4,2,1。 2 L m 1 2 ( ) 2 1 r m W r k N k m 系数 的确定: 即 的二进制左移 位补零 r WN 1 ( ) X k m 1 ( ) X j m ( ) X k m ( ) X j m -1
0 X(0) 6 X(8) X(4) 高三 X(12) 6 X(2) X(10) 16 X(6) X(14) X(1) X(9) X(5) X13) W X3) 6 6 X(11) X(7) X15)

N=16 直接计算DFT需要N2=256次复数乘法 N(N-1)=240次复数加法 利用FFT计算需要。log2N=32次复数乘法 N1og2N=64次复数加法 若不计乘±1及乘±的运算量 则实际乘法次数为10次复数乘法
若不计乘 及乘 的运算量 1 j 则实际乘法次数为10次复数乘法 2 16 DFT 256 ( -1) 240 N N N N 直接计算 需要 次复数乘法 次复数加法 2 2 FFT log 32 2 log 64 N N N N 利用 计算需要 次复数乘法 次复数加法

13.我们希望利用一个单位抽样响应点数N=50的有 限冲激响应滤波器来过滤一串很长的数据。要求利用 重叠保留法通过快速傅里叶变换来实现这种滤波器, 为了做到这一点,则: (1)输入各段必须重叠P个抽样点; (2)我们必须从每一段产生的输出中取出Q个抽样 点,使这些从每一段得到的抽样连接在一起时,得到 的序列就是所要求的滤波输出。假设输入的各段长度 为100个抽样点,而离散傅里叶变换的长度为128点。 进一步假设,圆周卷积的输出序列标号是从n=0到 n=127,则 (a) 求P; (b)求Q; (©)求取出来的Q个点的起点和终点的标号,即确定从 圆周卷积的128点中要取出哪些点,去和前一段的点衔 接起来
13. 我们希望利用一个单位抽样响应点数N = 50 的有 限冲激响应滤波器来过滤一串很长的数据。要求利用 重叠保留法通过快速傅里叶变换来实现这种滤波器, 为了做到这一点,则: (1)输入各段必须重叠P个抽样点; (2)我们必须从每一段产生的输出中取出Q个抽样 点,使这些从每一段得到的抽样连接在一起时,得到 的序列就是所要求的滤波输出。假设输入的各段长度 为100个抽样点,而离散傅里叶变换的长度为128点。 进一步假设,圆周卷积的输出序列标号是从 n = 0到 n = 127,则 (a)求P; (b)求Q; (c)求取出来的Q个点的起点和终点的标号,即确定从 圆周卷积的128点中要取出哪些点,去和前一段的点衔 接起来