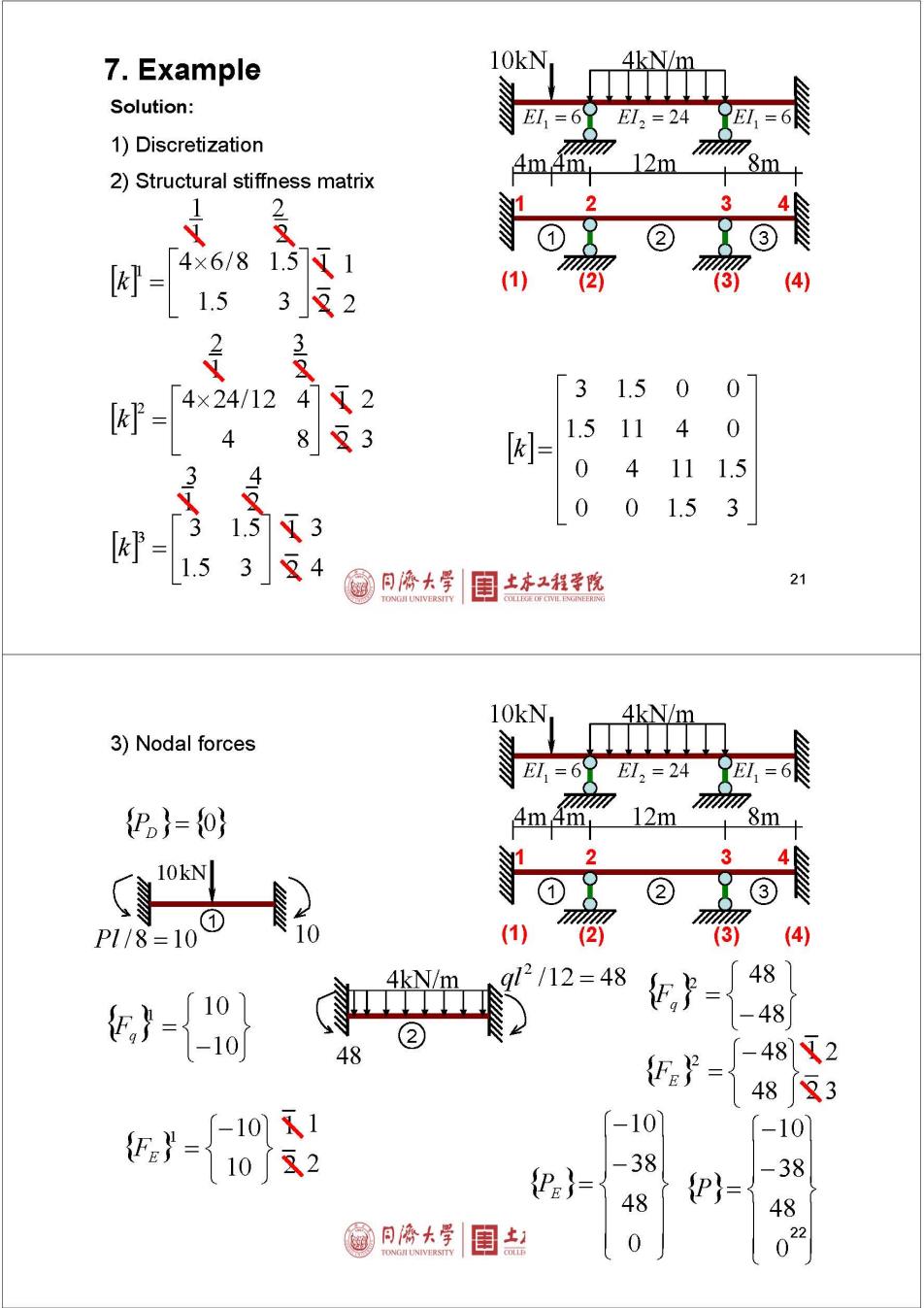
7.Example 10kN 4kN/m Solution: E以=6 EI2=24 EI 6 1)Discretization 4m4m 12m 8m 2)Structural stiffness matrix 2 2 3 ① 2 [k= 4×6/81.5 1 (1) 2 4) 1.5 3 2 3 4×24/12 4 2 3 1.5 0 0 4 83 1.5 11 4 0 [= 3 4 0 4 11 1.5 0 0 1.5 3 = 1.5 3 15 3 4 同©大学 土本工程学院 21 10kN 4kN/m 3)Nodal forces = EI2=24 EL 6 {Po}=0} 4m4m 12m 8m 1 2 3 10kN ① ② (3 ① P1/8=10 10 (1) (2) 3) (4) 4kN/m gl2/12=48 48 g- } -48 ② 48 482 483 医-S -10 -10 Pa)= -38 -38 48 P)= 4 同除大经 0 02

10kN 4kN/m 4)Boundary condition 1.50 -10 E,=6 EI2=24 EI 6 5 11 4 38 12m 8m 4 11 5 48 4m4m 1.5 0 2 3 ① 2 3 0 0 0 0 2 0 11 (1) 4 0 62 38 4) 0 4 11 0 48 0 64 0 6)Member end forces 0 0 5)solve the equation 0 5.81 1.29 4}= 62 6.476 -27.43 0 同源大学 目 土本2程学院 23 10kN 4kN/m E,=6 EI,=24 6 F 8 4-5.81,「 48 27.43 4m4m 12m 8m 4 86.476-48 -19.43 3 1.56.476 19.43 1 2 3 F) 30o ① ② 1.5 9.71 (1) (2) (3) (4) 7)Moment diagram 2743-19.43 9.71 同©大学 土本工程学院 24
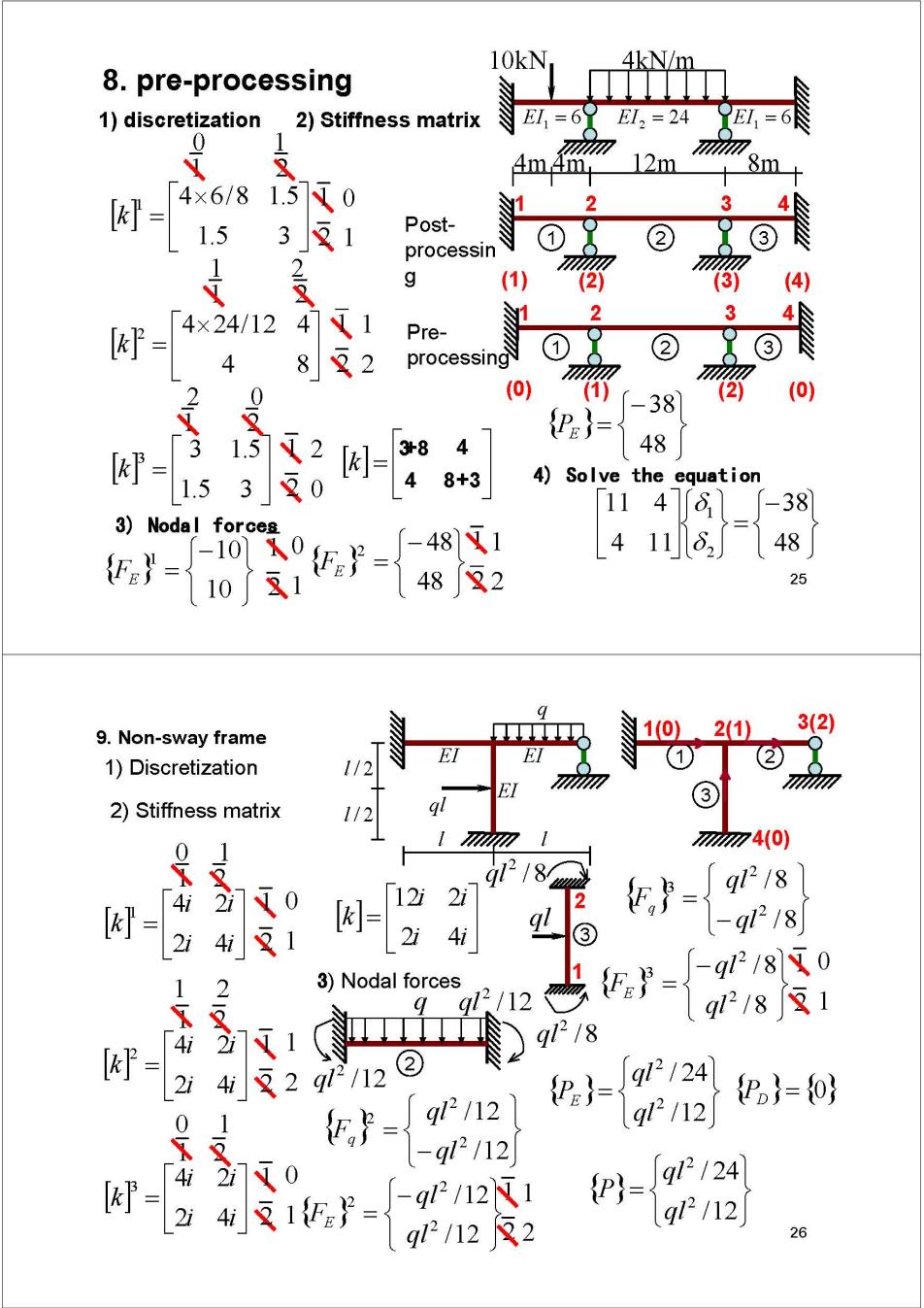
10kN 4kN/m 8.pre-processing 1)discretization 2)Stiffness matrix E,=6 EI2=24 6 4m4m 12m 8m [= 4×6/8 1.50 2 3 1.5 3反1 Post- ① ② 3 processin 是 Nlot g (1) 21 2 3 = 4×24/12 4]N1 Pre- 4 82 cess7no义 ② 0 (0) -38 (2) (0) 3 1.5 2 4 {P= 48 4)Solve the equation 11 46 38 3)Nodal forces - =-01 4 1182 48 25 9.Non-sway frame 1(0) 2(1) 3(2) 1)Discretization ① 2 ③ 2)Stiffness matrix 1/2 74(0) 12 gl2/8 「4i 0 12i gl218 会 3)Nodal forces gl2/12 -{8X0 q218s1 = 4i 1 q1218 q212A Pn}={o} ,= gl2/121 g/12 -q2/12 0 2 ief-B - 26

qf/8买 1(0)、2(1) 3(2) 4)Solve the equation 1/2 EI ① ③ Z4() 图-w 臂州阳 5)Member end forces -8 18 -10 -gf18 同濟大学 目 土本工程学院 27 13.3 planar frames 1.Discretization (6 5(13,14,15 6(16,17,18 Coordinate system: ② global local 3(7,8,9) 4(10,11,12 ④ 1 2 (1,2,3) (4,5,6) X Curve->straight Tapered->uniform 同©大学 土本工程学院 28
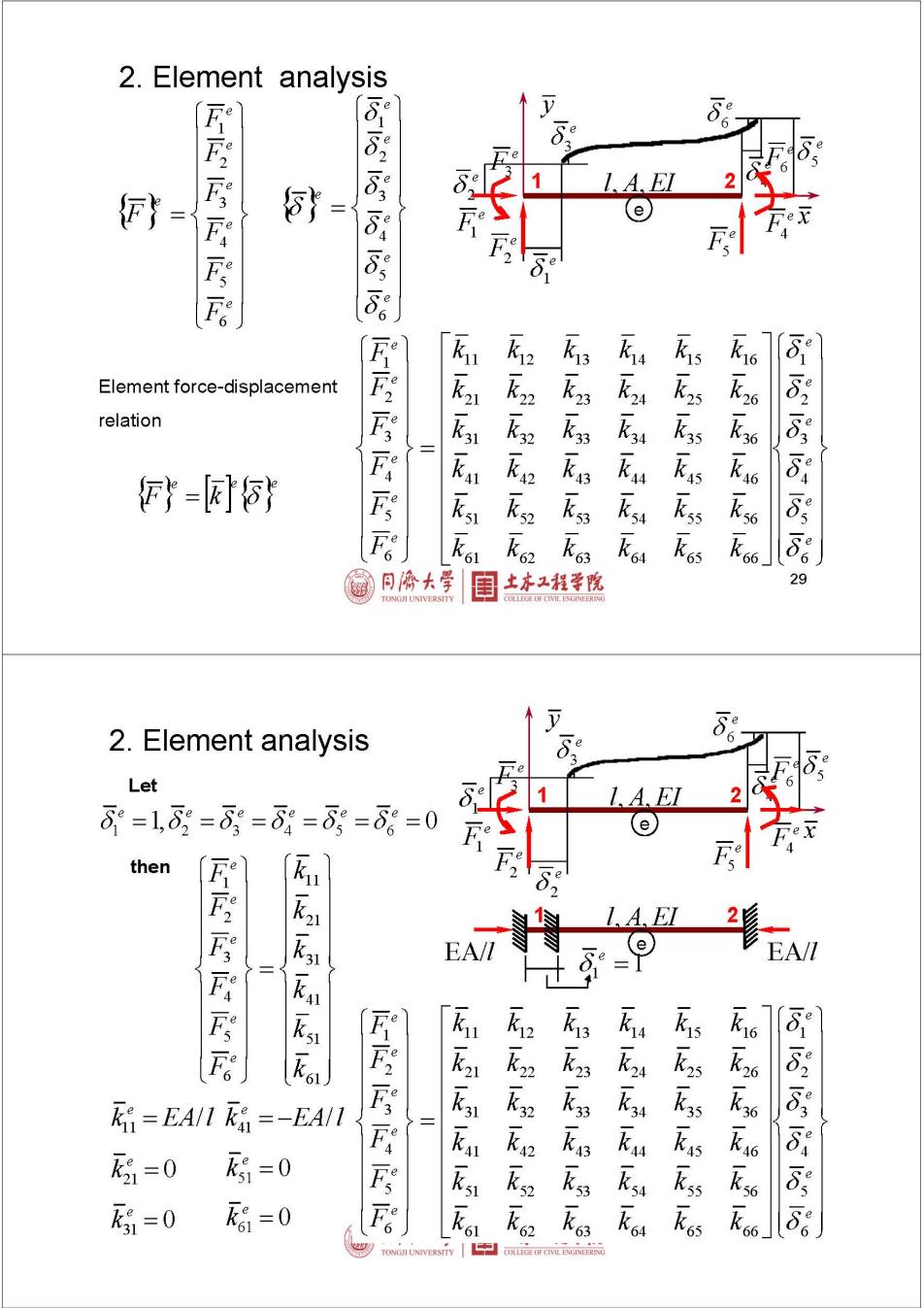
2.Element analysis δ 安 1.A.EI F}- Element force-displacement relation F}=财 月大学 目 土本工程学院 29 2.Element analysis Let 1.A.EI 8e=l,6=8=δ=8=6 9=0 e then 一一一 L.A.EI 2 EA/I EA/I 无41 k=EA/I ki =-EA/I 所=0 不3=0 系一系一系系一系福 不51=0 后=0