
解:DE=VAE2+ADz=V5. 当△AED∽△CMN时,AE:CM=DE:MN, 即1:CM=V5:1,酵得CM=5, 5 当△AED∽△CNM时,AD:CM=DE:MN, 即2:CM=V5:1,解得CM2 · 所以当CM=5或25时, 5 △AED与以M,N,C为项点的三角形相似. 合
解:DE= 𝐀𝐄 𝟐 + 𝐀𝐃𝟐 = 𝟓. 当△AED∽△CMN 时,AE∶CM=DE∶MN, 即 1∶CM= 𝟓∶1,解得 CM= 𝟓 𝟓 ; 当△AED∽△CNM 时,AD∶CM=DE∶MN, 即 2∶CM= 𝟓∶1,解得 CM=𝟐 𝟓 𝟓 . 所以当 CM= 𝟓 𝟓 或 𝟐 𝟓 𝟓 时, △AED 与以 M,N,C 为顶点的三角形相似
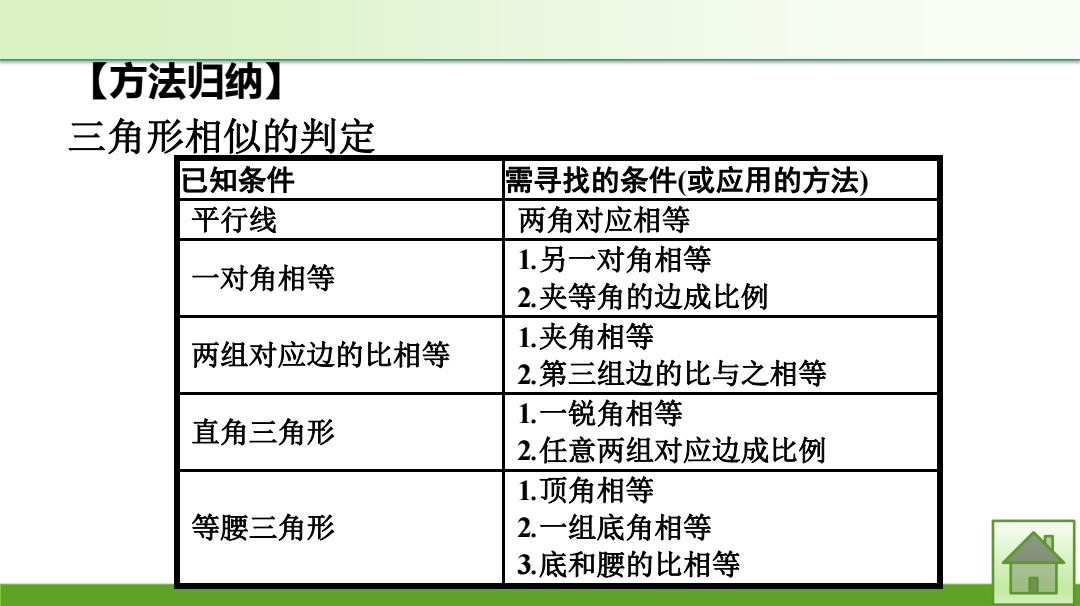
方法归纳】 三角形相似的判定 已知条件 需寻找的条件(或应用的方法) 平行线 两角对应相等 1.另一对角相等 一对角相等 2.夹等角的边成比例 两组对应边的比相等 1夹角相等 2.第三组边的比与之相等 直角三角形 1.一锐角相等 2.任意两组对应边成比例 1.顶角相等 等腰三角形 2.一组底角相等 3.底和腰的比相等
【方法归纳】 三角形相似的判定 已知条件 需寻找的条件(或应用的方法) 平行线 两角对应相等 一对角相等 1.另一对角相等 2.夹等角的边成比例 两组对应边的比相等 1.夹角相等 2.第三组边的比与之相等 直角三角形 1.一锐角相等 2.任意两组对应边成比例 等腰三角形 1.顶角相等 2.一组底角相等 3.底和腰的比相等