
§2分配问题与匈牙利法 例2有一份中文说明书,需译成英、日、德、俄四 种文字。现有甲、乙、丙、丁四人,他们将中文说 明书译成不同语种的说明书所需时间如下表所示, 问如何分派任务,可使总时间最少? 人员 甲 任务 乙 丙 丁 英 2 10 9 7 日 15 4 14 8 德 13 14 16 11 俄 4 15 13 9 2014-12-15 11
2014-12-15 11 §2 分配问题与匈牙利法 例2 有一份中文说明书,需译成英、日、德、俄四 种文字。现有甲、乙、丙、丁四人,他们将中文说 明书译成不同语种的说明书所需时间如下表所示, 问如何分派任务,可使总时间最少? 人员 任务 甲 乙 丙 丁 英 2 10 9 7 日 15 4 14 8 德 13 14 16 11 俄 4 15 13 9
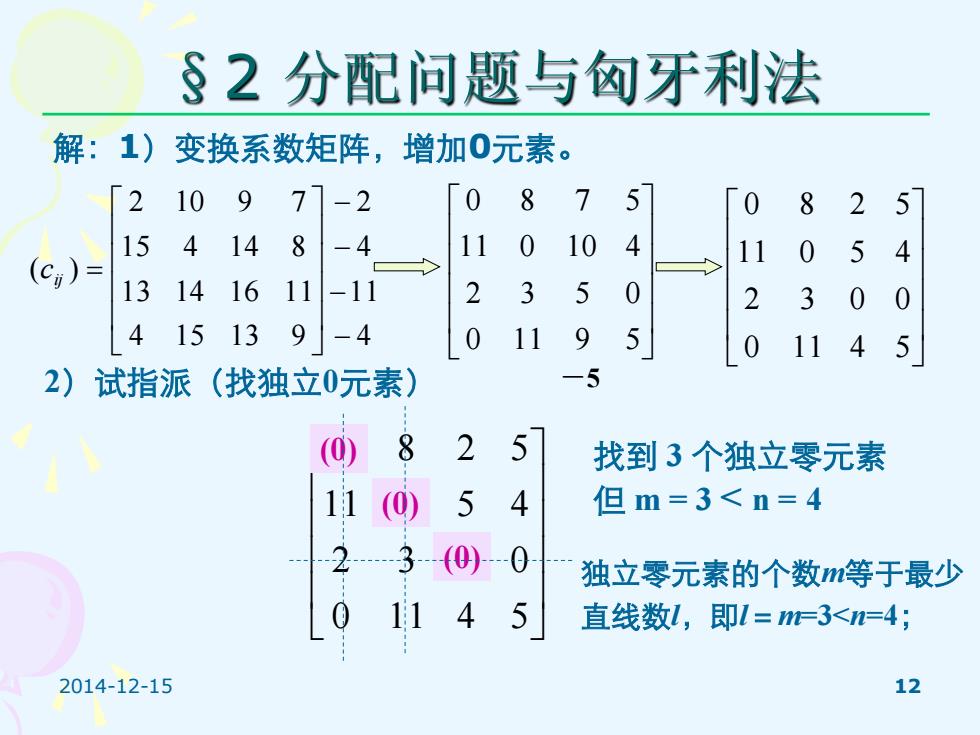
§2分配问题与匈牙利法 解:1) 变换系数矩阵,增加0元素。 2 10 9 71-2 0 8 7 5 0 8 2 5 15 14 8 -4 11 0 10 4 11 0 5 4 (c)= 13 14 16 11 -11 2 3 5 0 2 3 0 0 4 15 13 -4 9 0 11 9 5 0 11 4 5 2)试指派 (找独立0元素) -5 (@ 8 2 5 找到3个独立零元素 11 (0) 5 4 但m=3<n=4 2.3-0)-0 独立零元素的个数m等于最少 11 4 直线数l,即l==3<n=4; 2014-12-15 12
2014-12-15 12 §2 分配问题与匈牙利法 解:1)变换系数矩阵,增加0元素。 0 11 4 5 2 3 0 0 11 0 5 4 0 8 2 5 4 11 4 2 4 15 13 9 13 14 16 11 15 4 14 8 2 10 9 7 ( ) cij 0 11 9 5 2 3 5 0 11 0 10 4 0 8 7 5 2)试指派(找独立0元素) -5 找到 3 个独立零元素 但 m = 3 < n = 4 0 11 4 5 2 3 0 0 11 0 5 4 (0) 0 8 2 5 (0) (0) 独立零元素的个数m等于最少 直线数l,即l=m=3<n=4;

§2分配问题与匈牙利法 3)没有被直线通过的元素中选择最小值为2,变换系数矩 阵,将没有被直线通过的所有元素减去这个最小元素;直 线交点处的元素加上这个最小值。得到新的矩阵,重复2) 步进行试指派 2014-12-15 13
2014-12-15 13 §2 分配问题与匈牙利法 3)没有被直线通过的元素中选择最小值为2,变换系数矩 阵,将没有被直线通过的所有元素减去这个最小元素;直 线交点处的元素加上这个最小值。得到新的矩阵,重复2) 步进行试指派
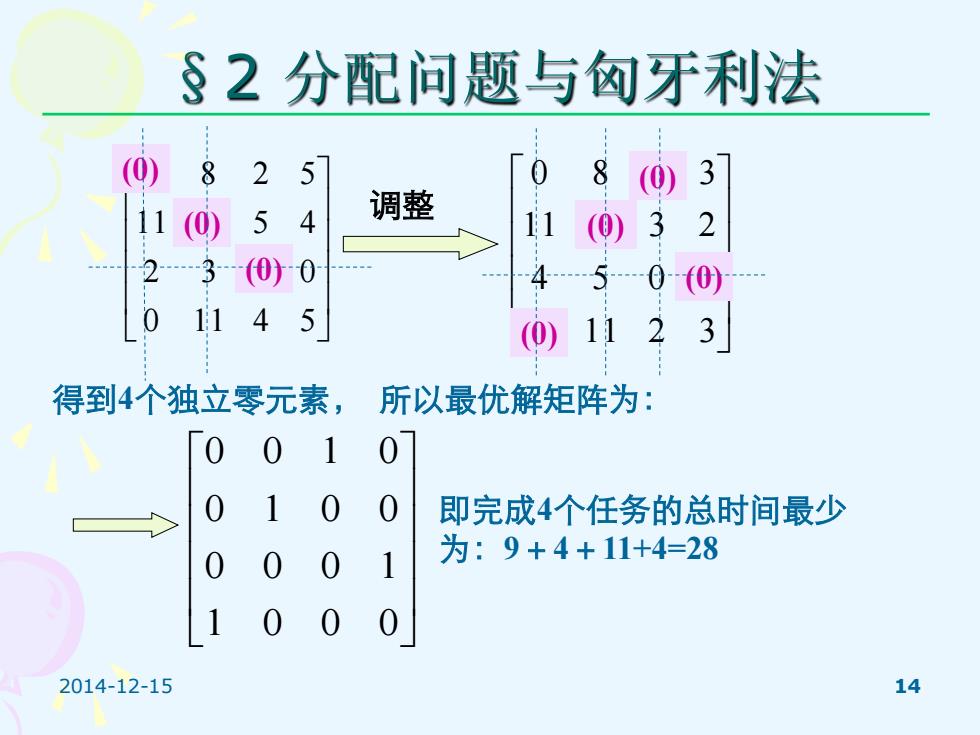
§2分配问题与匈牙利法 (0) 8 2 5 8 (0) 3 11 (0) 5 4 调整 11(0) 3 2 2.3 (00 4.5.00) 0 11 45 (0) 112 3 得到4个独立零元素, 所以最优解矩阵为: 0 0 1 0 0 1 0 即完成4个任务的总时间最少 0 0 0 为:9+4+11+4=28 1 0 0 0 2014-12-15 14
2014-12-15 14 §2 分配问题与匈牙利法 0 11 4 5 2 3 0 0 11 0 5 4 0 8 2 5 调整 0 11 2 3 4 5 0 0 11 0 3 2 0 8 0 3 (0) (0) 得到4个独立零元素, 所以最优解矩阵为: 1 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0 即完成4个任务的总时间最少 为:9+4+11+4=28 (0) (0) (0) (0) (0)
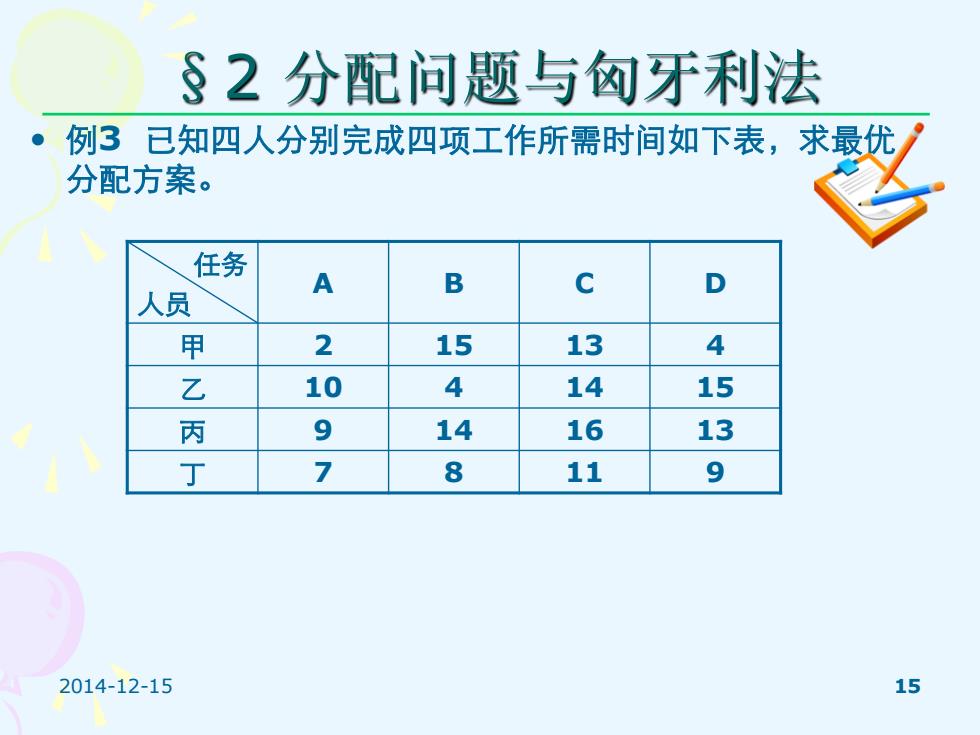
§2分配问题与匈牙利法 ● 例3已知四人分别完成四项工作所需时间如下表,求最优 分配方案。 任务 A B D 人员 甲 2 15 13 4 乙 10 4 14 15 丙 9 14 16 13 丁 7 8 11 9 2014-12-15 15
2014-12-15 15 §2 分配问题与匈牙利法 • 例3 已知四人分别完成四项工作所需时间如下表,求最优 分配方案。 任务 人员 A B C D 甲 2 15 13 4 乙 10 4 14 15 丙 9 14 16 13 丁 7 8 11 9