
§2分配问题与匈牙利法 指派问题的数学模型的标准形式: 设n个人被分配去做件工作,规定每个人只做一件工作, 每件工作只有一个人去做。已知第个人去做第j件工作的效率 (时间或费用)为C=1.2.nj=1.2.n)并假设Ci≥0。问应 如何分配才能使总效率(时间或费用)最高? 设决策变量 1 指派第个人做第件事 0 不指派第个人做第件事 (i,j=1,2,.,n) 2014-12-15 6
2014-12-15 6 §2 分配问题与匈牙利法 指派问题的数学模型的标准形式: 设n 个人被分配去做n 件工作,规定每个人只做一件工作, 每件工作只有一个人去做。已知第i个人去做第j 件工作的效率 ( 时间或费用)为Cij(i=1.2.n;j=1.2.n)并假设Cij ≥0。问应 如何分配才能使总效率( 时间或费用)最高? 设决策变量 ( , 1,2,., ) 0 i j 1 i j xi j i j n 不指派第个人做第件 事 指派第 个人做第件 事

§2分配问题与匈牙利法 指派问题的数学模型为: minZ=会2cx, 2=1=12.n 2,=10=12.m x取0或1(i,i=1.2.n) 2014-12-15
2014-12-15 7 §2 分配问题与匈牙利法 指派问题的数学模型为: 0 1( , 1.2. . ) 1 ( 1.2. . ) 1 ( 1.2. . ) min 1 1 1 1 x i j n x j n x i n Z c x i j n i i j n j i j n i n j i j i j 取 或

§2分配问题与匈牙利法 匈牙利解法: 标准的指派问题是一类特殊的0-1整数规划问题,可以用 多种相应的解法来求解。但是,这些方法都没有充分利用指 派问题的特殊性质来有效减少计算量。1955年,库恩 (W.W.Kuhn)利用匈牙利数学家克尼格(D.Konig)的关于 矩阵中独立零元素的定理,提出了指派问题的一种解法,由 此,习惯上称之为匈牙利解法。 2014-12-15 8
2014-12-15 8 §2 分配问题与匈牙利法 匈牙利解法: 标准的指派问题是一类特殊的 0-1 整数规划问题,可以用 多种相应的解法来求解。但是,这些方法都没有充分利用指 派问题的特殊性质来有效减少计算量。1955年,库恩 (W.W.Kuhn)利用匈牙利数学家克尼格(D.König)的关于 矩阵中独立零元素的定理,提出了指派问题的一种解法,由 此,习惯上称之为匈牙利解法

§2分配问题与匈牙利法 克尼格定理: 定理1:如果从分配问题效率矩阵[Q]的每一行元素中分别 减去(或加上)一个常数U,从每一列中分别减去(或加上)一 个常数y,得到一个新的效率矩阵bJ,则以[b]为效率矩 阵的分配问题与以[Q]为效率矩阵的分配问题具有相同的 最优解。 定理2:若矩阵A的元素可分为“0”元和“非0”元,则覆盖 “0”元的最少直线数等于位于不同行、不同列的“0”元的最 大个数。 2014-12-15
2014-12-15 9 §2 分配问题与匈牙利法 克尼格定理 : 定理1:如果从分配问题效率矩阵[aij]的每一行元素中分别 减去(或加上)一个常数ui,从每一列中分别减去(或加上)一 个常数vj,得到一个新的效率矩阵[bij],则以[bij]为效率矩 阵的分配问题与以[aij]为效率矩阵的分配问题具有相同的 最优解。 定理2:若矩阵A的元素可分为“0”元和“非0”元,则覆盖 “0”元的最少直线数等于位于不同行、不同列的“0”元的最 大个数
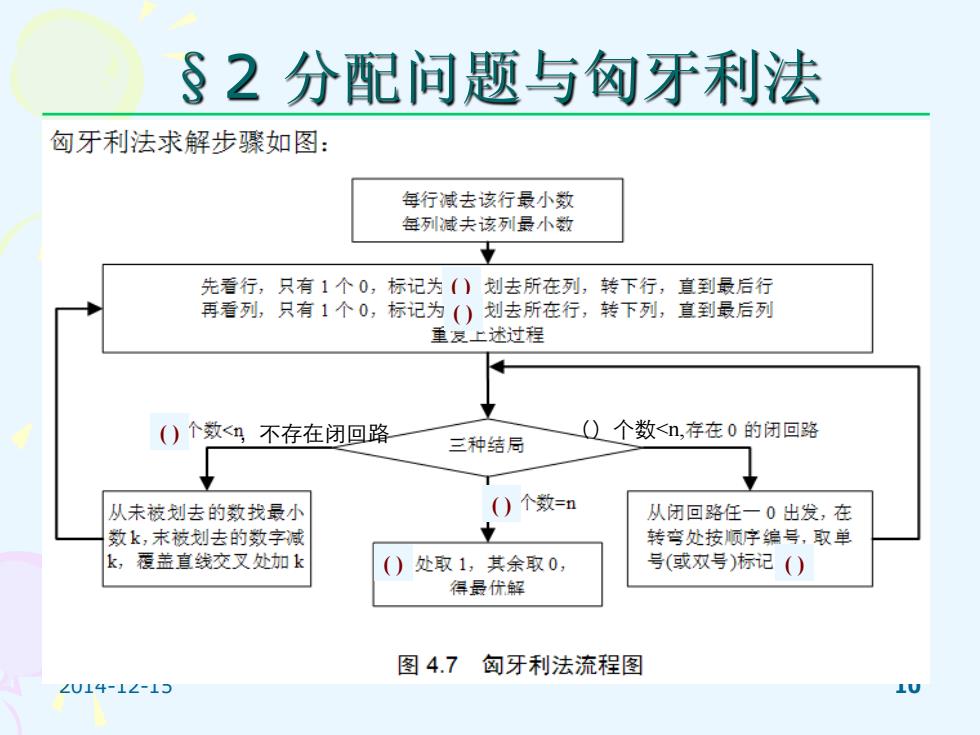
§2分配问题与匈牙利法 匈牙利法求解步骤如图: 每行减去该行最小数 每列减夫该列最小数 五 先看行,只有1个0,标记为()划去所在列,转下行,直到最后行 再看列,只有1个0,标记为()划去所在行, 转下列,直到最后列 重发上述过程 ()个数<马不存在闭回路 三种结局 ()个数<n,存在0的闭回路 从未被划去的数找最小 ()个数=n 从闭回路任一0出发,在 数k,末被划去的数字减 转弯处按顺序编号,取单 k, 履盖直线交叉处加k ()处取1,其余取0, 号(或双号)标记() 得最优解 图4.7匈牙利法流程图 ∠U14-1∠-13 LU
2014-12-15 10 §2 分配问题与匈牙利法 ( ) ( ) ( ) ( ) ( ) ( ) ,不存在闭回路 ()个数<n