
式中A,仙,p分别称为振幅、角颜率和初相,均为实常数。 若A,“,不为常数,则分别称为变幅度的、变频率的、变相位的正弦信号,或者称调幅的、 调频的、调相的正弦信号。 正弦信号有如下性质: (1)其微分仍然是正弦信号,即 品fe)=品[Acos(a+p]=Acos[w+p+】 可见仅是幅度增至如倍,初相增加了艺。 (2)满足如下形式的二阶微分方程,即 ()=o 在信号与系统分析中,这一性质非常有用。 3.单位阶跃信号 11(>0) -侵t-0) 0a<0) 4,单位冲激信号 (1)定义: j-i oo)dt=1 (2)性质: f(t)8(t)=f(0)8(t) f(e)8(t-6)=f()8(t-to) ∫fe)8e灿=fo) ∫fe)8e-d=f,) 6(t)=8(-t) 6-)=8[-(t-)] ia)=是i) 8(at-a) ∫fe)8ard=fo) ∫'fa8a-wa= 0-e 8(r)dr =U() 2

式中a为大于圣的实常数:为实常数。 5.单位冲激偶信号() (1)定义: (2)性质: 8(t)=-8(-t) 8(t-to)=-8[-(u-] 广0r=0[四)为商西数] ∫n8(edr=ie) f(u)8(e)=f(0)8e)-P(0)8(a) f(t)8(t-to)=f(to)8(t-t)-f(t)8(t-) ∫fe8e0d=-Po) [f(t)8u-t)dt =-P(t) f(t)8(t-t)dt=(-1)f(to) 式中t。为实常数。 6.杆号画数sgn() f1(t0) gna)=0=o) {-1(t<0) 或 sgn(e)=U(e)-U(-t)=2U()-1 7.单位斛坡信号 单位斜坡信号r()与U(),6()的关系: r()=U(rdr 2-ve rw=广广edr d'ru)=8(t) 8.单边表减指数信号f)=AeU(e)=Ae-Ur) 式中口,r均为>0的实常数,r四合称为时间常数,单位为s,当:-「=合时有 f(x)=Ae1=0.368A 9.复指数信号 f(t)Ae* (-∞<1<十∞) 式中5=g十jo称为复颜率:0,u均为实常数,c的单位为l/s,w的单位为rad/s (1)当5=0时,ft)=A,为直流信号: (2)当s=a时,J(:)=Ae,为实指数信号: 一3

(3)当s=jw时,f(e)=Ae"=Acos(at)+jAsin(a): ()当s=g+jm时,/e)=Ae[cos(r)+jsin(e)]. 10.抽样信号 f)=i=Sa(0)(-<<+o) 其性质如下: (1)f)-sint为实变量t的偶函数: (2)limgf()f(0)-lim sin (3)当t=kx(k=士1,士2,士3,.)时,f)=0: 6)m-0. 1.1.3信号的时域分解 (1)任意信号(:)可分解为在不同时刻阶跃的具有不同阶跃幅度的无穷多个阶跃函数的 连缕和,即 f0=广frUu-r0dr≈2-kar)ar )任意信号(:)可分解为在不同时刻出现的具有不同强度的无穷多个冲激函数的连续 和,即 f)-J广fra-rdr≈之f△r)8-arar (3)信号f(:)可分解为直流分量fn)与交流分量f()之和,即 f(t)-fn(t)+f() (4)信号f()可分解为偶分量∫()与奇分量(t)之和,即 f)=f.()+fo(t) 式中/)=U)+f(-)]:(0=2f)-f-)]。 若f)为因果信号,则有 .(t)=。(t) (>0) f()=-fat)(t<0) 或写成 手,(t)=f(t)sgn(t) (t)=f.(1)sgn(t) 1.1,4信号的时域变换 (I)折叠:将信号f()以纵坐标轴为轴折叠,即得折叠信号f(一t).将∫()中的t换以 (一),所得f(-t)为f()的折叠信号。 (2)时移:将信号f()沿t轴平移:即得时移信号f(1一x),x为实常数,当π>0时为右 移,当t<0时为左移,信号时移用时移器(也称延时器)实现,如图1.1所示。 (3)倒(反)相:将信号f()以横坐标轴(即1轴)为轴翻转180°,即得倒相(反相)信号 [-f()门,用倒相器实现,如图1.2所示。 (4)时域展缩:以变量at置换f(u)中的变量t,即得展缩信号f(at),a为非零正实#数,若 0<a<1,则表示f(:)的被形在时间轴上展宽到原来的1/a倍,如图1.3(b)所示(a取):若
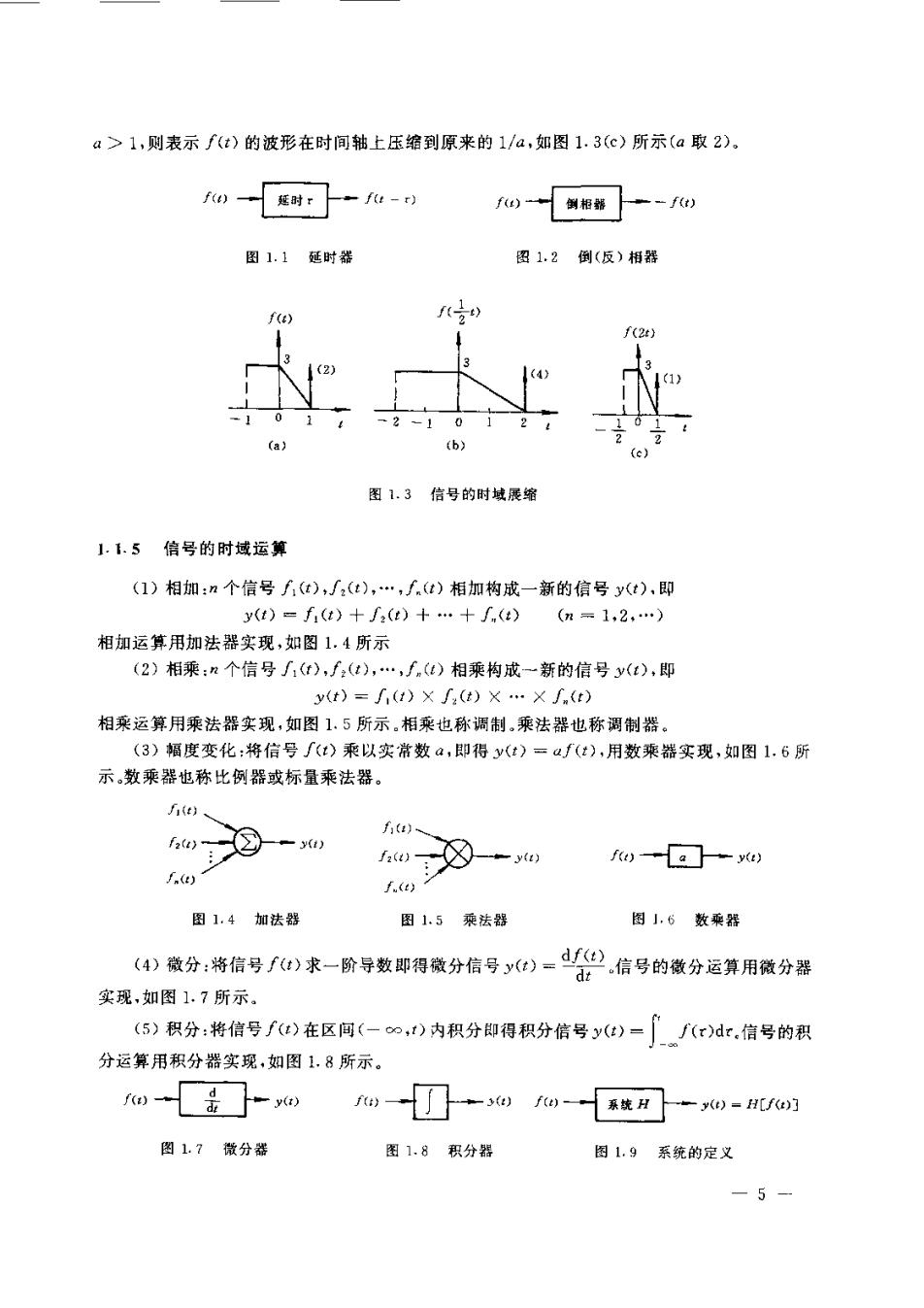
a>1,则表示f(t)的波形在时间轴上压缩到原来的1/a,如图1.3(c)所示(a取2), 0一时门-)心一制阳蒂一- 图1.1延时恭 图1.2倒(反)相器 f20 0 图1.3信号的时城展缩 】.1.5倍号的时域运算 (1)相加:n个信号t),J(t),)相加构成一新的信号y(t),即 y(e)-f)+f()+.十n()(m=1,2.) 相加运算用加法器实现,如图1.4所示 (2)相乘:个信号厂(t),∫(t),f()相乘构成一新的信号y(t),即 y(t)=厂)X)X.X∫() 相乘运算用乘法器实现,如图1,5所示,相乘也称调制,乘法器也称调制器。 (3)幅度变化:将信号)乘以实常数a,即得v()=u:),用数乘器实现,如图16所 示数乘器也称比例器或标量乘法器。 e、 a):②w f)、 ☒-w f)a☐) fo 图1.4加法器 图1.5乘法器 图小.6数乘器 (4)微分:将信号f)求一阶导数即得微分信号)0)=.信号的徽分运算用微分器 实现,如图1.7所示. (5)积分:将信号f)在区间(-∞,t)内积分即得积分信号y(:)=f(x)d.信号的积 分运算用积分器实现,如图1,8所示。 @舌☐0□一w旋丹-w=w的 图1.7微分器 图1.8积分器 图1,9系统的定义 -5

1.1.6系统的定义与分类 能够完成某种运算功能的集合体称为系统,如图1.9所示,其中符号H[]称为算子,表 示将输入信号∫()进行某种运算后即得输出信号y(:)。 根据不同的分类原则,系统可分为 (1)动态系统与非动态系统:若系统在t。时刻的响应y(),不仅与。时刻的激励f()有 关,且与区间(一∞,。)的激励有关,则这种系统称为动态系统,也称记忆系统,若系统在时 刻的响应y(t)只与时刻的激励f()有关,而与区间(一∞,)的澈励无关,则这种系统称 为非动态系统或静态系统,也称非记忆系统或即时系统。 (2)线性系统与非线性系统:能同时满足齐次性与叠加性的系统称为线性系统,满足叠加 性是线性系统的必要条件不能同时满足齐次性与叠加性的系统称为非线性系统 (3)时不变系统与时变系统:能满足时不变性质的系统称为时不变系统,否则为时变 系统 (4)因果系统与非因果系统:能满足因果性质的系统称为因果系统,也称可实现系统,因 果系统的特点是,当1>0时作用于系统的激励,t<0时不会在系统中产生响应。不能满足因 果性质的系统称为非因果系统, (5)连续时间系统与离散时间系统 (6)集中参数系统与分布参数系统 1,1.7线性时不变因果系统的性质 设激励ft),(),(t)产生的响应分别为y(t),),y(),并设A,A1,A为任意常 数,则线性时不变因果系统有如下性质: (1)齐次性:AJ)→Ay(): (2)叠加性:()+f2()→为()+(2): (3)线性:A(c)+A,:)→Ay)+A(): (4)时不变性(定常性、延迟性):f(t一t)→y(t一x: (5)微分性:f→dy2, (6)积分性:「fx)dr→了y(rdr: ()因果性:若当t<0时激励f()=0,则当t<0时响应y(t)=0,或者说当t>0时 作用于系统的激励f(:),t<0时不会在系统中产生响应。 1.1.8研究系统的方法 (1)输入输出法与状态变量法。 (2)时域法(经典法、卷积法)与变换域法(FT,LT,ZT法) 1.2例题精选 例1.1写出图1.10所示各信号的时域表达式。 -6