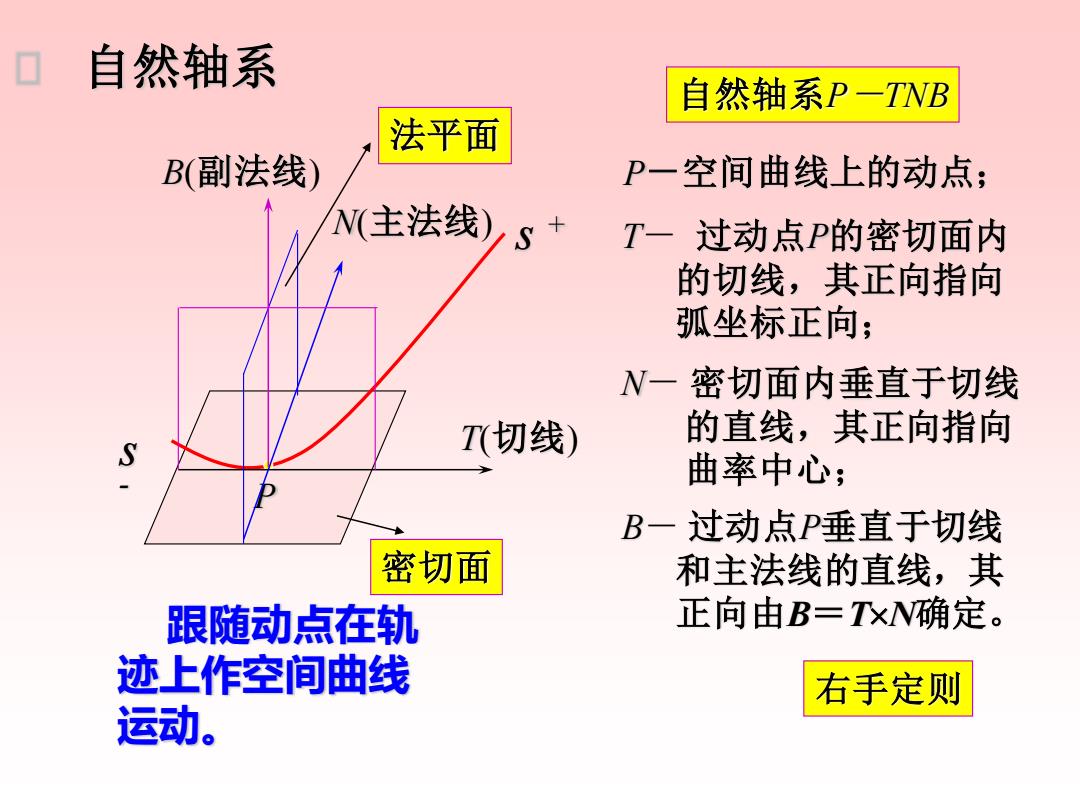
自然轴系 自然轴系P一TNB 法平面 B(副法线) P一空间曲线上的动点; N主法线)S+ T一 过动点P的密切面内 的切线,其正向指向 弧坐标正向; N一密切面内垂直于切线 S T(切线) 的直线,其正向指向 曲率中心; B一过动点P垂直于切线 密切面 和主法线的直线,其 跟随动点在轨 正向由B=TxN确定。 迹上作空间曲线 右手定则 运动
s - s + P T(切线) N(主法线) 自然轴系 B(副法线) 自然轴系P-TNB P-空间曲线上的动点; T- 过动点P的密切面内 的切线,其正向指向 弧坐标正向; N- 密切面内垂直于切线 的直线,其正向指向 曲率中心; B- 过动点P垂直于切线 和主法线的直线,其 跟随动点在轨 正向由B=TN确定。 迹上作空间曲线 运动。 密切面 法平面 右手定则
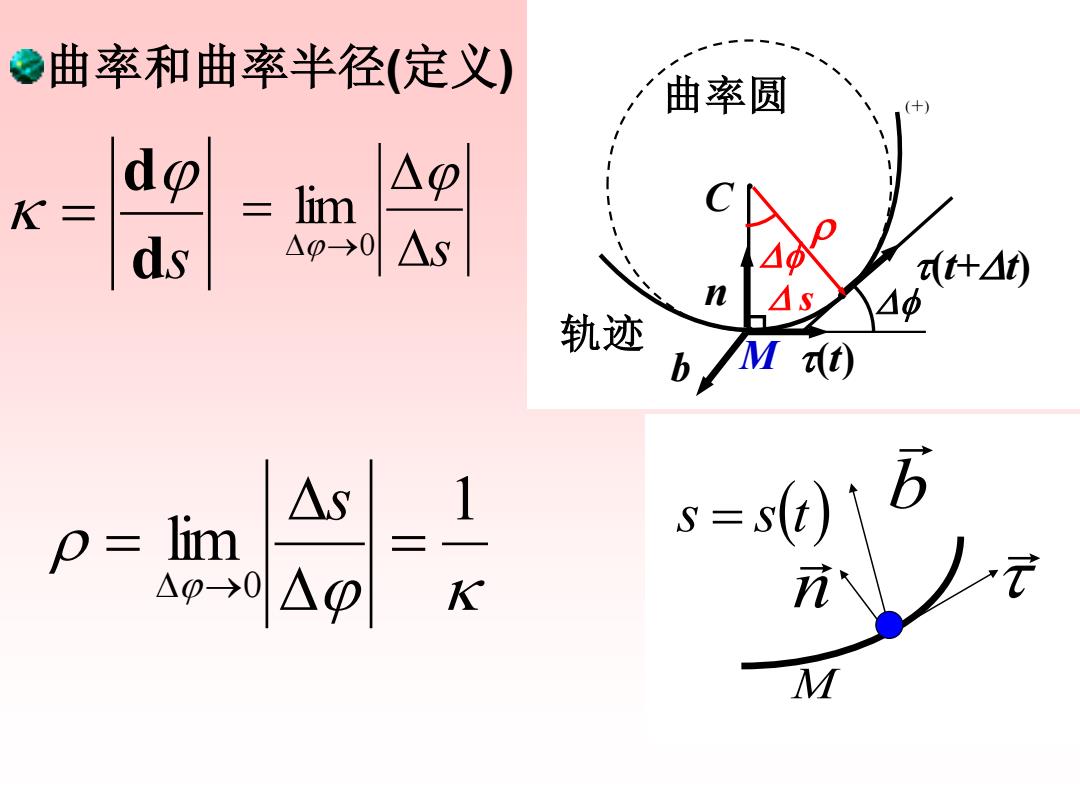
●曲率和曲率半径(定义) 曲率圆 do K 二 lim △型 C ds △00 △s (什△) 轨迹 b M() △S 1 p= lim s=s(t) 二 90△0 K M
(t+Dt) M (t) 轨迹 曲率圆 Df (+) n b C Df D s 1 lim 0 = D D = D → s 曲率和曲率半径(定义) ds d = Ds D = D → 0 lim M n b s = s(t)