2、截断分布 a为随机变量ξ分布范围内的 f() 一个常数 f(5>a)= P(5>a) f(5>c)= f(5) 1/(b-a) P(5>c) b-c -d5 如果ξ服从均匀分布U(a,b),但是它只能在(c, b)内取得样本观测值,那么取得每一个样本 观测值的概率
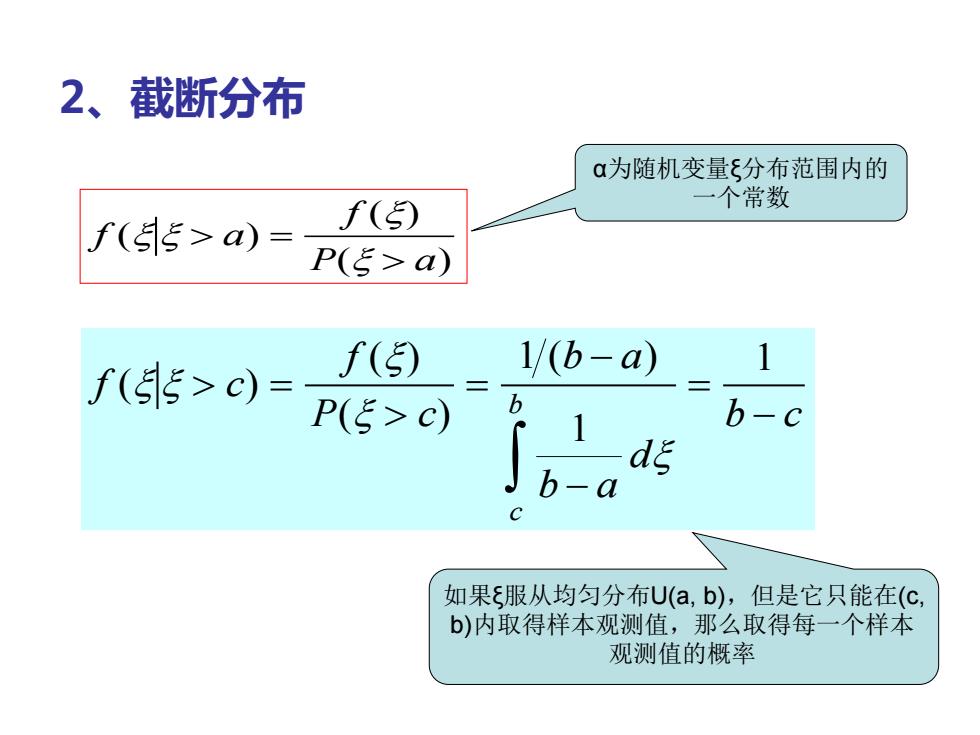
2、截断分布 f a f P a ( ) ( ) ( ) = f c f P c b a b a d b c c b ( ) ( ) ( ) ( ) = = − − = − 1 1 1 如果ξ服从均匀分布U(a, b),但是它只能在(c, b)内取得样本观测值,那么取得每一个样本 观测值的概率 α为随机变量ξ分布范围内的 一个常数
f(5>a)= f(5) P(5>a) (2πo2)-V2e-(5-w)212a2) ξ服从正态 分布 1-Φ(0) 1-Φ(0C) Φ是标准 正态分 P(5>a))=1-(a=1-0 布条件 概率函 数
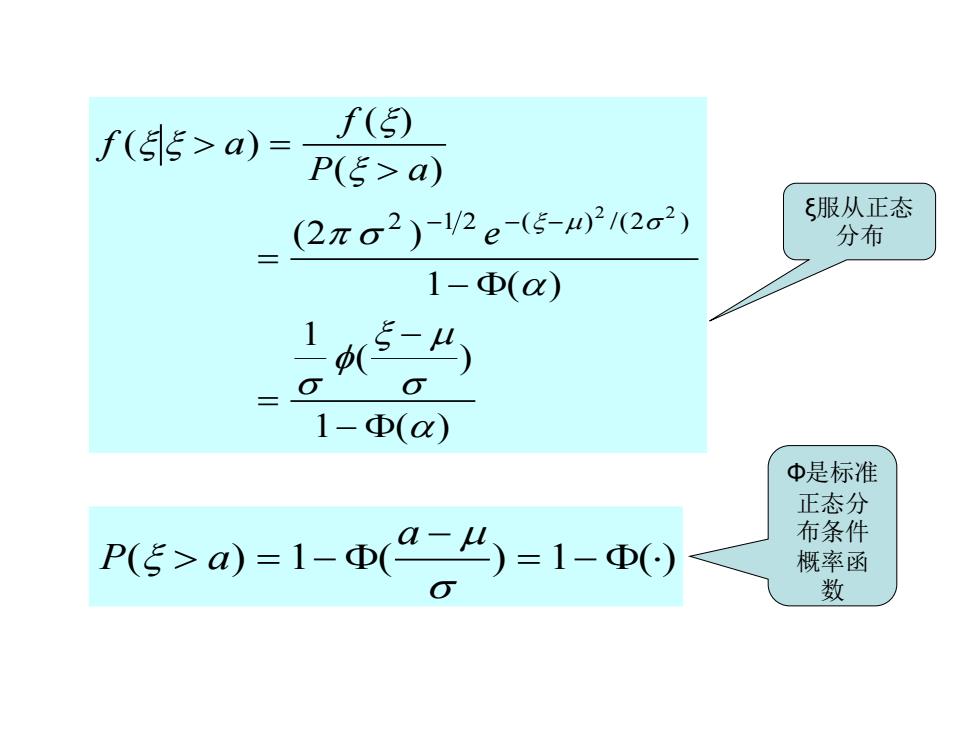
f a f P a e ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) /( ) = = − = − − − − − 2 1 1 1 2 1 2 2 2 2 P a a ( ) ( ) ( ) = − − 1 = 1− ξ服从正态 分布 Φ是标准 正态分 布条件 概率函 数