
静电场边值问题的 唯一性定理 典型的静电问题 给定导体系中各导体的电量或电势以及各导体 的形状、相对位置(统称边界条件),求空间 电场分布,即在一定边界条件下求解。该类问 题称为称为静电场的边值问题
静电场边值问题的 唯一性定理 典型的静电问题 给定导体系中各导体的电量或电势以及各导体 的形状、相对位置(统称边界条件),求空间 电场分布,即在一定边界条件下求解。该类问 题称为称为静电场的边值问题

Q+q 唯一性定理 对于静电场,给定一组边界条件, 空间能否 存在不同的恒定电场分布?—回答:否! 边界条件可将空间里电场的分布唯一地确定 下来 该定理对包括静电屏蔽在内的许多静电问题 的正确解释至关重要 ■论证分三步:引理 叠加原理 一证明
唯一性定理 对于静电场,给定一组边界条件,空间能否 存在不同的恒定电场分布?——回答:否! 边界条件可将空间里电场的分布唯一地确定 下来 该定理对包括静电屏蔽在内的许多静电问题 的正确解释至关重要 论证分三步:引理——叠加原理——证明

极大 几个引理 极小 引理一:在无电荷的空间里电势不可能 有极大值和极小值 ·证明(反证)若有极大,则 V指向P点,E=-VU背离P点 更。=月E·S>0,但面内无电荷矛盾 S 若有极小,同样证明
几个引理 引理一:在无电荷的空间里电势不可能 有极大值和极小值 证明(反证)若有极大,则 极大 极小 若有极小,同样证明
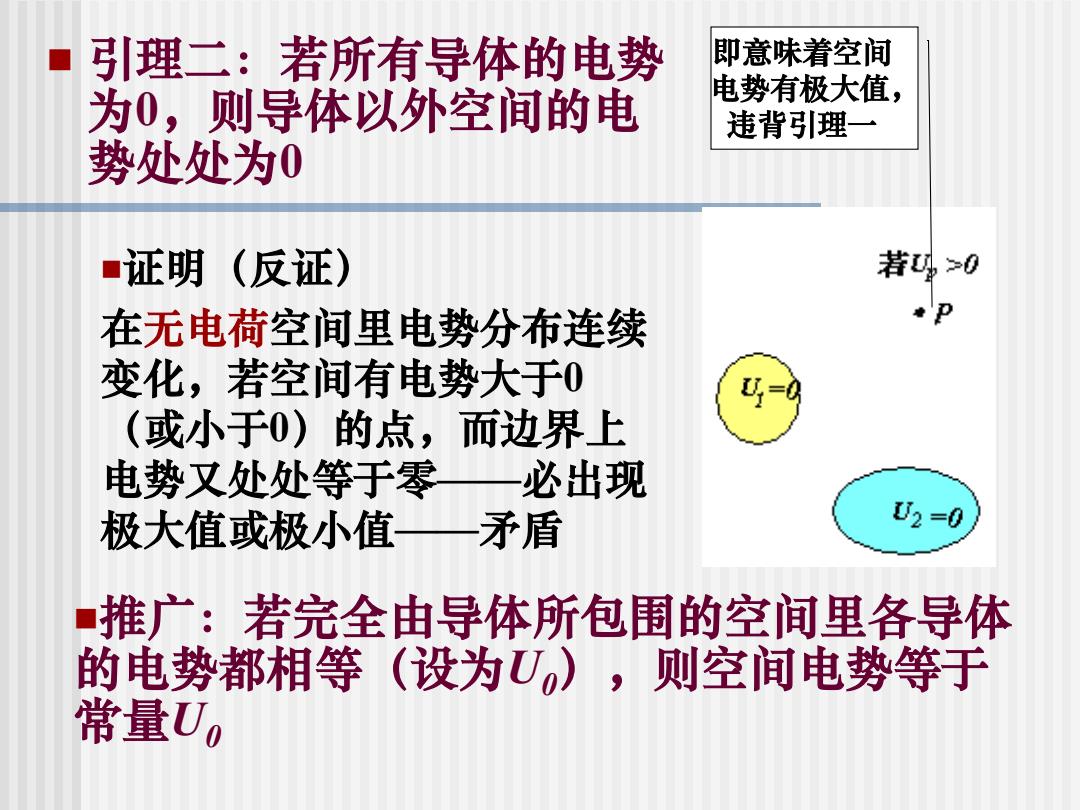
引理二:若所有导体的电势 即意味着空间 为0,则导体以外空间的电 电势有极大值, 违背引理一 势处处为0 ■证明(反证) 若→0 在无电荷空间里电势分布连续 变化,若空间有电势大于0 巧 (或小于0)的点,而边界上 电势又处处等于零 必出现 极大值或极小值— 矛盾 U2=0 推广:若完全由导体所包围的空间里各导体 的电势都相等(设为U),则空间电势等于 常量U0
引理二:若所有导体的电势 为0,则导体以外空间的电 势处处为0 即意味着空间 电势有极大值, 违背引理一 证明(反证) 在无电荷空间里电势分布连续 变化,若空间有电势大于0 (或小于0)的点,而边界上 电势又处处等于零——必出现 极大值或极小值——矛盾 推广:若完全由导体所包围的空间里各导体 的电势都相等(设为U0),则空间电势等于 常量U0
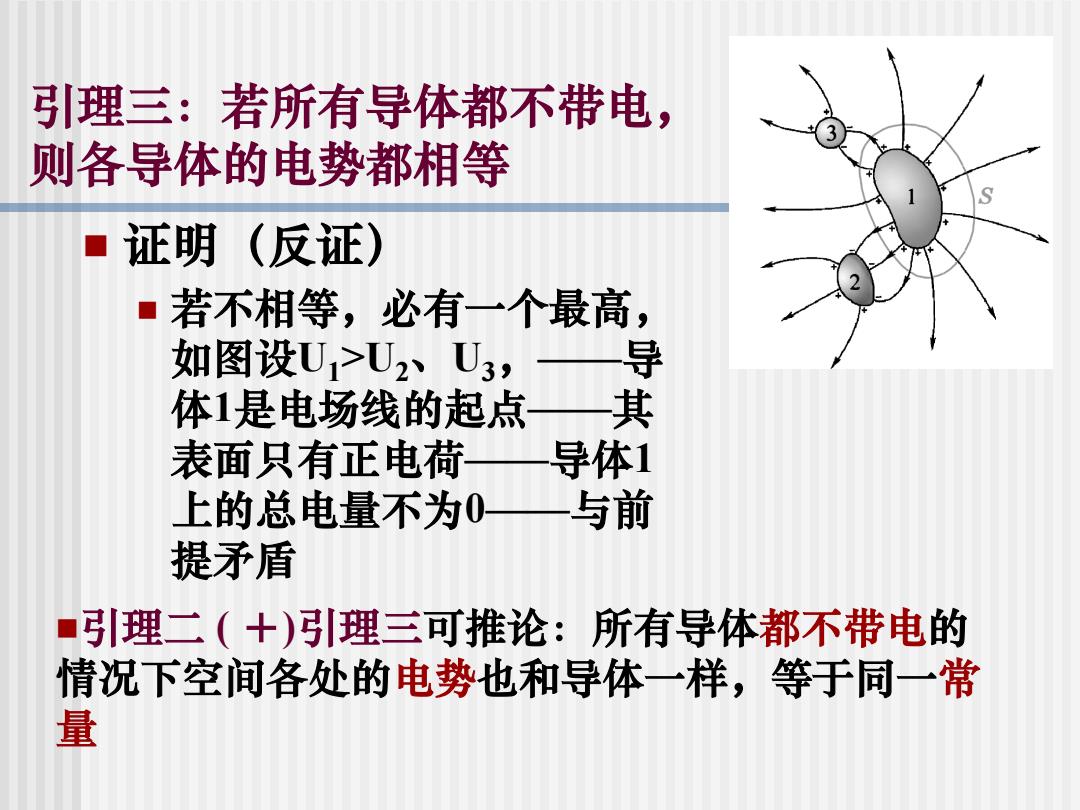
引理三:若所有导体都不带电, 则各导体的电势都相等 证明(反证) 若不相等,必有一个最高, 如图设U1>U2、U3, 体1是电场线的起点—其 表面只有正电荷 导体1 上的总电量不为0 与前 提矛盾 ■引理二(+)引理三可推论:所有导体都不带电的 情况下空间各处的电势也和导体一样,等于同一常 量
引理三:若所有导体都不带电, 则各导体的电势都相等 证明(反证) 若不相等,必有一个最高, 如图设U1>U2、U3,——导 体1是电场线的起点——其 表面只有正电荷——导体1 上的总电量不为0——与前 提矛盾 引理二 ( +)引理三可推论:所有导体都不带电的 情况下空间各处的电势也和导体一样,等于同一常 量