《断裂力学》课程教学资源（书籍教材）断裂力学教程电子版（PDF电子书，共四章）

第一章线弹性断裂力学基础 在裂纹尖端附近，当5|→0时，Zm=Km/√2π5，相应的应力和位移分量依(143小(1-42) 式有 Tx=一 Kmsi √2m 2 Kmco 9 Tx= (1-45) 2m 2 w=! 2r 9 sn Yπ 2 Ⅲ型裂纹的应力强度因子为 Km=乙aV2 (1-46) 2a 000000 图1-5有穿透裂纹并受均匀反平面剪切的无限大板 从而对于图1-5的问题，有 Km=Zm(传2a5= t(5+a四2π5=t√ (1-47) 0V5(5+2a) 般情况下在任意平面问题中，裂纹尖端的奇异场是1型和Ⅱ型结果的叠加，而对 于三维裂纹问题，在沿裂纹边界任意点的奇异场是I、Ⅱ型（平面应变）和Ⅱ型问题解 的线性叠加。 1.2.2对Westergaard方法的修正，双轴载荷效应 首先指出Irwin-Westergaard理论局限性的是薛昌明的论文io,他证明了Westergaard 应力函数只有在双轴均拉时才是准确解。以后Eftis((1927)、Rdewit(1977)12又讨论了 关于修正Westergaard方程的问题。所研究的问题集中在用奇异解所描述的裂纹尖端应 力场与准确应力场之间的差异上。上面的结果即属于奇性解。它相当于采用Williams 特征函数展开法求解得到的应力场级数中取首项（奇性项）的结果，对于其他高阶项的 作用，Cotterell(1966)13]指出：如果将裂纹尖端附近的应力场展开成幂级数，则级数的首

第一章 线弹性断裂力学基础 11 在裂纹尖端附近，当   0时，ZIII  KIII 2 ，相应的应力和位移分量依(1-43)、(1-42) 式有                2 sin 2 2 cos 2 2 sin 2 III III III          K r w r K r K yz xz (1-45) III 型裂纹的应力强度因子为   lim 2 III 0 KIII Z   (1-46) - x y 2a 图 1-5 有穿透裂纹并受均匀反平面剪切的无限大板 从而对于图 1-5 的问题，有 a a a K Z                   2 ( 2 ) ( ) lim ( ) 2 lim 0. III 0 III (1-47) 一般情况下在任意平面问题中，裂纹尖端的奇异场是 I 型和 II 型结果的叠加，而对 于三维裂纹问题，在沿裂纹边界任意点的奇异场是 I、II 型（平面应变）和 III 型问题解 的线性叠加。 1.2.2 对 Westergaard 方法的修正，双轴载荷效应 首先指出 Irwin-Westergaard 理论局限性的是薛昌明的论文[10]，他证明了 Westergaard 应力函数只有在双轴均拉时才是准确解。以后 Eftis(1927)[11]、Rdewit(1977)[12]又讨论了 关于修正 Westergaard 方程的问题。所研究的问题集中在用奇异解所描述的裂纹尖端应 力场与准确应力场之间的差异上。上面的结果即属于奇性解。它相当于采用 Williams 特征函数展开法求解得到的应力场级数中取首项（奇性项）的结果，对于其他高阶项的 作用，Cotterell(1966)[13]指出：如果将裂纹尖端附近的应力场展开成幂级数，则级数的首

断裂力学讲义 项，即奇性主项就是应力强度因子，第二项起着控制裂纹开裂方向的作用，第三项起着 控制裂缝传播稳定性的作用，第四项是确定在裂纹延长线上最大剪应力τ随着离裂纹 尖端的距离是增加还是减小的。Eis(1978)4、Liebowit忆等人(1978)对裂纹尖端的应 力、位移场重新进行了分析，并指出，采用应力的奇性项一般将导致定量甚至定性的错 误结论。他们指出，不可忽视双轴载荷效应。周承惆等人(1979)1用闭合形式的解答讨 论了双轴载荷效应。下面是Efis(1978)等人对Westergaard方程的修正。 I型裂纹 ReZ-yIm Z+B y=ReZ+yIm Z:-B To=-yReZi (1-48) 2w k-1 ReZ-ylmZ:+Bx 2 k+1 21=2 ImZ:-yReZ-By 这里已取Efis等人原文中的20'(z)=Z(z)。 Ⅱ型裂纹 o,=2ImZ+yRe Zi o=-yReZi To=ReZu -yIm Zi-B (1-49) 2m=kImZ+yRe Zn-By 2 2m=-k-山ReZ-yImZ1-Bx 2 这里已取Es等人原文中的2p'(z)=-记(z)。与上面奇性解比较可见两者相差的是与 实常数B有关的项，常数B由问题的应力边界条件确定，上述Westergaard方程的修正 结果的推导可参见4。 Liebowitz和Efis等人用Williams的特征函数展开二项近似指出：即使在张开型的 双轴载荷作用下，奇性解与准确解的应力场之间的差异也是十分明显的。周承惆等人用 封闭形式的解答得出了同样的结论。他们指出通常采用的奇性解（首项近似）并不能就 一般的意义上作为一种好的近似，平行于裂纹平面的载荷的影响表现在局部应力、位移 场级数展开式的第二项上，忽略这一项实际上等价于否认其存在，否认它们对断裂的影 响。实际上，计算表明，在双轴载荷作用下，裂纹前缘的应力、位移场、局部最大剪应 力、等剪应力线、起裂角度、弹性应变能密度和应变能率都反映出明显的双轴载荷效应。 计算和实验都表明裂纹尖端附近的等剪应力线（等色线）明显地依赖于双轴载荷系数h, 12

断裂力学讲义 12 项，即奇性主项就是应力强度因子，第二项起着控制裂纹开裂方向的作用，第三项起着 控制裂缝传播稳定性的作用，第四项是确定在裂纹延长线上最大剪应力 max  随着离裂纹 尖端的距离是增加还是减小的。Eftis(1978)[14]、Liebowitz 等人(1978)[15]对裂纹尖端的应 力、位移场重新进行了分析，并指出，采用应力的奇性项一般将导致定量甚至定性的错 误结论。他们指出，不可忽视双轴载荷效应。周承惆等人(1979)[16]用闭合形式的解答讨 论了双轴载荷效应。下面是 Eftis(1978)等人对 Westergaard 方程的修正。 I 型裂纹 Z y Z By k v Z y Z Bx k u y Z Z y Z B Z y Z B xy y x                    I I I I I I I I I Im Re 2 1 2 Re Im 2 1 2 Re Re Im Re Im      (1-48) 这里已取 Eftis 等人原文中的 2 ( ) ( ) I  z  Z z 。 II 型裂纹 Z y Z Bx k v Z y Z By k u Z y Z B y Z Z y Z xy y x                    II II II II II II II II II Re Im 2 ( )1 2 Im Re 2 1 2 Re Im Re 2Im Re      (1-49) 这里已取 Eftis 等人原文中的 2 ( ) ( ) II  z  iZ z 。与上面奇性解比较可见两者相差的是与 实常数 B 有关的项，常数 B 由问题的应力边界条件确定，上述 Westergaard 方程的修正 结果的推导可参见[14]。 Liebowitz 和 Eftis 等人用 Williams 的特征函数展开二项近似指出：即使在张开型的 双轴载荷作用下，奇性解与准确解的应力场之间的差异也是十分明显的。周承惆等人用 封闭形式的解答得出了同样的结论。他们指出通常采用的奇性解（首项近似）并不能就 一般的意义上作为一种好的近似，平行于裂纹平面的载荷的影响表现在局部应力、位移 场级数展开式的第二项上，忽略这一项实际上等价于否认其存在，否认它们对断裂的影 响。实际上，计算表明，在双轴载荷作用下，裂纹前缘的应力、位移场、局部最大剪应 力、等剪应力线、起裂角度、弹性应变能密度和应变能率都反映出明显的双轴载荷效应。 计算和实验都表明裂纹尖端附近的等剪应力线（等色线）明显地依赖于双轴载荷系数 h

第一章线弹性断裂力学基础 首项近似的奇性解的结果只在h=1时是正确的，其他情况下均相差很远。 双轴载荷下，h对裂纹的开裂方向也有很大的影响，按og判据采用首项近似的 奇性解预言，图1-6情况下，不论h为何值起裂角度9。均为0°。采用两项近似，σ，σ随 9的变化依赖于h的情况示于图1-7。可见当h>2时，ogmx所在的角度9不是0°，而 是随着h增大而加大，当h→0,9。→π/2。 ho h 图1-6含中心穿透裂纹的板受双轴载荷作用 6 3 2 2 h=p 图1-7o。/o随9而变依赖于双轴载荷系数h的情形 1 ho ho 图1-8斜中心裂纹受双轴载荷 13

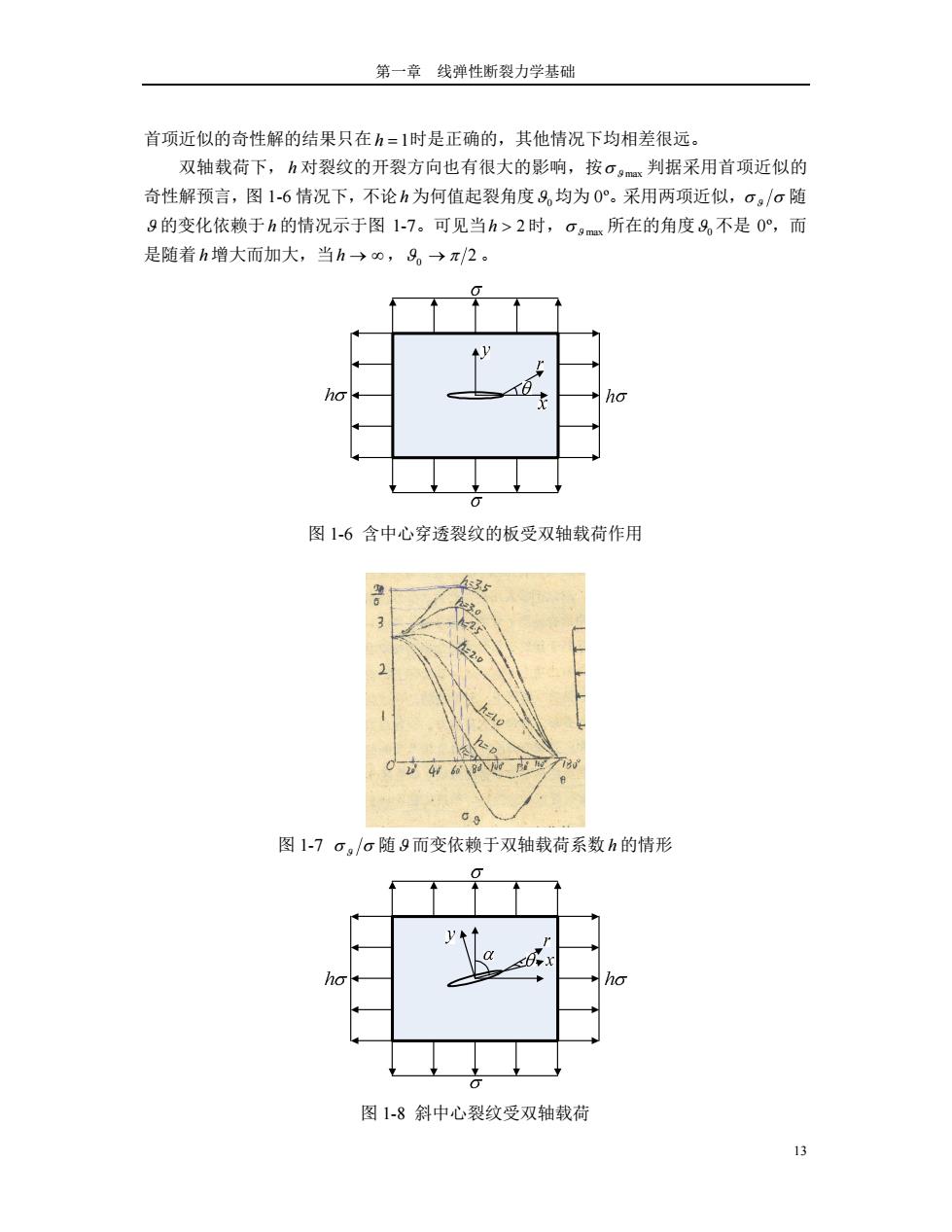
第一章 线弹性断裂力学基础 13 首项近似的奇性解的结果只在 h  1时是正确的，其他情况下均相差很远。 双轴载荷下， h 对裂纹的开裂方向也有很大的影响，按  max 判据采用首项近似的 奇性解预言，图 1-6 情况下，不论h 为何值起裂角度0均为 0º。采用两项近似，   随  的变化依赖于h 的情况示于图 1-7。可见当h  2 时，  max 所在的角度0 不是 0º，而 是随着 h 增大而加大，当h   ，0   2 。 图 1-6 含中心穿透裂纹的板受双轴载荷作用 图 1-7    随 而变依赖于双轴载荷系数 h 的情形 图 1-8 斜中心裂纹受双轴载荷

断裂力学讲义 双轴载荷作用下，斜中心裂纹板的应力强度因子为 2+)-1-h)cos2a] K1=OV (1-50) K(-h)sin 2a 可见只有当h=1时，h才对K1、K无影响。 1.3应力强度因子 前面已指出，K,、K、Km分别称为I、Ⅱ、I型裂纹前缘应力场的强度因子，简 称为应力强度因子。它与坐标，9无关，它不涉及应力和位移在裂纹尖端附近的分布 情况，而是表示应力场强弱程度的物理量。对于线弹性体，应力强度因子与载荷呈线性 关系，并依赖于物体与裂纹的几何形状和尺寸。断裂力学原理的应用很大程度上依赖于 应力强度因子。 确定应力强度因子的方法大体上可分为解析法、数值法和实验法。解析法是其他方 法的基础。由解析法推出的裂纹前缘的应力、位移场的基本方程是许多其他方法的出发 点，在解析法中，广泛使用的是复变函数法（解二维问题）和积分变换法，以及应用弹 性力学守衡律的方法等等。数值法中广泛采用的是有限单元法、边界配置法、边界积分 方程法等。在实验法中有光弹性方法、激光全息和散斑干涉法等。 下面给出几种重要情况下K的计算结果和若干计算K的简便方法。 13.1具有中心穿透裂纹的无限大板 具有中心穿透裂纹的无限大板，在裂纹上、下表面受一对集中力作用，板单位厚度 上，承受的力为P和Q,裂纹右尖端的应力强度因子为 P K1= a+x Vπa Ya-x (1-51) K= Q a+x √aVa-x 2a 图1-9裂纹上下表面有一对集中力 1以

断裂力学讲义 14 双轴载荷作用下，斜中心裂纹板的应力强度因子为                    1( )sin 2 2 [(1 ) 1( ) cos 2 ] 2 II I h a K h h a K (1-50) 可见只有当 h  1时，h 才对 KI 、 KII 无影响。 1.3 应力强度因子 前面已指出， KI 、 KII 、KIII 分别称为 I、II、III 型裂纹前缘应力场的强度因子，简 称为应力强度因子。它与坐标 r ， 无关，它不涉及应力和位移在裂纹尖端附近的分布 情况，而是表示应力场强弱程度的物理量。对于线弹性体，应力强度因子与载荷呈线性 关系，并依赖于物体与裂纹的几何形状和尺寸。断裂力学原理的应用很大程度上依赖于 应力强度因子。 确定应力强度因子的方法大体上可分为解析法、数值法和实验法。解析法是其他方 法的基础。由解析法推出的裂纹前缘的应力、位移场的基本方程是许多其他方法的出发 点，在解析法中，广泛使用的是复变函数法（解二维问题）和积分变换法，以及应用弹 性力学守衡律的方法等等。数值法中广泛采用的是有限单元法、边界配置法、边界积分 方程法等。在实验法中有光弹性方法、激光全息和散斑干涉法等。 下面给出几种重要情况下 K 的计算结果和若干计算 K 的简便方法。 1.3.1 具有中心穿透裂纹的无限大板 具有中心穿透裂纹的无限大板，在裂纹上、下表面受一对集中力作用，板单位厚度 上，承受的力为 P 和Q，裂纹右尖端的应力强度因子为              a x a x a Q K a x a x a P K   II I (1-51) x y P Q x 2a 图 1-9 裂纹上下表面有一对集中力

第一章线弹性断裂力学基础 利用这个结果及叠加原理可解决其他载荷的问题。设沿裂纹面上作用着。，(x,0)和 t(x,0),-a≤x≤a,则 a+xdx a-x (1-52) a+xdx 1.3.2无限大体中有椭圆形片状裂纹 无限大体中有椭圆形片状裂纹，受到垂直于裂纹面的均匀拉伸，椭圆裂纹边缘上任 意位置处的应力强度因子为 图1-10无限大体中的椭圆形片状裂纹 K =Vna nA+gw2 1-53) 40 式中B为该位置的方向与长轴的夹角，。为第二类椭圆积分 b2-a2 63 sin2 9dg (1-54) 在椭圆短轴端点处B=π/2，应力强度因子K,最大 Kimas =Gna/0o (1-55) 对于圆裂纹，即a=b,有。=π/2，则 K1=2o√πa/元 (1-56) 1.3.3半椭圆表面裂纹并受有均匀拉应力 可采用上述深埋裂纹结果并对前后自由表面进行修正得A点处的应力强度因子为 K=M M2 Vna/0o (1-57) 式中 15

第一章 线弹性断裂力学基础 15 利用这个结果及叠加原理可解决其他载荷的问题。设沿裂纹面上作用着 (x )0,  y 和 (x )0, xy  ， a  x  a ，则                  x a x a x a K x a x a x x a K a a xy a a y d 1 ( )0, d 1 II I     (1-52) 1.3.2 无限大体中有椭圆形片状裂纹 无限大体中有椭圆形片状裂纹，受到垂直于裂纹面的均匀拉伸，椭圆裂纹边缘上任 意位置处的应力强度因子为 图 1-10 无限大体中的椭圆形片状裂纹      2 2 2 2 0 I sin cos b a a K   (1-53) 式中  为该位置的方向与长轴的夹角，0为第二类椭圆积分     1 sin d 2 0 2 2 2 2 0     b b a (1-54) 在椭圆短轴端点处    2，应力强度因子 KI 最大 KImax   a 0 (1-55) 对于圆裂纹，即 a  b ，有 2 0   ，则 KI  2 a  (1-56) 1.3.3 半椭圆表面裂纹并受有均匀拉应力 可采用上述深埋裂纹结果并对前后自由表面进行修正得 A 点处的应力强度因子为 KI  M1M 2  a 0 (1-57) 式中