《断裂力学》课程教学资源（书籍教材）断裂力学教程电子版（PDF电子书，共四章）

断裂力学讲义 (1-58) 2w tan a M2= 2w 当a<w时，M2→1，此时短轴端点的最大应力强度因子可依下式计算 K,=1.1o/。 (1-59) 图1-11半椭圆表面裂纹 低应力脆断时，裂纹尖端有小范围屈服，即塑性屈服远小于裂缝特征尺寸，此时， 采用wim的塑性区修正方法，仍可应用线弹性理论结果。在计算应力强度因子时只 要将有效裂纹尺寸代替原真实裂纹尺寸即可（见第二章式(2-9）)。 aet=ao+ry (1-60) 1 平面应力 ,=2 2π0 1 平面应变 4v2π0 式中am为有效裂纹尺寸，a为原有裂纹尺寸，R为塑性区尺寸，r,为修正值，o为屈 服应力。例如，上述半椭圆表面裂纹尖端处于平面应变状态，等效裂纹长度为 1 a K 4W2元 以它代入(1-59)式化简得 K=11 6√a -1.10Va (1-61) V6-0.214(o/o,)2 Jo 式中Q=奶-0.214（σ/o,)2称为裂纹形状因子。 16

断裂力学讲义 16                  w a a w M b a M 2 tan 2 2 1 .0 12 1 2 2 1   (1-58) 当 a  w时， M 2 1，此时短轴端点的最大应力强度因子可依下式计算 KI  1.1  a 0 (1-59) 图 1-11 半椭圆表面裂纹 低应力脆断时，裂纹尖端有小范围屈服，即塑性屈服远小于裂缝特征尺寸，此时， 采用 Irwin[17]的塑性区修正方法，仍可应用线弹性理论结果。在计算应力强度因子时只 要将有效裂纹尺寸代替原真实裂纹尺寸即可（见第二章式(2-9)）。 y a  a  r eff 0 (1-60)                          ， 平面应变 平面应力 2 s I 2 s I 4 2 1 , 2 1 2     K K R ry 式中 eff a 为有效裂纹尺寸， 0 a 为原有裂纹尺寸， R 为塑性区尺寸， y r 为修正值， s 为屈 服应力。例如，上述半椭圆表面裂纹尖端处于平面应变状态，等效裂纹长度为 2 s I 4 2 1            K a 以它代入(1-59)式化简得 Q a a K        1.1 .0 214( ) 1.1 2 s 2 0 I    (1-61) 式中 2 s 2 0 Q    .0 214(  ) 称为裂纹形状因子

第一章线弹性断裂力学基础 C \D Oys 一一B ☑0 R actry 图1-12塑性区修正 1.3.4计算K的几种简便方法 下面介绍工程中实用的几种计算K的简便近似方法。 1.3.4.1双梁、双板模型裂纹问题 当垂直于裂纹平面方向的尺寸较之裂纹尺寸很小时可抽象为双梁或双板模型。张淳 源8曾提出一种既简单又具有较高精确度的方法。这时可依下节方法先求出能量释放 率，然后利用G-K关系求出K。由于K与裂纹尖端A处截面上的内力素（弯矩M,及 剪力Q4)有关，所以便于工程技术人员利用熟悉的内力概念来估算K的大小。具体计 算见下节。 1.3.4.2第一种戴面法 Moroz0v1例曾提出一种近似计算平面问题应力强度因子的方法。想象用一通过裂纹 面的截面将物体切开，列出下部分的平衡方程，并考虑到应力场的渐近解(1-26)，以 Griffith裂纹为例，用平衡方程表示，由于裂纹存在所不能传递的力2ca应与裂纹尖端应 力集中所产生的附加力2o,d相平衡，b依下条件确定 o(b,0)=o,或K√2b=o 即 b=K/2πo2 平衡条件为 2ou-2Po,dr=0 17

第一章 线弹性断裂力学基础 17 图 1-12 塑性区修正 1.3.4 计算 K 的几种简便方法 下面介绍工程中实用的几种计算 K 的简便近似方法。 1.3.4.1 双梁、双板模型裂纹问题 当垂直于裂纹平面方向的尺寸较之裂纹尺寸很小时可抽象为双梁或双板模型。张淳 源[18]曾提出一种既简单又具有较高精确度的方法。这时可依下节方法先求出能量释放 率，然后利用G - K 关系求出 K 。由于 K 与裂纹尖端 A 处截面上的内力素（弯矩 M A 及 剪力 QA）有关，所以便于工程技术人员利用熟悉的内力概念来估算 K 的大小。具体计 算见下节。 1.3.4.2 第一种截面法 Morozov[19]曾提出一种近似计算平面问题应力强度因子的方法。想象用一通过裂纹 面的截面将物体切开，列出下部分的平衡方程，并考虑到应力场的渐近解(1-26)，以 Griffith 裂纹为例，用平衡方程表示，由于裂纹存在所不能传递的力 2a应与裂纹尖端应 力集中所产生的附加力  b r 0 2  d 相平衡，b 依下条件确定   (b )0,   ，或 KI 2b   即 2 2 b  KI 2 平衡条件为 2 2 d 0 0    b a r   

断裂力学讲义 以og=K/W2m代入上式，得 K=GVza 这正是精确解。其他情况下可能得出近似解。 -2ab ■σ 图1-13 1.3.4.3第二种戴面法 Li Xiao-Wei等2o提出另一种截面法近似计算K K=.na 1 6.=(0n+3om) 4 式中on为净应力，口m为平均应力。 1.3.4.4叠加法 由于同型情况（如I型）的应力场方程都相同，K与载荷成线性关系，所以当几种 载荷联合作用时可以用叠加法求应力强度因子。对Ⅱ、Ⅲ型裂纹也是这样。例如对于图 14情况有 Ki =K +Ki -Kie 因Ka=Ke,故 2π0 18

断裂力学讲义 18 以 K r   I 2 代入上式，得 KI   a 这正是精确解。其他情况下可能得出近似解。 2a b 图 1-13 1.3.4.3 第二种截面法 Li Xiao-Wei 等[20]提出另一种截面法近似计算 K K   * a ( 3 ) 4 1  *   n   m 式中 n 为净应力， m 为平均应力。 1.3.4.4 叠加法 由于同型情况（如 I 型）的应力场方程都相同， K 与载荷成线性关系，所以当几种 载荷联合作用时可以用叠加法求应力强度因子。对 II、III 型裂纹也是这样。例如对于图 14 情况有 KIa  KIb  KId  KIe 因 KIa  KIe ，故 a w K K K a     2 2 1 ( ) 2 1 Ia  Ib  Id  

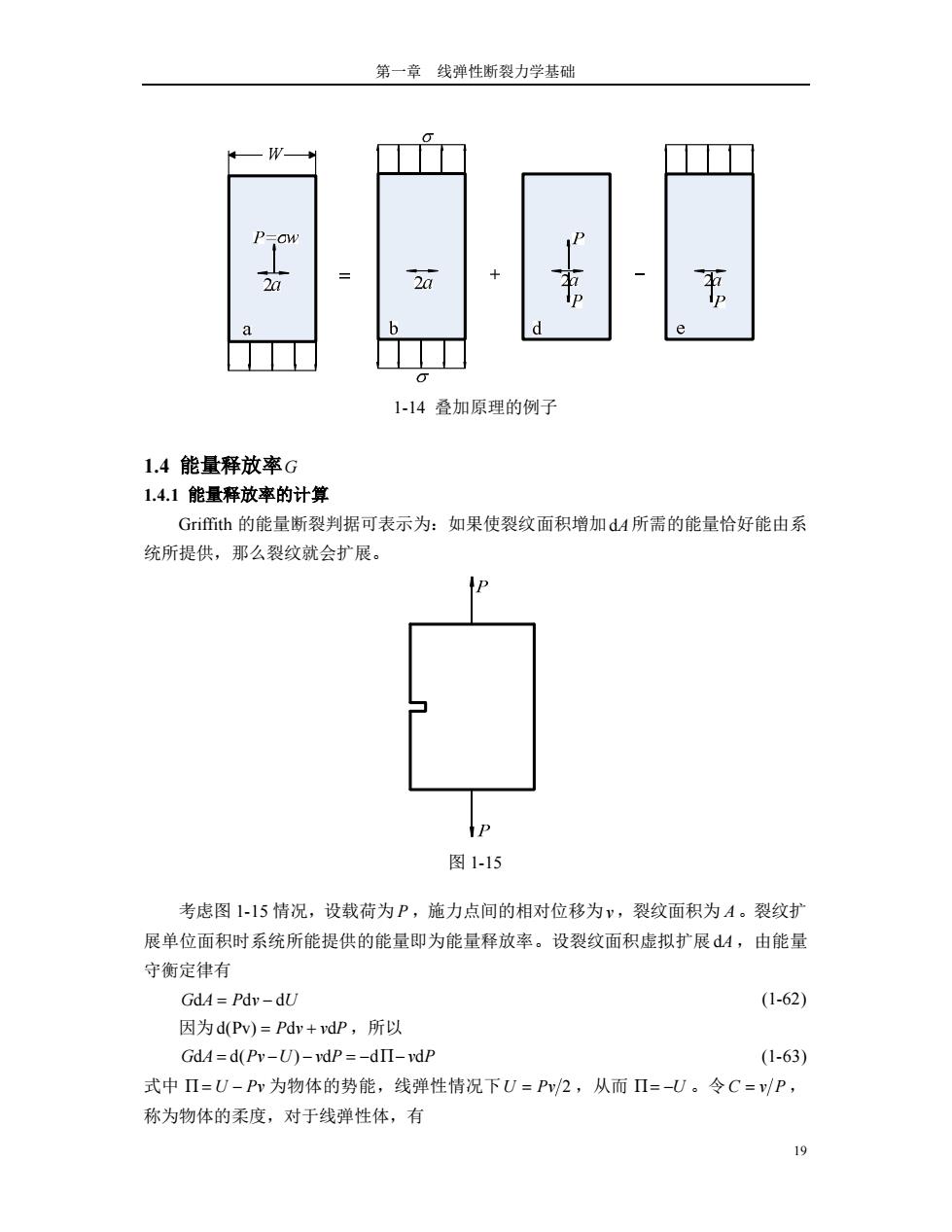
第一章线弹性断裂力学基础 W 等 书 a d 1-14叠加原理的例子 1.4能量释放率G 1.4.1能量释放率的计算 Griffith的能量断裂判据可表示为：如果使裂纹面积增加dA所需的能量恰好能由系 统所提供，那么裂纹就会扩展。 图1-15 考虑图1-15情况，设载荷为P,施力点间的相对位移为v,裂纹面积为A。裂纹扩 展单位面积时系统所能提供的能量即为能量释放率。设裂纹面积虚拟扩展dA,由能量 守衡定律有 GdA=Pdy-dU (1-62) 因为d(Pv)=Pdv+vdP,所以 GdA=d(Py-U)-vdP=-dII-vdP (1-63) 式中Π=U-Pv为物体的势能，线弹性情况下U=P/2,从而Π=-U。令C=v/P, 称为物体的柔度，对于线弹性体，有 19

第一章 线弹性断裂力学基础 19 1-14 叠加原理的例子 1.4 能量释放率G 1.4.1 能量释放率的计算 Griffith 的能量断裂判据可表示为：如果使裂纹面积增加dA所需的能量恰好能由系 统所提供，那么裂纹就会扩展。 图 1-15 考虑图 1-15 情况，设载荷为 P ，施力点间的相对位移为v，裂纹面积为 A。裂纹扩 展单位面积时系统所能提供的能量即为能量释放率。设裂纹面积虚拟扩展dA ，由能量 守衡定律有 GdA  Pdv  dU (1-62) 因为 (d Pv)  Pdv  vdP ，所以 GdA  (d Pv U)  vdP  dΠ vdP (1-63) 式中 Π U  Pv 为物体的势能，线弹性情况下U  Pv 2 ，从而 Π U 。令C  v P ， 称为物体的柔度，对于线弹性体，有

断裂力学讲义 (1-64) (1)固定位移（施力点固定） dv=0,由式(1-62)有 G-- aU (1-65) 对于线弹性体有 G=- v2OC =1 p:0C (1-66) 2C20A-2 8A (2)固定载荷 dP=0,由式(1-63)有 G=- aΠ ) (1-67) 对于线弹性体有 (1-68) (3)载荷和位移都不固定 依式(1-62)、(1-63)有 G=POr_OU_OII OP BA BABAOA (1-69) 对于线弹性体，以U=Pv/2代入上式，得 G=pOv a(1, )=1p:C 2a4 (1-70) 由(1-66)、(1-68)、(1-70)式可见线弹性断裂力学中的能量释放率总可以写成 (1-71) 它不依赖于周围结构或试验机的柔度，而只依赖于裂纹扩展所引起的柔度变化。式(1-71) 称为Irwin-Kies关系，它提供了一个根据试件的柔度，用计算或实验来确定能量释放率 的方法。 能量释放率与应力强度因子K之间有一定的关系。下面我们先证明裂纹沿某扩展方 向的闭合能量释放率E与系统的能量变化率相等。即考虑整个物体的能量平衡与考虑裂 纹尖端的能量平衡是等效的。 考虑单位厚度的穿透裂纹体，受任意载荷的任意形状连续介质裂纹体的能量平衡基 本方程是 20

断裂力学讲义 20 2 2 2 1 2 1 2 1 v C U  Pv  CP  (1-64) (1) 固定位移（施力点固定） dv  0 ，由式(1-62)有 A v U G           (1-65) 对于线弹性体有 A C P A C C v C v A G v                   2 2 2 2 2 1 2 2 (1-66) (2) 固定载荷 dP  0，由式(1-63)有 A P Π G           (1-67) 对于线弹性体有 A C CP P A A U A Π G P P                                2 2 2 1 2 1 (1-68) (3) 载荷和位移都不固定 依式(1-62)、(1-63)有 A P v A Π A U A v G P              (1-69) 对于线弹性体，以U  Pv 2 代入上式，得 A C Pv P A A v G P                2 2 1 2 1 (1-70) 由(1-66)、(1-68)、(1-70)式可见线弹性断裂力学中的能量释放率总可以写成 A C G P    2 2 1 (1-71) 它不依赖于周围结构或试验机的柔度，而只依赖于裂纹扩展所引起的柔度变化。式(1-71) 称为 Irwin-Kies 关系，它提供了一个根据试件的柔度，用计算或实验来确定能量释放率 的方法。 能量释放率与应力强度因子 K 之间有一定的关系。下面我们先证明裂纹沿某扩展方 向的闭合能量释放率 E 与系统的能量变化率相等。即考虑整个物体的能量平衡与考虑裂 纹尖端的能量平衡是等效的。 考虑单位厚度的穿透裂纹体，受任意载荷的任意形状连续介质裂纹体的能量平衡基 本方程是