《断裂力学》课程教学资源（书籍教材）断裂力学教程电子版（PDF电子书，共四章）

断裂力学讲义 1.2.1.11型裂纹 Westergaard选用如下的重为应力函数： 重=ReZ,+ylmZ (1-16) 式中下标1表示I型裂纹。由于(1-16)具有(1-12)的形式，它显然自动满足双调和方程(1-9)， 依(1-10)各应力分量为 o,=ReZ-yImZi ,Re Z+yIm Z (1-17) Tx=-yReZi 对任何解析函数Z()都可得到依上式所确定的应力，问题归结为寻求一个解析函数 Z(:),同时满足考虑问题的边界条件，为了求得位移分量，只须将应(1-17)代入物理 关系及应变位移关系（几何关系）即可。以平面应变状态为例，将(1-17)代入平面应变 状态条件下的物理关系 8,=E0-vo,-v0+v)o,】 (1-18) 6,=E0-2)o,-v1+v)o,】 及几何关系 (1-19) 并积分得 -+[1-2v)ReZ-ylmZ u= E (1-20) v=1+V[2(-v)ImZ,-yReZ E 作为Westergaard方法应用的例子，现讨论带中心穿透裂纹并受均匀双轴拉应力的 无限大板的裂纹尖端应力、位移场。当坐标原点选在裂纹中点时，选取复应力函数 Z(:)-0-a (1-21) 就能满足问题的全部条件 (I)在y=0,-a<x<a处，o,=0,t=0: (2)在z→0,0x=0,=0,tg=0 由于Z(e)除(-a<x<a,y=0)以外是解析函数，又满足问题的边界条件，从而是 问题的解。为了计算裂缝尖端附近的应力、位移场，将坐标原点移至裂纹右尖端处。令 6

断裂力学讲义 6 1.2.1.1 I 型裂纹 Westergaard 选用如下的Φ为应力函数： I I I Φ  ReZ  y ImZ (1-16) 式中下标 I表示 I型裂纹。由于(1-16)具有(1-12)的形式，它显然自动满足双调和方程(1-9)， 依(1-10)各应力分量为               I I I I I Re Re Im Re Im y Z Z y Z Z y Z xy y x    (1-17) 对任何解析函数 ( ) I Z z 都可得到依上式所确定的应力，问题归结为寻求一个解析函数 ( ) I Z z ，同时满足考虑问题的边界条件，为了求得位移分量，只须将应力(1-17)代入物理 关系及应变-位移关系（几何关系）即可。以平面应变状态为例，将(1-17)代入平面应变 状态条件下的物理关系                [(1 ) 1( ) ] 1 [(1 ) 1( ) ] 1 2 2 y y x x x y E E             (1-18) 及几何关系 x u x     ， y v y     ， y u x v xy        (1-19) 并积分得                I I I I 1(2[ )Im Re 1 [(1 2 )Re Im 1 Z y Z E v Z y Z E u     (1-20) 作为 Westergaard 方法应用的例子，现讨论带中心穿透裂纹并受均匀双轴拉应力的 无限大板的裂纹尖端应力、位移场。当坐标原点选在裂纹中点时，选取复应力函数 2 2 I ( ) z a z Z z    (1-21) 就能满足问题的全部条件 (1) 在 y  0， a  x  a 处， y  0， xy  0 ； (2) 在 z   ， x   y   ， xy  0 由于 ( ) I Z z 除（  a  x  a ， y  0）以外是解析函数，又满足问题的边界条件，从而是 问题的解。为了计算裂缝尖端附近的应力、位移场，将坐标原点移至裂纹右尖端处。令

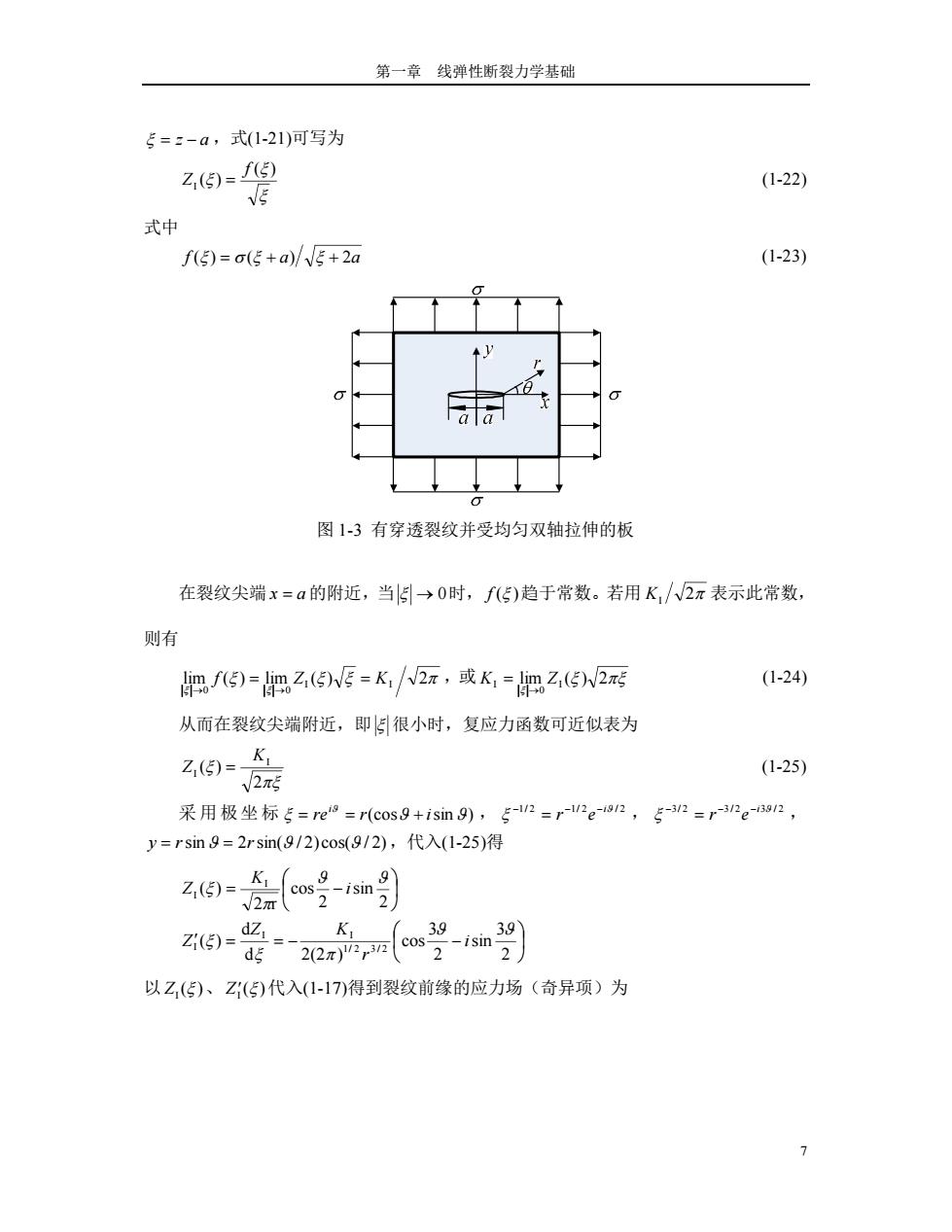
第一章线弹性断裂力学基础 5=z-a,式(1-21)可写为 Z,⑤)=但 (1-22) 式中 f5)=o(5+a)/V5+2a (1-23) aa 图1-3有穿透裂纹并受均匀双轴拉伸的板 在裂纹尖端x=a的附近，当5→0时，f5)趋于常数。若用K,/W2π表示此常数， 则有 f5)=Z店=K/2x,或K,=肥Z(52 (1-24) 从而在裂纹尖端附近，即很小时，复应力函数可近似表为 份高 (1-25) 采用极坐标=e8=r(cos9+isin9),5-2=r-12e-i812，专-312=r3/2e392, y=rsin9=2rsin(9/2)cos(9/2),代入(1-25)得 Z,(5)= 9 v2m 2 2 Z1(5) d☑=- 39 39 2(2π)'232 2 以Z,(5)、Z(5)代入(1-17)得到裂纹前缘的应力场（奇异项）为 >

第一章 线弹性断裂力学基础 7   z  a ，式(1-21)可写为    ( ) ( ) I f Z  (1-22) 式中 f ( )   (  a)   2a (1-23) 图 1-3 有穿透裂纹并受均匀双轴拉伸的板 在裂纹尖端 x  a 的附近，当   0时， f ( )趋于常数。若用 KI 2 表示此常数， 则有       lim ( ) lim ( ) 2 I I 0 0 f  Z  K   ，或    lim ( ) 2 I 0 KI Z   (1-24) 从而在裂纹尖端附近，即  很小时，复应力函数可近似表为   2 ( ) I I K Z  (1-25) 采 用 极 坐 标  (cos sin)  re r i i    ， 2/1 /1 2  2/  i r e     ， 2/3 2/3 3 2/  i r e     ， y  rsin  2rsin( )2/ cos( )2/ ，代入(1-25)得                    2 3 sin 2 3 cos d 2(2 ) d ( ) 2 sin 2 cos 2 r ( ) /1 2 2/3 I I I I I          i r Z K Z i K Z 以 ( ) I Z  、 ( ) I Z  代入(1-17)得到裂纹前缘的应力场（奇异项）为

断裂力学讲义 0x= 1-sinsin 9 39 √2m 2 2 2 K 9 9 39 0y= 1+sin- sin (1-26) V2 2 2 2 K,sin号cos 9 9 39 Tx=- cos 2 对于平面应力问题，有o:=0:对于平面应变问题，有o:=(o.+o,)。式中K称为应 力强度因子，它表示了应力场的强弱程度。K,由(1-24)确定 K=Z,传2店= o(5+a）\2π形=oVa (1-27) -0V5(5+2a 以(1-25)代入式(1-20)并注意到 E=2u(1+v) 得到平面应变情况下裂纹尖端的位移场 u=KL V2 cos1-2v+sin 2 (1-28) -osg 或将平面应力、平面应变两种情况写成统一形式 u=K V2π (1-29) 式中 (3-)/1+v),平面应力 k= (1-30) 3-4 平面应变 值得注意的是基于有穿透裂纹并受均匀双轴拉伸这种特殊情况所得到的上述Ⅰ型裂 纹尖端附近的应力、位移场具有普遍的意义，即对于其他几何情况（如有限尺寸、中心 裂纹、边裂纹)、受力情况（如非均匀受力、集中力）的I型裂纹，裂纹尖端场的表达 式也是相同的，只要裂纹尖端附近的裂纹面上不受面力作用，所不同的只是应力强度因 子，因此，对于特定的结构只要确定K,就可以了。对于Ⅱ、Ⅲ型裂纹尖端也有类似的 结论，各种情况下的应力强度因子可查有关手册8，)。用类似方法可求Ⅱ、Ⅱ型裂纹尖 端场。 8

断裂力学讲义 8                           2 3 cos 2 cos 2 sin 2 2 3 sin 2 1 sin 2 cos 2 2 3 sin 2 1 sin 2 cos 2 I I I                r K r K r K xy y x (1-26) 对于平面应力问题，有  0  z ；对于平面应变问题，有 ( )  z   x  y 。式中 KI 称为应 力强度因子，它表示了应力场的强弱程度。 KI 由(1-24)确定 a a a K Z                   2 ( 2 ) ( ) lim ( ) 2 lim 0 I 0 I (1-27) 以(1-25)代入式(1-20)并注意到 E  2 1(  )          2 sin 2 cos 2 2 2 2 I I I      i r K K Z 得到平面应变情况下裂纹尖端的位移场                          2 2 2 cos 2 sin 2 2 1 2 sin 2 cos 2 I 2 I 2           K r v K r u (1-28) 或将平面应力、平面应变两种情况写成统一形式                          2 ( )1 cos 2 1 2 sin 2 2 ( )1 sin 2 1 2 cos 2 I 2 I 2         k K r v k K r u (1-29) 式中        平面应变 平面应力 3 4 , 3( ) 1( ),    k (1-30) 值得注意的是基于有穿透裂纹并受均匀双轴拉伸这种特殊情况所得到的上述 I 型裂 纹尖端附近的应力、位移场具有普遍的意义，即对于其他几何情况（如有限尺寸、中心 裂纹、边裂纹）、受力情况（如非均匀受力、集中力）的 I 型裂纹，裂纹尖端场的表达 式也是相同的，只要裂纹尖端附近的裂纹面上不受面力作用，所不同的只是应力强度因 子，因此，对于特定的结构只要确定 KI 就可以了。对于 II、III 型裂纹尖端也有类似的 结论，各种情况下的应力强度因子可查有关手册[8,9]。用类似方法可求 II、III 型裂纹尖 端场

第一章线弹性断裂力学基础 1.2.1.1Ⅱ型裂纹 对于Ⅱ型（滑开型）裂纹，可取如下的应力函数 重=-yReZ (1-31) 由(1-10)及(1-18)、(1-19)可求得各应力分量及平面应变情况下位移分量 o,=2ImZn+yRe Zi y=-yReZi Txy ReZu-yIm Zi (1-32) u=+v[2(1-v)imZn+yReZn =栏0-2eZ.-ym21 对于含有长2a穿透裂纹的无限大板，在受纯剪切时，可选用如下形式的解析函数 Zn=ty-a (1-33) 作为复应力函数，则满足全部边界条件。在裂纹尖端附近有Z1=K/√2π5，相应的应 力及位移分量如下 图1-4有穿透裂纹并受均匀平面内剪切的无限大板 39 0x=- Knsin 2+cos-cos √2m 2 2 2 9 9 39 0y= Kusin号cos7co (1-34) √2m 2 2 9 9 39 tw-2m 2 1-sin sin 2 对于平面应力问题，有o.=0;对于平面应变问题，有o.=v(o+o,)。 9

第一章 线弹性断裂力学基础 9 1.2.1.1 II 型裂纹 对于 II 型（滑开型）裂纹，可取如下的应力函数 II ReZII Φ  y (1-31) 由(1-10)及(1-18)、(1-19)可求得各应力分量及平面应变情况下位移分量 [ 1( 2 )Re Im ] 1 1(2[ )Im Re 1 Re Im Re 2Im Re II II II II II II II II II Z y Z E v Z y Z E u Z y Z y Z Z y Z xy y x                          (1-32) 对于含有长 2a穿透裂纹的无限大板，在受纯剪切时，可选用如下形式的解析函数 2 2 II z a z Z    (1-33) 作为复应力函数，则满足全部边界条件。在裂纹尖端附近有 ZII  KII 2 ，相应的应 力及位移分量如下 2a y x 图 1-4 有穿透裂纹并受均匀平面内剪切的无限大板                            2 3 sin 2 1 sin 2 cos 2 2 3 cos 2 cos 2 sin 2 2 3 cos 2 2 cos 2 sin 2 II II II                r K r K r K xy y x (1-34) 对于平面应力问题，有  0  z ；对于平面应变问题，有 ( )  z   x  y

断裂力学讲义 u=Ksm 9 4V2π (1-35) P= Kn r 9 9 V2π cos -(1-2v)+sin2 2 2 或将平面应力、平面应变两种情况写成统一形式 u=K,sing .91 k+1)+cos2 9 4V2π 2L2 2 (1-36) v-- 220-)+sn2 9「1 9 K,为Ⅱ型裂纹的应力强度因子 r5+a0)V2π形=ta Ka(2a) (1-37) 1.2.3.3Ⅱ型裂紋 Ⅲ型裂纹属于反平面应变问题。”=v=0,w≠0，位移垂直于y平面，对于反平 面应变问题，其基本公式为 几何方程：y=- ’y= Ow (1-38) 1 1 物理方程：Ye (1-39) 平衡方程： r=+a=-0 (1-40) ox dy 由(1-38)和(1-40)式得 72w=0 (1-41) w=LImZm (1-42) Y 代入(1-38)、(1-39)式并注意到amZ/ax=mZ,aImZ/ay=ReZ,得 Ts=ImZm (1-43) Tx=ReZm 对于含有长为2a的穿透裂纹的无限大板，在无限远处作用有剪应力t=π时，可 选复应力函数为 Zm=ty-a (1-44) 10

断裂力学讲义 10                           2 1( 2 ) sin 2 cos 2 2 2 2 cos 2 sin 2 II 2 II 2           K r v K r u (1-35) 或将平面应力、平面应变两种情况写成统一形式                          2 1( ) sin 2 1 2 cos 2 2 ( )1 cos 2 1 2 sin 2 II 2 II 2         k K r v k K r u (1-36) KII 为 II 型裂纹的应力强度因子 a a a K Z                   2 ( 2 ) ( ) lim ( ) 2 lim 0. II 0 II (1-37) 1.2.3.3 III 型裂纹 III 型裂纹属于反平面应变问题。u  v  0 ，w  0 ，位移垂直于 xy 平面，对于反平 面应变问题，其基本公式为 几何方程： x w xz     ， y w yz     (1-38) 物理方程： xz xz    1  ， yz yz    1  (1-39) 平衡方程：  0      x y xz yz   (1-40) 由(1-38)和(1-40)式得 0 2  w  (1-41) III Im 1 w Z   (1-42) 代入(1-38)、(1-39)式并注意到 ImZ x  ImZ ， ImZ y  Re Z ，得      III III Re Im Z Z yz xz   (1-43) 对于含有长为 2a的穿透裂纹的无限大板，在无限远处作用有剪应力   yz 时，可 选复应力函数为 2 2 III z a z Z    (1-44)