
离大,配合力也随之分离,待遗传性基本稳定后测定比较可靠。 (3)测定方法不同,其结果不同,精确性不同。 又称同一亲配测法,是指用一个品种或自交系作测验者,其它品种或自交系为被测验者, 测定各被测验者的配合力。早代测定被测验者作父本,晚代测定被测验者作母本,3~4次重 复,随机区组设计(表6-2)。按CA=灭,-4公式计算,并进行方差分析及显著性检验。 表6-2顶交法测定配合力 被测验 者 测验种 H Tester 灭* XX 配合力 (CA)XX *表中试验数据为三次重复的平均值。 (1)该方法的优点:①所配组合数少,便于比较,统计方法简单。②测验者为自交系 或纯系时所测结果近于特殊配合力,测验者为杂合品种或杂交种时,其结果近于普通配合力。 ③适用于雄性不育系或自交不亲和系作测验种,筛选配合力高的自交系来配制一代杂种。 (2)该方法缺点:①试验结果不能分别测算普通配合力和特殊配合力,只能测算混合 的配合力:②所测结果随测验种不同而不同,代表性差,一般只用于亲本的早代粗略测定。 6.2.2.3.2不规则配组法 就是根据亲本选配原则和园艺作物性状遗传规律,重点配制一些比较有希望的组合,作 为分析某些有利用价值的亲本配合力。如表6-1就属于不规则配组法。注意不需要每一个亲 本都参加所有的配组,但每个亲本必须配2个以上的杂交组合(表6-1为完全配组),才能 按6.2和6.3公式计算GCA和SCA。并进行方差分析及显著性检验。此法优点是工作量小, 方法简单,可计算GCA和SCA,该方法己成为优良组合选配中不可缺少的重要环节:缺点 是试验结果可靠性稍差。 6.2.2.3.3轮配法,又称双列杂交(Diallel cross):是指一套系统即做父本又作母本,彼 此进行所有可能的单交,Griffing(1956)根据分析中所包括的材料类型不同,提出四种双 列杂交配组方法(见表6-3)。 表6-3双列杂交轮配方法 I A B C D II A B C D III A B C D IV A B C D A××××AXX××AXX×A ××× B XXXX B XXX B X XX B ×X C××X×C ×XC×× ×C 十 D XXXX D X D XX D N=P2 N=12P(P+1) N=P(P.1) N=I2P(P-1) I.包括正、反交和自交组合,组合总数为N=P2,P为亲本数。 Ⅱ.包括一套正交或反应和自交组合,组合数为:N=12P(P+1) Ⅲ.包括正、反交,但不包括自交组合,组合数为N=P(P-1) 11
11 离大,配合力也随之分离,待遗传性基本稳定后测定比较可靠。 (3)测定方法不同,其结果不同,精确性不同。 又称同一亲配测法,是指用一个品种或自交系作测验者,其它品种或自交系为被测验者, 测定各被测验者的配合力。早代测定被测验者作父本,晚代测定被测验者作母本,3~4 次重 复,随机区组设计(表 6-2)。按 CA = Xi − 公式计算,并进行方差分析及显著性检验。 表 6-2 顶交法测定配合力 测验种 被 测 验 者 A B C D E F G H I J Xi Tester X * × × × × × × × × × × × 配合力 (CA) × × × × × × × × × × × * 表中试验数据为三次重复的平均值。 (1)该方法的优点:①所配组合数少,便于比较,统计方法简单。②测验者为自交系 或纯系时所测结果近于特殊配合力,测验者为杂合品种或杂交种时,其结果近于普通配合力。 ③适用于雄性不育系或自交不亲和系作测验种,筛选配合力高的自交系来配制一代杂种。 (2)该方法缺点:①试验结果不能分别测算普通配合力和特殊配合力,只能测算混合 的配合力;②所测结果随测验种不同而不同,代表性差,一般只用于亲本的早代粗略测定。 6.2.2.3.2 不规则配组法 就是根据亲本选配原则和园艺作物性状遗传规律,重点配制一些比较有希望的组合,作 为分析某些有利用价值的亲本配合力。如表 6-1 就属于不规则配组法。注意不需要每一个亲 本都参加所有的配组,但每个亲本必须配 2 个以上的杂交组合(表 6-1 为完全配组),才能 按 6.2 和 6.3 公式计算 GCA 和 SCA。并进行方差分析及显著性检验。此法优点是工作量小, 方法简单,可计算 GCA 和 SCA,该方法已成为优良组合选配中不可缺少的重要环节;缺点 是试验结果可靠性稍差。 6.2.2.3.3 轮配法,又称双列杂交(Diallel cross):是指一套系统即做父本又作母本,彼 此进行所有可能的单交,Griffing(1956)根据分析中所包括的材料类型不同,提出四种双 列杂交配组方法(见表 6-3)。 表 6-3 双列杂交轮配方法 I A B C D II A B C D III A B C D IV A B C D A × × × × A × × × × A × × × A × × × B × × × × B × × × B × × × B × × C × × × × C × × C × × × C × D × × × × D × D × × D N=P2 N=1/2P(P+1) N=P(P-1) N=1/2P(P-1) I.包括正、反交和自交组合,组合总数为 N=P2,P 为亲本数。 II.包括一套正交或反应和自交组合,组合数为:N=1/2P(P+1) III.包括正、反交,但不包括自交组合,组合数为 N=P(P-1)
6.2.2.3.3.1轮与法的特点 (1)此法不但可以估算普通配合力和特殊配合力,而且还可以深入揭示亲本性状遗传 本质及与环境的关系,前者主要采用固定模式,后者采用随机模式。 (2)各种轮配法所提供的信息量不同,采用的统计公式不同,所获得的遗传信息也是 不同的。如第一种方法工作量大,其中还包括从育种目的来看是不必要的配组,统计程序复 杂,但所获得的遗传信息最多,以便进行深入的遗传分析。 (3)轮配法必须采用数理统计分析的方法,试验一般按完全随机区组设计,重复4~6 次,每小区随机抽取5~20个单株,用单株观测值作基础数据能获得更多的信息,但计算复 杂。对于只是获得配合的分析结果,用小区平均数作基础数据即可。 6.2.2.3.3.1育种上常用的配合分析一半轮配方法。 例题:现有5个番茄品种A、B、C、D、E(P=5),按半轮配法,其组合数=1/25×4=10, 采用完全随机区组设计,重复6次(K=6),按小区计算产量,进行配合力分析。 (1)一般方差分析检验基因型差异 根据原始资料列出区组与组合二间分类表,见表6-4。 总平方和S,=之(x,-) 2 x(14,20,…,21) 区组平方和5S,二,立低-) x17.6,17.3,…,15.9) 组合平方和SS。=k∑(依·j-) x·j13,16,…,23) 误差平方和SSe=SS,-SS,-SSR 方差分析结果见表6-5,方差分析表明,区组间差异不显著,组合间差异极显著,即杂 交组合间存在的真实的差异。则有必要进行配合力分析。前面讲过杂交组合间的方差可以剖 为两部分即普通配合力方差和特殊配合力方差。 表6-4番茄小区产量区组、组合二向分类表 组合x(i=1,2,…,k,Jj=1,2,…,n) 区组 AXB AXC AXD AXE BXC BXD BXE CXD CXE DXE T·jx·j I 14 20 19 10 16 20 11 31 13 20 176 17.6 I 16 16 21 9 12 26 12 27 14 20 173 17.3 IlI 13 14 21 11 11 18 14 29 16 18 175 17.5 IV 9 伊 17 9 9 24 11 25 18 25 165 16.5 V 12 16 21 8 1417 10 24 10 22 154 15.4 VI 14 12 27 7 10 21 8 26 13 21 159 15.9 T·j78 96 126 54 72126 66 162 R 126 990 元.j13 16 219 1221 1127 1421 16.7 12
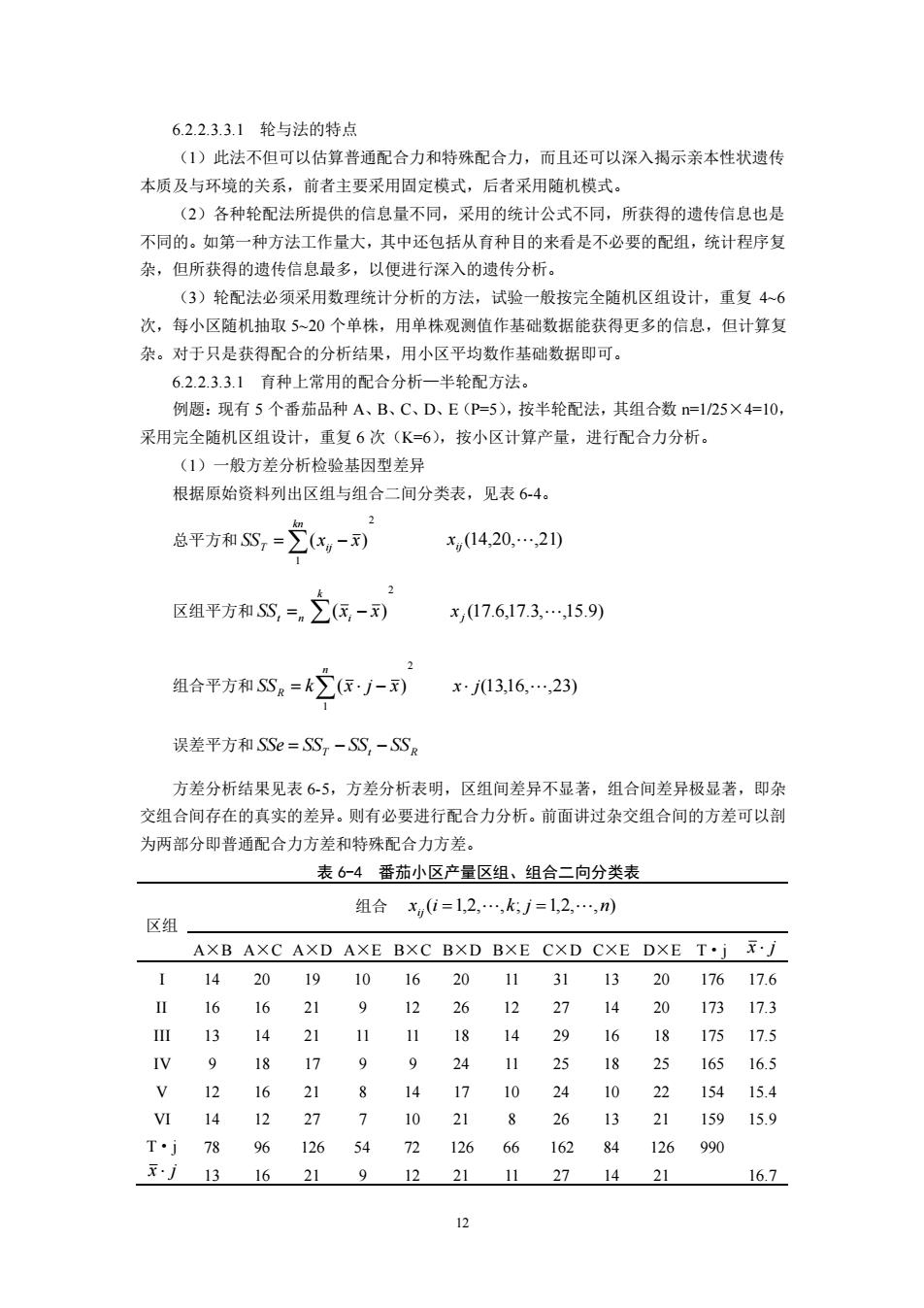
12 6.2.2.3.3.1 轮与法的特点 (1)此法不但可以估算普通配合力和特殊配合力,而且还可以深入揭示亲本性状遗传 本质及与环境的关系,前者主要采用固定模式,后者采用随机模式。 (2)各种轮配法所提供的信息量不同,采用的统计公式不同,所获得的遗传信息也是 不同的。如第一种方法工作量大,其中还包括从育种目的来看是不必要的配组,统计程序复 杂,但所获得的遗传信息最多,以便进行深入的遗传分析。 (3)轮配法必须采用数理统计分析的方法,试验一般按完全随机区组设计,重复 4~6 次,每小区随机抽取 5~20 个单株,用单株观测值作基础数据能获得更多的信息,但计算复 杂。对于只是获得配合的分析结果,用小区平均数作基础数据即可。 6.2.2.3.3.1 育种上常用的配合分析—半轮配方法。 例题:现有 5 个番茄品种 A、B、C、D、E(P=5),按半轮配法,其组合数 n=1/25×4=10, 采用完全随机区组设计,重复 6 次(K=6),按小区计算产量,进行配合力分析。 (1)一般方差分析检验基因型差异 根据原始资料列出区组与组合二间分类表,见表 6-4。 总平方和 2 1 =( − ) kn T ij SS x x (14,20, ,21) ij x 区组平方和 2 = ( − ) k t n i SS x x (17.6,17.3, ,15.9) j x 组合平方和 2 1 = ( − ) n R SS k x j x x j(13,16, ,23) 误差平方和 SSe = SST − SSt − SSR 方差分析结果见表 6-5,方差分析表明,区组间差异不显著,组合间差异极显著,即杂 交组合间存在的真实的差异。则有必要进行配合力分析。前面讲过杂交组合间的方差可以剖 为两部分即普通配合力方差和特殊配合力方差。 表 6-4 番茄小区产量区组、组合二向分类表 区组 组合 x (i 1,2, ,k; j 1,2, ,n) ij = = A×B A×C A×D A×E B×C B×D B×E C×D C×E D×E T·j x j I 14 20 19 10 16 20 11 31 13 20 176 17.6 II 16 16 21 9 12 26 12 27 14 20 173 17.3 III 13 14 21 11 11 18 14 29 16 18 175 17.5 IV 9 18 17 9 9 24 11 25 18 25 165 16.5 V 12 16 21 8 14 17 10 24 10 22 154 15.4 VI 14 12 27 7 10 21 8 26 13 21 159 15.9 T·j 78 96 126 54 72 126 66 162 84 126 990 x j 13 16 21 9 12 21 11 27 14 21 16.7
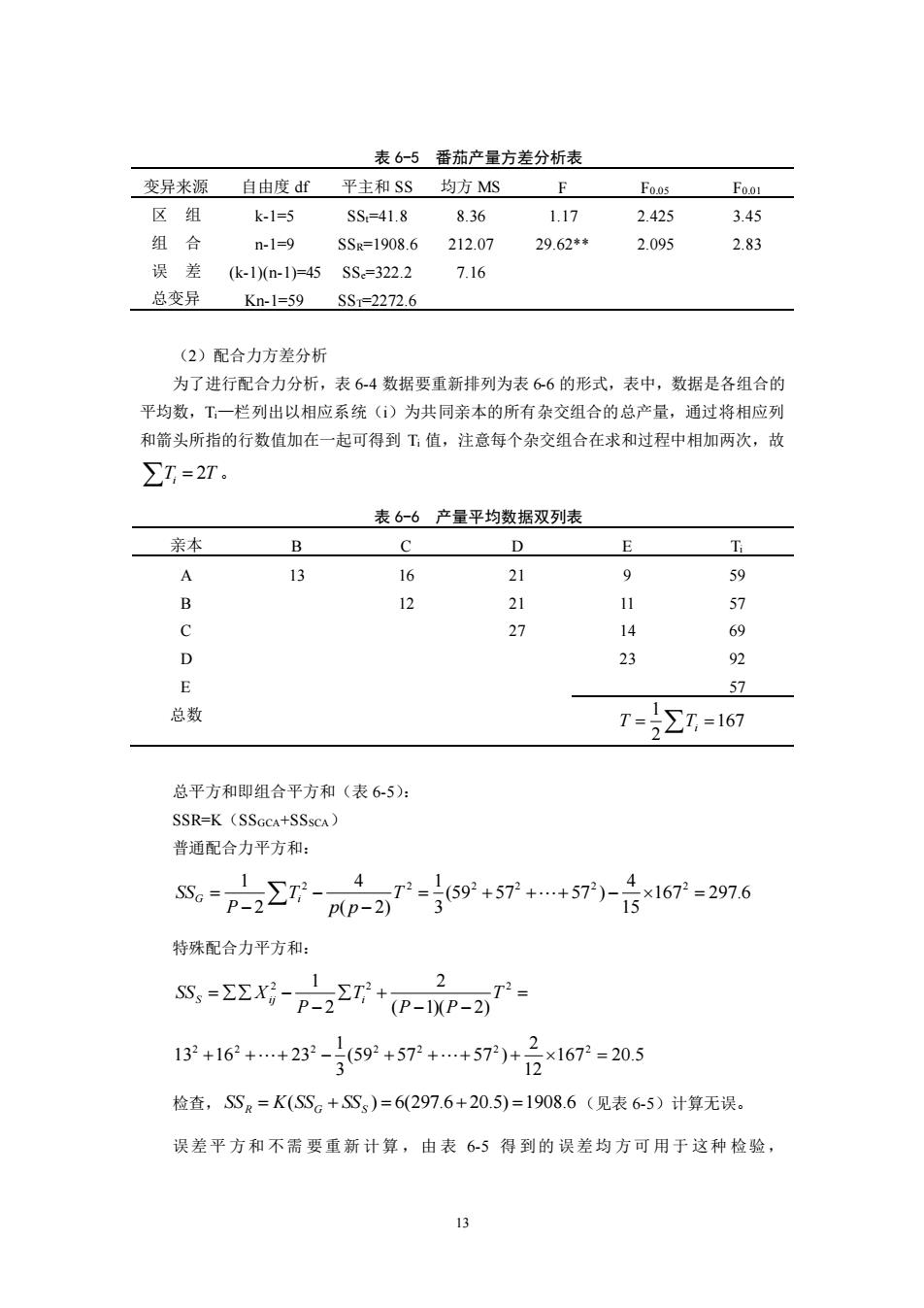
表6-5番茄产量方差分析表 变异来源 自由度df 平主和SS 均方MS F0.05 F0.01 区组 k-1=5 S=41.8 8.36 1.17 2.425 3.45 组合 n-1=9 SSR=1908.6 212.07 29.62* 2.095 2.83 误差 (k-1)n-1)=45 SS=322.2 7.16 总变异 Kn-1=59 SS=2272.6 (2)配合力方差分析 为了进行配合力分析,表64数据要重新排列为表66的形式,表中,数据是各组合的 平均数,T,一栏列出以相应系统()为共同亲本的所有杂交组合的总产量,通过将相应列 和箭头所指的行数值加在一起可得到T:值,注意每个杂交组合在求和过程中相加两次,故 ∑7,=27. 表6-6产量平均数据双列表 亲本 B C D E T A 13 16 21 9 59 B 12 21 11 57 c 27 14 69 D 23 92 E 57 总数 T=3∑7=167 总平方和即组合平方和(表6-5): SSR=K (SSGCA+SSscA) 普通配合力平方和: -2-w47+-16r-96 特殊配合力平方和: T2= (P-1P-2) 13+16+423-69+57++579)+号×167=205 检查,SSR=K(SS。+SS)=6(297.6+20.5)=1908.6(见表6-5)计算无误。 误差平方和不需要重新计算,由表6-5得到的误差均方可用于这种检验, 13
13 表 6-5 番茄产量方差分析表 变异来源 自由度 df 平主和 SS 均方 MS F F0.05 F0.01 区 组 k-1=5 SSt=41.8 8.36 1.17 2.425 3.45 组 合 n-1=9 SSR=1908.6 212.07 29.62** 2.095 2.83 误 差 (k-1)(n-1)=45 SSe=322.2 7.16 总变异 Kn-1=59 SST=2272.6 (2)配合力方差分析 为了进行配合力分析,表 6-4 数据要重新排列为表 6-6 的形式,表中,数据是各组合的 平均数,Ti—栏列出以相应系统(i)为共同亲本的所有杂交组合的总产量,通过将相应列 和箭头所指的行数值加在一起可得到 Ti 值,注意每个杂交组合在求和过程中相加两次,故 Ti = 2T 。 表 6-6 产量平均数据双列表 亲本 B C D E Ti A 13 16 21 9 59 B 12 21 11 57 C 27 14 69 D 23 92 E 57 总数 = =167 2 1 T Ti 总平方和即组合平方和(表 6-5): SSR=K(SSGCA+SSSCA) 普通配合力平方和: = + + + − = − − − = 167 297.6 15 4 (59 57 57 ) 3 1 ( 2) 4 2 1 2 2 2 2 2 2 T p p T P SSG i 特殊配合力平方和: = − − + − = − 2 2 2 ( 1)( 2) 2 2 1 T P P T P SSS Xij i 167 20.5 12 2 (59 57 57 ) 3 1 13 16 23 2 2 2 2 2 2 2 + ++ − + ++ + = 检查, SSR = K(SSG + SSS ) = 6(297.6+ 20.5) =1908.6 (见表 6-5)计算无误。 误差平 方和 不需 要重新 计算 ,由 表 6-5 得 到的 误差均 方可 用于 这种 检验