
例已知两杆电荷线密度为入,长度为L,相距L 求两带电直杆间的电场力。 解 dq Adx dq dq' dq'Adx' o x 2L x 3L Adx Adx' dF 4πE(x'-x) Pdx 4 4π6(x'-x 4π80 3
已知两杆电荷线密度为,长度为L,相距L 解 dq x x dq = dx dq = dx dq 2 0 4 ( ) d d d x x x x F − = − = L L L x x x F x 3 2 0 2 0 2 4 ( ) d d 例 求 两带电直杆间的电场力。 3 4 ln 4 0 2 = O L 2L 3L x

88.2静电场 电场强度卫 一.静电场 ·早期:电磁理论是超距作用理论 ·后来:法拉第提出场的概念 ·电场的特点 (1)对位于其中的带电体有力的作用 (2)带电体在电场中运动,电场力要作功 二.电场强度 场源电荷一产生电场的电荷 带电量足够小 检验电荷 点电荷 在电场中任一位置处: 91 42
§8.2 静电场 电场强度E 一. 静电场 后来: 法拉第提出场的概念 早期:电磁理论是超距作用理论 电场的特点 (1) 对位于其中的带电体有力的作用 (2) 带电体在电场中运动,电场力要作功 二. 电场强度 检验电荷 带电量足够小 点电荷 场源电荷 产生电场的电荷 = = F1 F2 2 q1 q E 在电场中任一位置处:
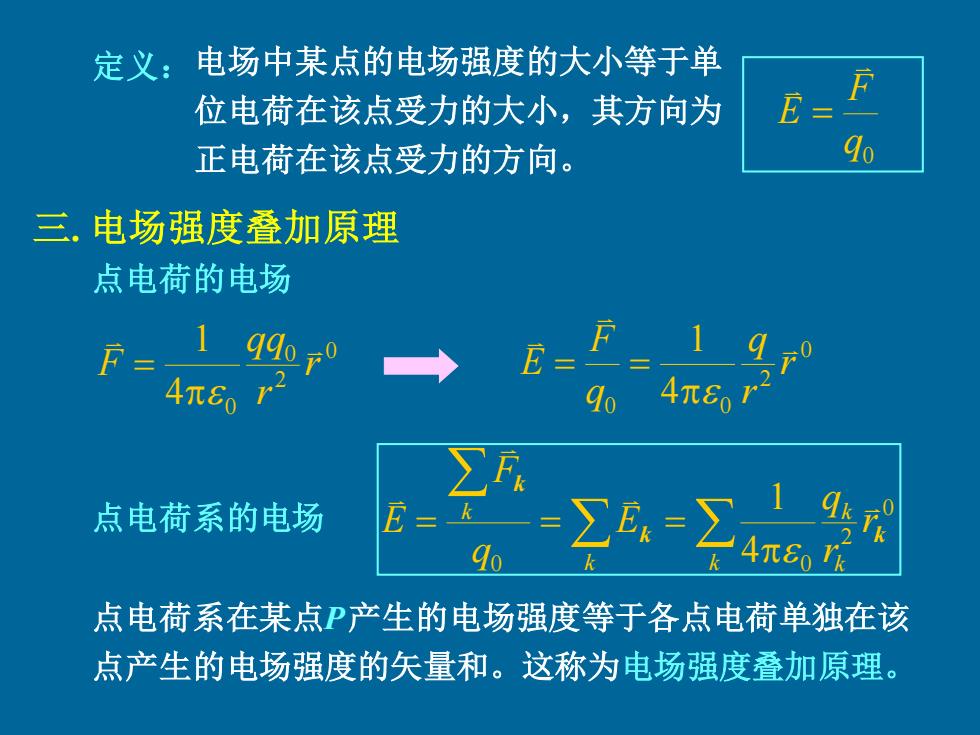
定义:电场中某点的电场强度的大小等于单 位电荷在该点受力的大小,其方向为 E= F 正电荷在该点受力的方向。 9o 三,电场强度叠加原理 点电荷的电场 1 q9o-o E=" 4π607 4πr2 点电荷系的电场 E= ∑E之4r67 点电荷系在某点P产生的电场强度等于各点电荷单独在该 点产生的电场强度的矢量和。这称为电场强度叠加原理
电场中某点的电场强度的大小等于单 位电荷在该点受力的大小,其方向为 正电荷在该点受力的方向。 三. 电场强度叠加原理 点电荷的电场 0 2 0 4 0 1 r r qq F = 0 2 0 0 4 1 r r q q F E = = = = = k k k k k r r q E q F E 0 2 0 4 0 1 k k k 定义: 点电荷系的电场 点电荷系在某点P产生的电场强度等于各点电荷单独在该 点产生的电场强度的矢量和。这称为电场强度叠加原理。 0 q F E =

连续分布带电体 1 dE dE 4πET E= dq Adl (线分布) 入:线密度 odS (面分布) O:面密度 odV (体分布) P:体密度
连续分布带电体 0 2 0 d 4 1 d r r q E = = 0 2 4 0 d r r q E dq = : 线密度 : 面密度 : 体密度 dq r E d P dl (线分布) dS (面分布) dV (体分布)
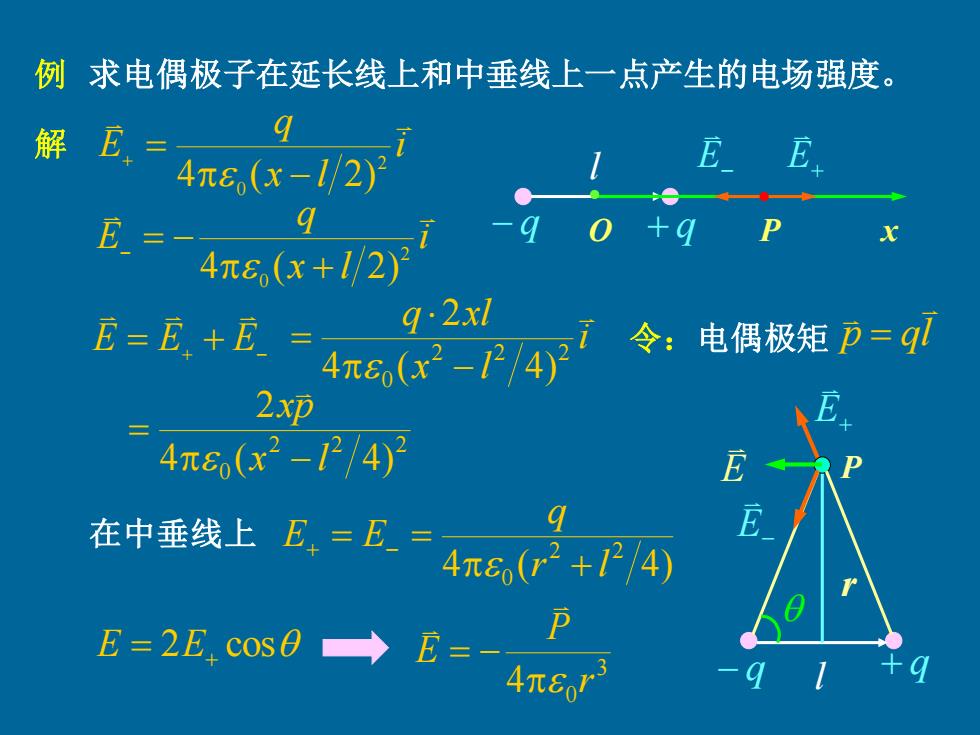
例求电偶极子在延长线上和中垂线上一点产生的电场强度。 解E= q 4π6(x-1/2) E B.=- +q π6,(x+1/2) E=E.+E q:2xl 4πe(cx2-P/4令 电偶极矩p=q 2xp 4元6(x2-1P/4)月 在中垂线上E,=E=4πE(G2+4) E=2Ecos0→ 4π6T
求电偶极子在延长线上和中垂线上一点产生的电场强度。 − q + q l 解 E− E+ i x l q E 2 0 4 ( − 2) + = 例 i O P x x l q E 2 0 4 ( + 2) − = − E = E+ + E− i x l q xl 2 2 2 0 4 ( 4) 2 − = p ql = 2 2 2 0 4 ( 4) 2 x l xp − = 令:电偶极矩 − q + q l P r E− E+ E 4 ( 4) 2 2 0 r l q E E + + = − = 在中垂线上 E = 2E+ cos 3 0 4 r P E = −