
数字角频车 如果定义©=Qr=2x了1了并且将2)的自变量用心表示,周期用u.表示,则 w=2T=2r 即£,)的周期为2。“即为数字角频率,它是模拟域频率对采样频率£的归一化。数字 角频率代表了序列值变化快慢的速率,它只有相对的时间意义,而没有绝对时间和频率的意义。 2)采样定理 如果信号x(t)是实带限信号,且最高频谱不超过2/2,即 Um网m< e2 那么理想采样频谱中,基带频谱以及各次谐波调制频谱彼此是不重迭的,用一个带宽为Ω2的 理想低通滤波器,可以将各次诺波调制频谱滤除,保留不失真的基带频谱,从而不失真地还原 出原来的连续信号。 如果信号最高频谱超过2/2,那么在理想采样 频谱中,各次调制频谱就会互相交叠,出现频谱的 x.(j2) 如 为间明 ,图甲将 (JS (2)为 0 22300 称采样 滤波恢复出来 叠频 XG)+ 像一面镜子,信号频谐超过它时,就会被折迭回来, 造成频谱混淆。 入入入入 奈奎斯特采样定理:要使实信号采样后能够不失 02222.32s 真还原,采样领率必须大于信号最高频率的两倍,即 0.≥20 图1.4、频谱的混叠 实际工作中,为避免频谱混淆,采样频率总是选得 比两倍信 x更 可的 为避免高于折叠频率的杂散须谐 ,采样器前常常加个保护性的前置低通滤波器《抗混叠滤波器,健 0抗混选飞0采样保持器0威字信号@DA变换心 十AD变换器处理器■ 图、抗混叠滤波器 11
11 数字角频率 如果定义 并且将 的自变量用ω表示,周期用ωs表示,则 ωs=ΩsT=2π 即 的周期为 2π。ω即为数字角频率,它是模拟域频率对采样频率 fs的归一化。数字 角频率代表了序列值变化快慢的速率,它只有相对的时间意义,而没有绝对时间和频率的意义。 2)采样定理 如果信号 xa(t)是实带限信号,且最高频谱不超过 s/2,即 那么理想采样频谱中,基带频谱以及各次谐波调制频谱彼此是不重迭的,用一个带宽为 s/2 的 理想低通滤波器,可以将各次谐波调制频谱滤除,保留不失真的基带频谱,从而不失真地还原 出原来的连续信号。 如果信号最高频谱超过 s/2,那么在理想采样 频谱中, 各次调制频谱就会互相交叠,出现频谱的 “混淆”现象,如图。为简明起见,图中将 Xa(j) 作为标量处理,一般 Xa(j)为复数, 交叠也是复数 相加。当出现频谱混淆后,一般就不可能无失真地 滤出基带频谱,用基带滤波恢复出来的信号就要失真。 因此,称采样频率的一半 s/2 为折叠频率,它好 像一面镜子,信号频谱超过它时,就会被折迭 回来, 造成频谱混淆。 奈奎斯特采样定理:要使实信号采样后 能够不失 真还原,采样频率必须大于信号最高频率的两倍 ,即 Ωs≥2Ωmax。 实际工作中,为避免频谱混淆,采样频率总是选得 比两倍信号最高频率 max 更大些,如 s>(3~5)max。 同时,为避免高于折叠频率的杂散频谱 进入采样器造成频谱混淆,采样器前常常加一个保护性的前置低通滤波器(抗混叠滤波器),阻 止高于 S/2 频率分量进入。 抗混叠滤波器

抗混迭滤波器:理想采样信号的频谱是连续信号频谱以采样频率为周期的周期延拓,为避 免采样信号频谱混迭产生失真而处理频带外的高频分量。 3)采样信号的拉氏变换 理想采样后,信号的拉氏变换在S平面上沿虚轴周期延拓,也即R()在S平面上的虚轴 上是周期函数。 4、采样的恢复(恢复信号) 如果理想采样满足奈奎斯特定理,信号最高频率不超过折迭频率,即x心网)- K.Um问<h 0q22 则理想采样的频谱就不会产生混叠,因此有文U)=x.(A),口<Ds 可见,将采样信号£,)通过一个理想低通滤波器(只让基带须谱通过),其带宽等于折 迭频率2s2,频率特性如图1.5。 GG)+ go T i.()-cG) +y-x⑨ 就可滤出原信 r())()-x)2 也就恢复了模拟信号: 图1.5、采样的恢复 u(t=(t) 实际上,理想低通滤波器是不可能实现的,但在满足一定精度的情况下,总可用一个可 实现网络去逼近。 5、采样内插公式 问题:如何由采样信号表示连续信号,采样信号£)通过理想低通滤波器G(2)的响应是什 么 内插公式推导 理想低通G(2)的冲激响应为 g=六工(J)4=天度mn- 2 = 2 频域相乘对应时域卷积,利用卷积公式,则采样信号经理想低通后的输出为 x()-E2()ge-+Hr-x.()5(r-nT)g(-+)dr -三上x8e-04r三x,8e-a) 这里,g-nT称为内插函数,gt-nT)= 血无化-nT) 产e-nT) 其特点为:在采样点T上,函数值为1,其余采样点上为零。 将内蛋面数代入前面的害织公式。可将保样片插公式七构一三5们也三-” E使-) 采样内插公式告诉我们,连续函数x)可以由它的采样值xT来表示,它等于x(T乘 对应的内插函数的总和,即x,)=∑x8- 其中非-m.血- 为内插函数,如图1.6。 行t-) 12
12 抗混迭滤波器:理想采样信号的频谱是连续信号频谱以采样频率为周期的周期延拓,为避 免采样信号频谱混迭产生失真而处理频带外的高频分量。 3)采样信号的拉氏变换 理想采样后,信号的拉氏变换在 S 平面上沿虚轴周期延拓,也即 在 S 平面上的虚轴 上是周期函数。 4、采样的恢复(恢复信号) 如果理想采样满足奈奎斯特定理,信号最高频率不超过折迭频率,即 则理想采样的频谱就不会产生混叠,因此有 ,││< S 可见,将采样信号 通过一个理想低通滤波器(只让基带频谱通过),其带宽等于折 迭频率 S/2,频率特性如图 1.5。 采样信号通过此滤波器后, 就可滤出原信号的频谱: 也就恢复了模拟信号:y(t)=xa(t)。 实际上,理想低通滤波器是不可能实现的,但在满足一定精度的情况下,总可用一个可 实现网络去逼近。 5、采样内插公式 问题:如何由采样信号表示连续信号,采样信号 通过理想低通滤波器 G(j)的响应是什 么? 内插公式推导 理想低通 G(j)的冲激响应为 频域相乘对应时域卷积,利用卷积公式,则采样信号经理想低通后的输出为 这里,g(t-nT)称为内插函数, 其特点为:在采样点 nT 上,函数值为 1,其余采样点上为零。 将内插函数代入前面的卷积公式,可得采样内插公式: 采样内插公式告诉我们,连续函数 xa(t)可以由它的采样值 xa(nT)来表示,它等于 xa(nT)乘上 对应的内插函数的总和,即 其中 为内插函数,如图 1.6
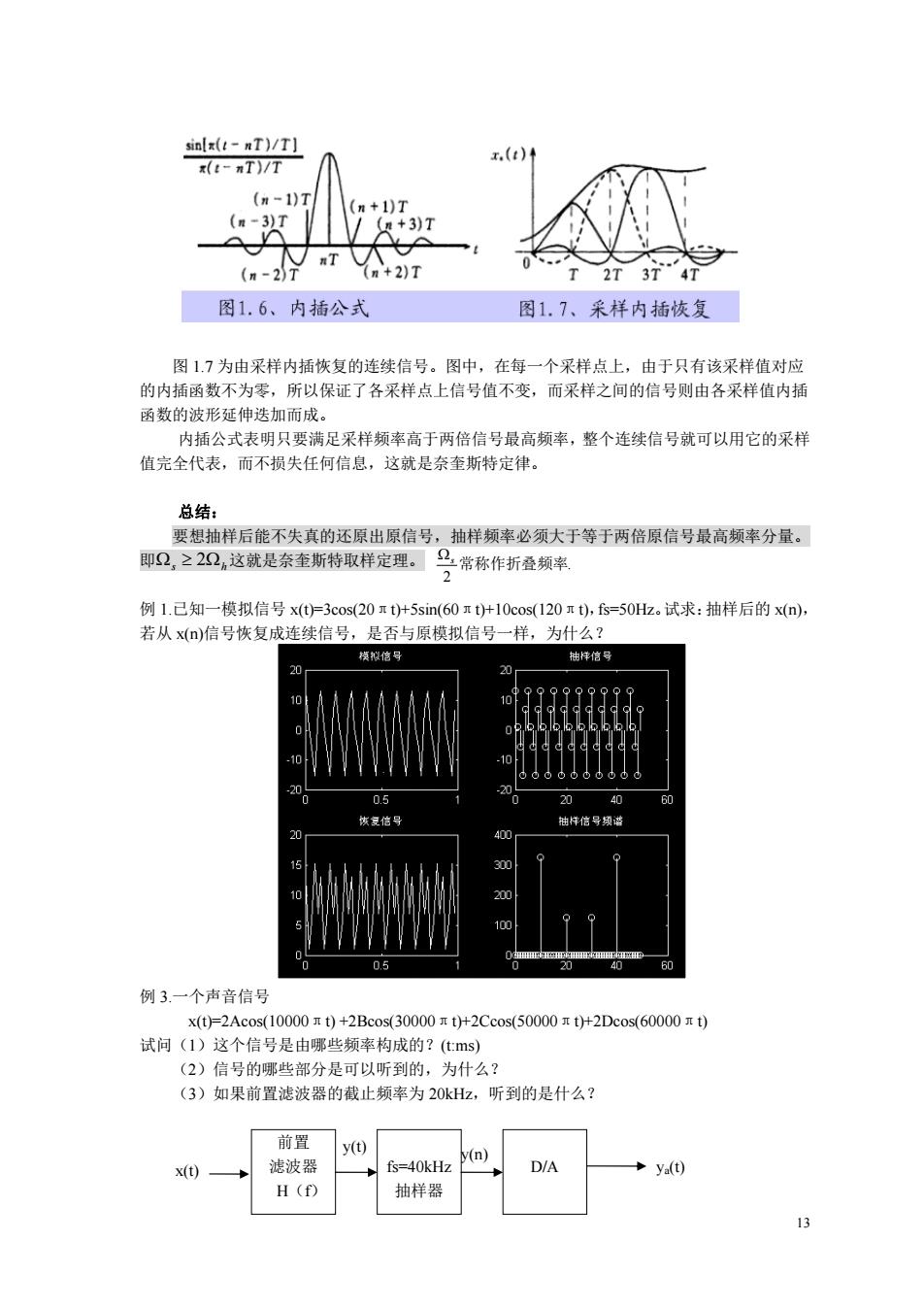
snlx(t-nT)/T】 x(-T)/T (=1)1 +3)T 2T 3 图1.6、内插公式 图1.7、采样内插恢复 图17为由采样内插恢复的连续信号。图中,在每一个采样点上,由于只有该采样值对应 的内插函数不为零,所以保证了各采样点上信号值不变,而采样之间的信号则由各采样值内插 函数的波形延伸迭加而成。 内插公式表明只要满足采样频率高于两倍信号最高频率,整个连续信号就可以用它的采样 值完全代表,而不损失任何信息,这就是奈奎斯特定律。 总结: 要想抽样后能不失真的还原出原信号,抽样频率必须大于等于两倍原信号最高频率分量。 即2,≥22,这就是奈奎斯特取样定理。马常称作折叠领率 例1.已知一模拟信号x3cos(20tH5sim(60H10cos(120),f5=50H。试求:抽样后的xn), 若从x)信号恢复成连续信号,是香与原模拟信号一样,为什么? 模拟信号 袖样德子 10 2 恢复信马 触件信号频达 400 300 0.5 例3.一个声音信号 x(=2Acos(10000)+2Bcos(30000+2Ccos(50000+2Dcos(60000) 试问(1)这个信号是由哪些频率构成的?(cms) (2)信号的哪些部分是可以听到的,为什么? (3)如果前置滤波器的截止频率为20kHz,听到的是什么? 前置 x(t) 滤波器 fs=40kHz y(n) D/A y0 H(f 抽样器 13
13 图 1.7 为由采样内插恢复的连续信号。图中,在每一个采样点上,由于只有该采样值对应 的内插函数不为零,所以保证了各采样点上信号值不变,而采样之间的信号则由各采样值内插 函数的波形延伸迭加而成。 内插公式表明只要满足采样频率高于两倍信号最高频率,整个连续信号就可以用它的采样 值完全代表,而不损失任何信息,这就是奈奎斯特定律。 总结: 要想抽样后能不失真的还原出原信号,抽样频率必须大于等于两倍原信号最高频率分量。 即 这就是奈奎斯特取样定理。 例 1.已知一模拟信号 x(t)=3cos(20πt)+5sin(60πt)+10cos(120πt),fs=50Hz。试求:抽样后的 x(n), 若从 x(n)信号恢复成连续信号,是否与原模拟信号一样,为什么? 例 3.一个声音信号 x(t)=2Acos(10000πt) +2Bcos(30000πt)+2Ccos(50000πt)+2Dcos(60000πt) 试问(1)这个信号是由哪些频率构成的?(t:ms) (2)信号的哪些部分是可以听到的,为什么? (3)如果前置滤波器的截止频率为 20kHz,听到的是什么? s 2h . 2 s 常称作折叠频率 x(t) y(n) ya(t) y(t) fs=40kHz 抽样器 D/A 前置 滤波器 H(f)

第一章习题分类: 。1.1- -1,2,3,4 512 -5,6,7,8 ·§1.39.10 81411 综合题:12 ·提高题:13 ·补充题:14 第二章z变换 ·Z变换 了反变换 ·Z变换性质 Z变换,拉氏变换与DFT傅里叶变换之间的关系 ·系统响应与频率响应 学习要求:熟练掌握付氏变换、Z变换和系统函数。☐ 2-1引言 信号与系统的分析方法有时域、变换域两种 一时域分析法 1连续时间信号与系统:信号的时域运算,时域分解,经典时域分析法,近代时域分析法,卷 积积分。 2离散时间信号与系统:序列的变换与运算,卷积和,差分方程的求解。 变换域分析法 1连续时间信号与系统:信号与系统的频域分析、复频域分析。 2.离散时间信号与系统:Z变换,DFT(FFT)。Z变换可将差分方程转化为代数方程。 2.2Z变换 一、Z变换的定义 利用差分方程可求离散系统的结构及瞬态解。为了分析系统的另外一些重要特性,如稳定 性和频率响应等,需要研究离散时间系统的z变换(类似于模拟系统的拉氏变换),它是分析离 散系统和离散信号的重要工具。 个高散序列x()的Z变换定义为X(2)=立x(a)z· ,其中z为复变量,是 双生受酒产定平面的宝地个中质条:平 单边2变换定义为:X().乏x(a)z·,即只对单边序列(0部分)进行2变换。 单边2变换可以看成是双边变换的一种特例,即因果序列情况下的双边z变换。 二、z变换的收敛域 x回-元 14
14 第一章习题分类: • §1.1——1,2,3,4 • §1.2——5,6,7,8 • §1.3——9,10 • §1.4——11 • 综合题:12 • 提高题:13 • 补充题:14 第二章 z 变换 • Z 变换 • Z 反变换 • Z 变换性质 • Z 变换,拉氏变换与 DFT 傅里叶变换之间的关系 • 系统响应与频率响应 学习要求:熟练掌握付氏变换、Z 变换和系统函数。 2-1 引言 信号与系统的分析方法有时域、变换域两种。 一.时域分析法 1.连续时间信号与系统:信号的时域运算,时域分解,经典时域分析法,近代时域分析法,卷 积积分。 2.离散时间信号与系统:序列的变换与运算,卷积和,差分方程的求解。 二.变换域分析法 1.连续时间信号与系统:信号与系统的频域分析、复频域分析。 2.离散时间信号与系统:Z 变换,DFT(FFT)。Z 变换可将差分方程转化为代数方程。 2.2 Z 变换 一、Z 变换的定义 利用差分方程可求离散系统的结构及瞬态解。为了分析系统的另外一些重要特性,如稳定 性和频率响应等,需要研究离散时间系统的 z 变换(类似于模拟系统的拉氏变换),它是分析离 散系统和离散信号的重要工具。 一个离散序列 x(n)的 Z 变换定义为 ,其中 z 为复变量,是 一个以实部为横坐标,虚部为纵坐标构成的平面上的变量,这个平面也称 z 平面。 双边 z 变换定义为: 单边 z 变换定义为: ,即只对单边序列(n>=0 部分)进行 z 变换。 单边 z 变换可以看成是双边 z 变换的一种特例,即因果序列情况下的双边 z 变换。 二、z 变换的收敛域

一般,序列的?变换 并不一定对任何飞值都收敛,z平面上使上述级数 收敛的区域称为“收敛域”, 一般Z变换的收敛域为:R-(z(R 我们知道,级数一致收敛的条件是绝对值可和,因此z平面的收敛域应满足 (n)z 因为对于实数序列, 元k()z=Σk()"<。 因此 2值在一定范周围内才能满足 对可和条件,这个范围一般表不为 或空心圆 jIm[z] )四种序列的2变换收 R a有限长序列 其它 ,收敛域为0水∞。 1.11,乙变换的收敛城 因为X(2)是有限项的级数和,只要级数每一项有界,有限项和也有界,所以有限长序列z变换 的收敛域取决于z<o,≤n≤a 显然在整个开域(0,∞)都能满足以上条件,因此有限长序列的收敛域是除0及∞两个点 (对应n>0和n<0不收敛)以外的整个Z平面:0水∞。如果对1,加以一定的限制,如 n120或n20 则根据条件z(∞(n≤n≤),收敛域可进一步扩大为包括0点或∞点的半 开域:J0<s∞m≥0 0到8K0n2≤0 例1、序列x()=6(m) X(z)=Σ6(r)z"=1xz0=1 由于1,==0,其收敛域为整个闭域子平面,0≤z≤∞。 例2.矩形序列x(n)=R(n) x()- k(w)1-1++1-1-m+w-w 等比级数求和 ()=101zK0 b.右边序列 指x(n)只在n≥n,有值,而n(m时,X(n)=0,这时x(a)-x)z 其收敛域为收敛半径R以外的z平面,即2>R 右边序列中最重要的 种序列是“因果序列”即10的右边序列,因果序列只在≥0有值, n(0时,x(n)=0,其z变换为:X(z)=2x(a)z z变换的收敛域包括∞点是因果序列的特征】 证明: 如果nl<0,则选择任一整数n2>0,使得 三kz三kz+三ka)z 由于第一项为有限长序列的乙变换,在(0, )收敛。对于第 之K清足,R·<。所以Xa时R上收敛。0,找味R 由此可进一步证明、在R圆以外、即R 15
15 一般,序列的 Z 变换 并不一定对任何 z 值都收敛,z 平面上使上述级数 收敛的区域称为“收敛域”。一般 Z 变换的收敛域为: Rx-〈|z|〈Rx+ 我们知道,级数一致收敛的条件是绝对值可和,因此 z 平面的收敛域应满足 因为对于实数序列, 因此,|z|值在一定范围内才能满足绝对可和条件,这个范围一般表示为 Rx-〈|z|〈Rx+ 。 这就是收敛域,一个以 Rx-和 Rx+为半径的两个圆所围成的环形区域,Rx- 和 Rx+ 称为收敛半径, Rx-和 Rx+的大小,即收敛域的位置与具体序列有关,特殊情况为 Rx-或 Rx+等于 0,这时圆环变成圆 或空心圆。 四种序列的 Z 变换收敛域 a. 有限长序列 序列 ,其 Z 变换 ,收敛域为 0<|z|<∞。 因为 X(z)是有限项的级数和,只要级数每一项有界,有限项和也有界,所以有限长序列 z 变换 的收敛域取决于|z|-n<∞, ≤n≤ 。 显然|z|在整个开域(0,∞)都能满足以上条件,因此有限长序列的收敛域是除 0 及∞两个点 (对应 n>0 和 n<0 不收敛)以外的整个 Z 平面:0<|z|<∞。如果对 n1,n2 加以一定的限制,如 n1≥0 或 n2≤0,则根据条件|z|-n<∞(n1≤n≤n2),收敛域可进一步扩大为包括 0 点或∞点的半 开域: 例 1、序列 x(n)=δ(n) 由于 ,其收敛域为整个闭域子平面,0≤|Z|≤∞。 例 2. 矩形序列 x(n)=RN(n) 等比级数求和 b. 右边序列 指 x(n)只在 n≥n1,有值,而 n〈n1时,x (n)=0,这时 其收敛域为收敛半径 Rx-以外的 z 平面,即|z|>Rx-。 右边序列中最重要的一种序列是“因果序列”即 n1=0 的右边序列,因果序列只在 n≥0 有值, n〈0 时,x(n)=0,其 z 变换为: z 变换的收敛域包括∞点是因果序列的特征。 证明: 如果 n1<0,则选择任一整数 n2>0,使得 由于第一项为有限长序列的 Z 变换,在(0,∞)收敛。对于第二项,总能在(0,∞)找到|z|=R (如 R≥2MAX[X(n)])满足 所以 X(z)在|z|=R 上收敛。 由此可进一步证明,在 R 圆以外,即 R<|z|<∞,x(Z)也必收敛。 再看第二项,由于 n>n2≥0,|Z|>R,因此|z|-n<R-n,故