
拉压[例11图示杆的A、B、C、D点分别作用着大小为5P、8P、4PP的力,方向如图,试画出杆的轴力图DBCOPpPBPDCBPDPPBP解:求OA段内力N:设置截面如图ZX=0 N -P +P:- P-P,= 0N -5P+8P-4P-P=0N.=2P
[例1] 图示杆的A、B、C、D点分别作用着大小为5P、8P、4P、 P 的力,方向如图,试画出杆的轴力图。 解: 求OA段内力N1:设置截面如图 A B C D PA PB PC PD O A B C D PA PB PC PD N1 X = 0 N1 − PA + PB − PC − PD = 0 N1 −5P +8P − 4P − P = 0 N1 = 2P
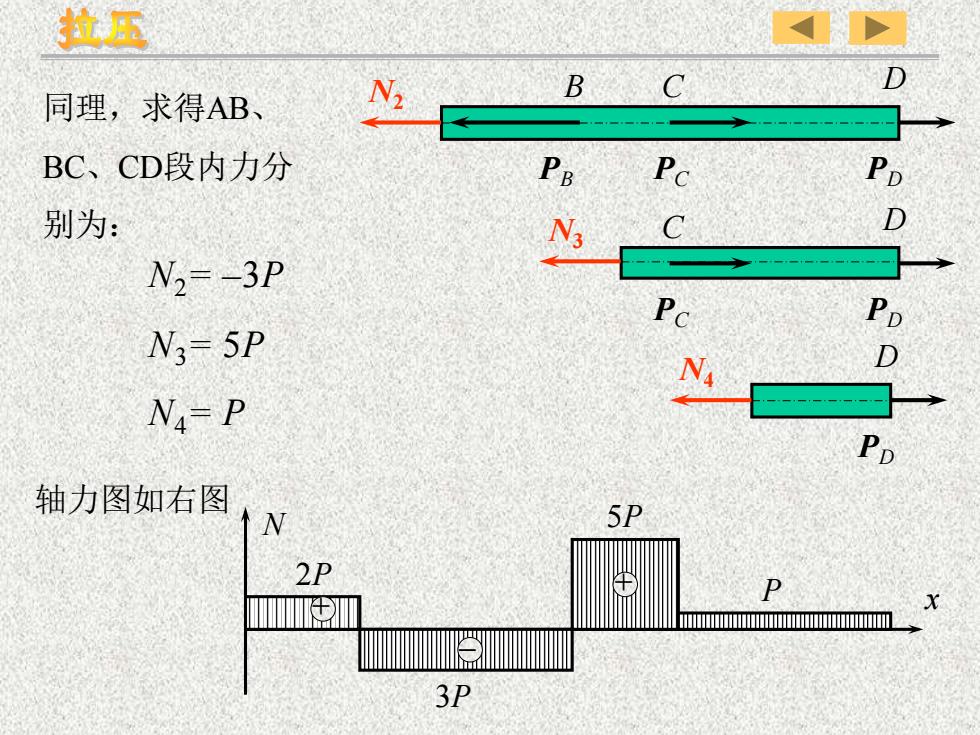
拉压DBCN2同理,求得AB、BC、CD段内力分PcPDPBD别为:CN3N2- -3PPcPDN3= 5PDNN4- PPp轴力图如右图5PN2PPUm3P
同理,求得AB 、 BC 、CD段内力分 别为: N2= – 3 P N3= 5 P N4= P 轴力图如右图 B C D PB P C PD N2 C D P C PD N3 DPD N4 N x 2 P 3 P 5 P+ P + –
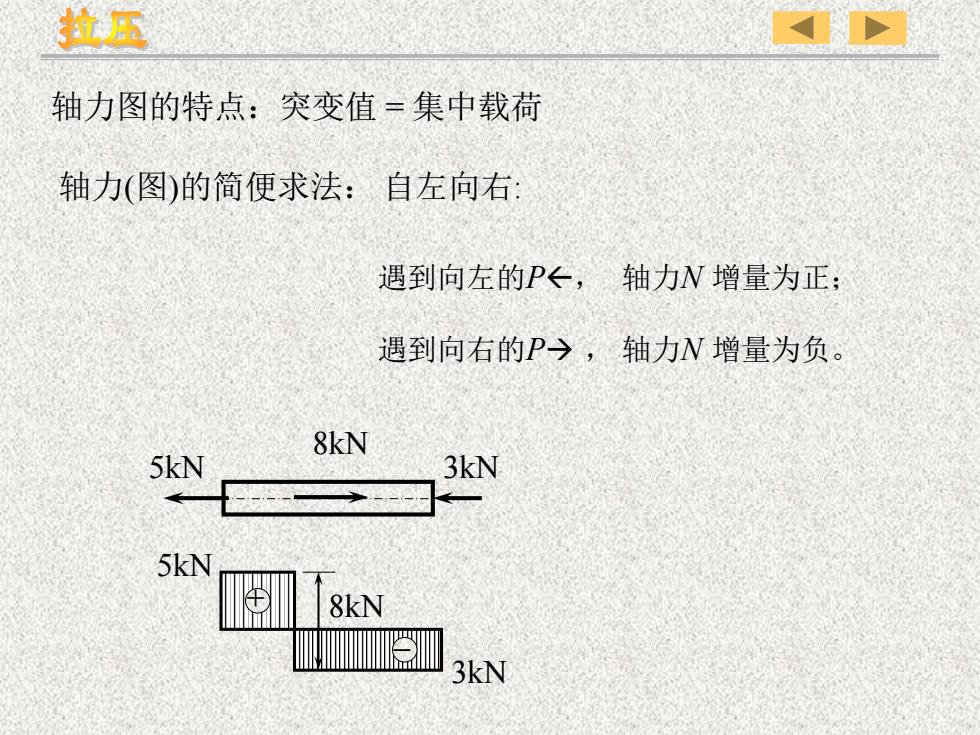
拉压轴力图的特点:突变值=集中载荷轴力(图)的简便求法:自左向右遇到向左的P←,轴力N 增量为正;遇到向右的P,轴力N增量为负。8kN5kN3kN5kN8kNX3kN
轴力(图)的简便求法: 自左向右: 轴力图的特点:突变值 = 集中载荷 遇到向左的P, 轴力N 增量为正; 遇到向右的P→ , 轴力N 增量为负。 5kN 8kN 3kN + – 3kN 5kN 8kN
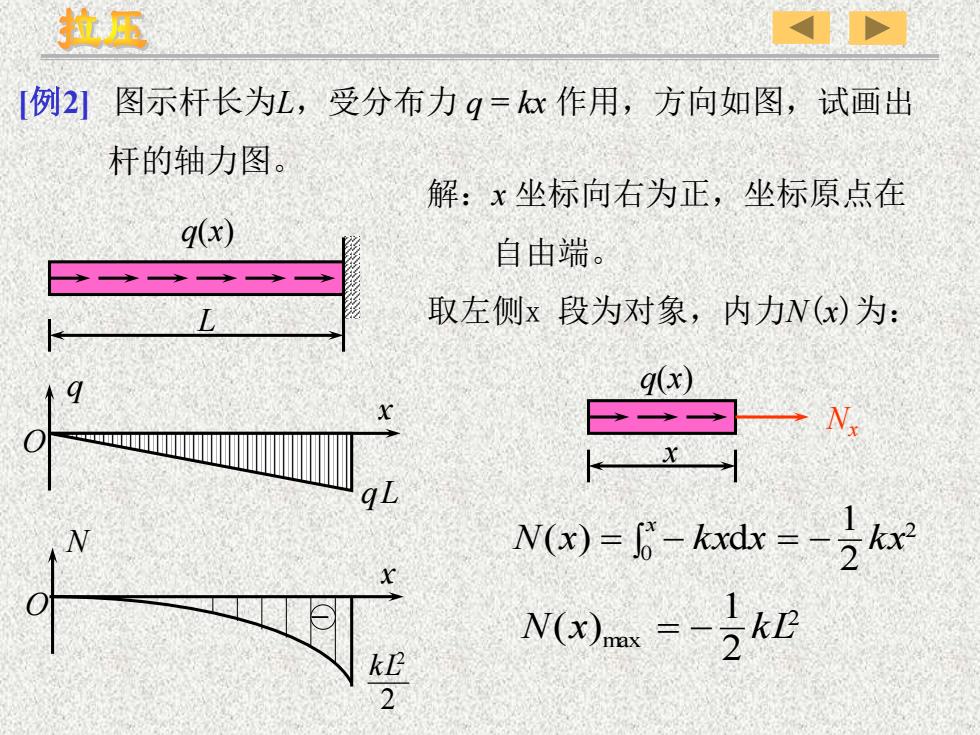
拉压[例2]图示杆长为L,受分布力 q=kx 作用,方向如图,试画出杆的轴力图。解:x坐标向右为正,坐标原点在q(x)自由端。取左侧x 段为对象,内力N(x)为:q(x)9xNx+福qlN(x) - l6- kxdx=-- kxNX10N(0).m--kkL2
解:x 坐标向右为正,坐标原点在 自由端。 取左侧x 段为对象,内力N(x)为: q qL x O 2 0 2 1 N(x) k xdx k x x = − = − 2 max 2 1 N(x) = − k L [例2] 图示杆长为L,受分布力 q = kx 作用,方向如图,试画出 杆的轴力图。 L q(x) Nx x q(x) N x O – 2 2 kL

拉压81-3香截面上的应力及强度条件问题提出:pPpP1.内力大小不能衡量构件强度的大小。2.强度:①内力在截面分布集度应力;②材料承受荷载的能力。应力的概念1.定义:由外力引起的内力集度
一、应力的概念 §1–3 截面上的应力及强度条件 问题提出: P P P P 1. 内力大小不能衡量构件强度的大小。 2. 强度:①内力在截面分布集度⎯应力; ②材料承受荷载的能力。 1. 定义:由外力引起的内力集度