
教案第十七章波动光学 容易明白:在双镜干涉实验中M和两平面镜上反射的两束光,虽然都发生了元 的跃变,但两者的光程差(或相位差)却不变。 劳埃德镜干涉实验的特点: 1.两束相干光由光源S和虚光源S发出: 2.两光源相位相同,可比作杨氏双缝干涉实验中的两个狭缝: 3.只有虚光源有半波损失: 4.重叠区形成条纹,条纹对两光源不对称。 S3光程薄膜干涉OpticalPath,Thin Film Interference 薄膜干涉:如阳光照射下的肥皂膜,水面上的油膜,蜻蜓、蝉等昆虫的翅膀上呈现 的彩色花纹,车床车削下来的钢铁碎屑上呈现的蓝色光谱等。 薄膜干涉的特点:厚度不均匀的薄膜表面上的等厚干涉和厚度均匀薄膜在无穷远出 形成的等倾干涉。 一光程 当两束光分别通过不同介质时,由于同一频率的光在不同介质中的传播速度不同, 因此不同介质中的光波波长不同。这时就不能只根据几何路程差来计算相位差了。为此, 引入光程的概念。 1.光程 分析:单色光振动频率在不同介质中 是不同的。 。在折射率为n的介质中,光速变为 V=cIn d ·介质中的波长变为”-上=2 v n 图17-5光程计算用图 因此在折射率为的某一介质中,如 果光波通过的几何路程为x,其间的波数为x/入',同样波数的光波在真空中通过的几何 路程将是: x/2'= 上式表明:光波在介质中传播时,其相位的变化不仅与光波传播的几何路程和真空 中的波长有关,而且还与介质的折射率有关。光的折射率为的介质中通过几何路程L所 发生的相位变化,相当于光在真空中通过L的路程所发生的相位变化。 276
教案 第十七章 波动光学 276 容易明白:在双镜干涉实验中 M1 和 M2 两平面镜上反射的两束光,虽然都发生了 的跃变,但两者的光程差(或相位差)却不变。 劳埃德镜干涉实验的特点: 1. 两束相干光由光源 S 和虚光源 S发出; 2. 两光源相位相同,可比作杨氏双缝干涉实验中的两个狭缝; 3. 只有虚光源有半波损失; 4. 重叠区形成条纹,条纹对两光源不对称。 §3 光程 薄膜干涉 Optical Path , Thin Film Interference 薄膜干涉:如阳光照射下的肥皂膜,水面上的油膜,蜻蜓、蝉等昆虫的翅膀上呈现 的彩色花纹,车床车削下来的钢铁碎屑上呈现的蓝色光谱等。 薄膜干涉的特点:厚度不均匀的薄膜表面上的等厚干涉和厚度均匀薄膜在无穷远出 形成的等倾干涉。 一 光程 当两束光分别通过不同介质时,由于同一频率的光在不同介质中的传播速度不同, 因此不同介质中的光波波长不同。这时就不能只根据几何路程差来计算相位差了。为此, 引入光程的概念。 1. 光程 分析:单色光振动频率在不同介质中 是不同的。 ⚫ 在折射率为n的介质中,光速变为 V = c / n ⚫ 介质中的波长变为 n V = = 因此在折射率为n的某一介质中,如 果光波通过的几何路程为x,其间的波数为 x / ,同样波数的光波在真空中通过的几何 路程将是: x / = nx 上式表明:光波在介质中传播时,其相位的变化不仅与光波传播的几何路程和真空 中的波长有关,而且还与介质的折射率有关。光的折射率为n的介质中通过几何路程L所 发生的相位变化,相当于光在真空中通过nL的路程所发生的相位变化。 …… …… d1 d2 d3 dm n1 n2 n3 nm 图 17-5 光程计算用图
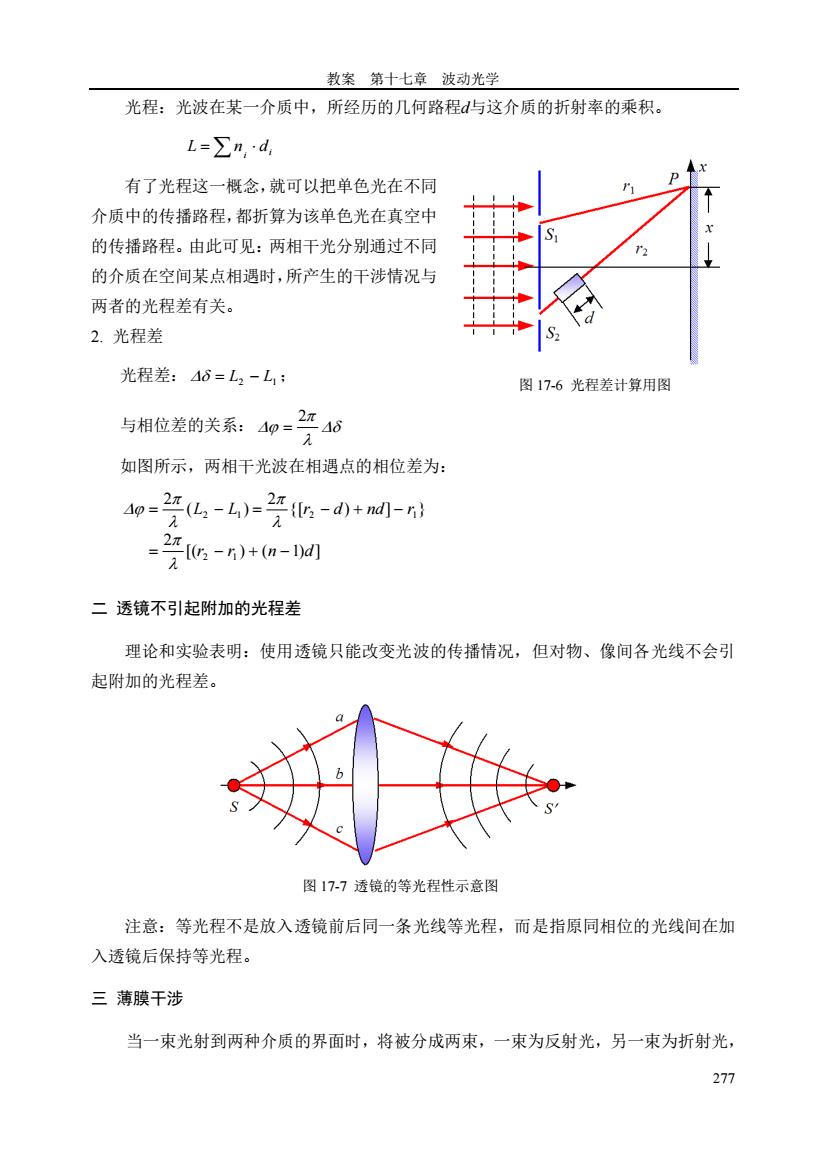
教案第十七章波动光学 光程:光波在某一介质中,所经历的几何路程d与这介质的折射率的乘积。 L=∑n,·d, 有了光程这一概念,就可以把单色光在不同 介质中的传播路程,都折算为该单色光在真空中 的传播路程。由此可见:两相干光分别通过不同 的介质在空间某点相遇时,所产生的干涉情况与 两者的光程差有关。 2.光程差 光程差:46=L2-L1: 图17-6光程差计算用图 与相位差的关系:4如一受40 如图所示,两相干光波在相遇点的相位差为: o=受化-=受-0+-d -7G-)+a-n 二透镜不引起附加的光程差 理论和实验表明:使用透镜只能改变光波的传播情况,但对物、像间各光线不会引 起附加的光程差。 图17-7透镜的等光程性示意图 注意:等光程不是放入透镜前后同一条光线等光程,而是指原同相位的光线间在加 入透镜后保持等光程。 三薄膜干涉 当一束光射到两种介质的界面时,将被分成两束,一束为反射光,另一束为折射光 277
教案 第十七章 波动光学 277 光程:光波在某一介质中,所经历的几何路程d与这介质的折射率的乘积。 i i L = n d 有了光程这一概念,就可以把单色光在不同 介质中的传播路程,都折算为该单色光在真空中 的传播路程。由此可见:两相干光分别通过不同 的介质在空间某点相遇时,所产生的干涉情况与 两者的光程差有关。 2. 光程差 光程差: = L2 − L1 ; 与相位差的关系: 2 = 如图所示,两相干光波在相遇点的相位差为: [( ) ( 1) ] 2 {[ ) ] } 2 ( ) 2 2 1 2 1 2 1 r r n d L L r d nd r = − + − = − = − + − 二 透镜不引起附加的光程差 理论和实验表明:使用透镜只能改变光波的传播情况,但对物、像间各光线不会引 起附加的光程差。 注意:等光程不是放入透镜前后同一条光线等光程,而是指原同相位的光线间在加 入透镜后保持等光程。 三 薄膜干涉 当一束光射到两种介质的界面时,将被分成两束,一束为反射光,另一束为折射光, 图 17-6 光程差计算用图 图 17-7 透镜的等光程性示意图

教案第十七章波动光学 从能量守恒的角度来看,反射光和折射光的振幅 都要小于入射光的振幅,这相当于振幅被“分割” 了。 两光线a,b在焦平面上P点相交时的光程 差 6=2en-misin2i+8' 8取决于m,m,的性质。由半波损失决定 的,等于0或分 图17-9海膜干涉光路 对于厚度均匀的薄膜,光程差是由入射角1决定 的,凡以相同的倾角入射的光,经膜的上、下表面反射 后产生的相关光束都有相同的光程差,从而对应于干涉 图样样中的一条条纹,故将此类干涉条纹称为等倾条纹。 等倾干涉明纹的光程差的条件: 6=2en2-nisin2i+6'=2k,(k=12,3,..) 图17-8等倾干涉条纹 等倾干涉暗纹的光程差的条件: 6=2e√m-nsin2i+8=(2k+1)2,(k=l,2,3) 两透射光线a,b'相干的光程差: 6=2en-nsin'i 透射光也有干涉现象。当反射光的干涉相互加强时,透射光的干涉相互减弱。显然, 这是符合能量守恒定律的。 反射光相互加强时透射光相互减弱,当反射光相交减弱时,透射光相互加强,两者是 互补的。 ·增透膜:膜的厚度适当时,可使某种波长的反射光因干涉而减弱,从而使更多的光 能透过元件。 ·增反膜(高反射膜):膜的厚度适当时,能使某些波长的反射光因为干涉而增强, 从而使某些波长的光更多地反射。 278
教案 第十七章 波动光学 278 从能量守恒的角度来看,反射光和折射光的振幅 都要小于入射光的振幅,这相当于振幅被“分割” 了。 两光线 a, b 在焦平面上P 点相交时的光程 差 = e n − n i + 2 2 1 2 2 2 sin 取决于n1, n2, n3的性质。由半波损失决定 的,等于 2 0 或 。 对于厚度均匀的薄膜,光程差是由入射角 i 决定 的,凡以相同的倾角入射的光,经膜的上、下表面反射 后产生的相关光束都有相同的光程差,从而对应于干涉 图样样中的一条条纹,故将此类干涉条纹称为等倾条纹。 等倾干涉明纹的光程差的条件: 2 sin 2 ( 1,2,3, ) 2 2 1 2 = e n2 − n i + = k, k = 等倾干涉暗纹的光程差的条件: 2 sin (2 1) ( 1,2,3, ) 2 2 1 2 = e n2 − n i + = k + , k = 两透射光线 a, b 相干的光程差: e n n i 2 2 1 2 2 = 2 − sin 透射光也有干涉现象。当反射光的干涉相互加强时,透射光的干涉相互减弱。显然, 这是符合能量守恒定律的。 反射光相互加强时透射光相互减弱,当反射光相交减弱时,透射光相互加强,两者是 互补的。 ⚫ 增透膜:膜的厚度适当时,可使某种波长的反射光因干涉而减弱,从而使更多的光 能透过元件。 ⚫ 增反膜(高反射膜):膜的厚度适当时,能使某些波长的反射光因为干涉而增强, 从而使某些波长的光更多地反射。 a b i S b 薄膜 a n1 n2 n3 图 17-9 薄膜干涉光路图 图 17-8 等倾干涉条纹

教案第十七章波动光学 S4劈尖牛顿环Pointed Split,Newton's Ring 当一束平行光入射到厚度不均匀的透明介质薄膜上,如图所示,两光线1和b:的 光程差 6=2mecosy+8'=2en-mi sin2i+6' 当1保持不变时,光程差仅与膜的厚度有关,凡厚度相同的地方光程差相同,从而 对应同一条干涉条纹,将此类干涉条纹成为等厚干涉条纹。观察等厚干涉常用劈尖和牛 顿环。 实际应用中,通常使光线垂直入射膜面, 即1=y=0,光程差公式简化为 6=2ne+8 为此,明纹和暗纹出现的条件为 「 k=1,2,…,明纹 6=2n2e+8= 2k+ k=12,…,暗纹 一劈尖 劈尖是指,薄膜两表面互不平行,且成很小角度的劈形膜。当用平行光垂直照射折 射率为n2的劈尖时(1=0),由于劈角限小,所以在劈尖的上表面处反射的光线和在劈 尖下表面处反射的光线都可以看作垂直于劈尖表面,它们在劈尖表面处相遇并干涉。 劈尖干涉时的光程差公式为: 「k以 k=12,…,明纹 6=2n:e+6"=(2k+片k=l2,暗纹 设相邻明纹或暗纹之间劈形膜的厚度差为△e Ne=em-e=2m △e=1sm8≈le 1=2n0 279
教案 第十七章 波动光学 279 §4 劈尖 牛顿环 Pointed Split, Newton's Ring 当一束平行光入射到厚度不均匀的透明介质薄膜上,如图所示,两光线 a1 和b1 的 光程差 n e + = e n − n i + 2 2 1 2 2 2 2 cos 2 sin 当 i 保持不变时,光程差仅与膜的厚度有关,凡厚度相同的地方光程差相同,从而 对应同一条干涉条纹,将此类干涉条纹成为等厚干涉条纹。观察等厚干涉常用劈尖和牛 顿环。 实际应用中,通常使光线垂直入射膜面, 即 i = =0,光程差公式简化为 = n e + 2 2 为此,明纹和暗纹出现的条件为 + = = = + = 暗纹 明纹 1,2, , 2 (2 1) 1,2, , 2 2 k k k k n e 一 劈尖 劈尖是指,薄膜两表面互不平行,且成很小角度的劈形膜。当用平行光垂直照射折 射率为 n2 的劈尖时(i =0),由于劈角很小,所以在劈尖的上表面处反射的光线和在劈 尖下表面处反射的光线都可以看作垂直于劈尖表面,它们在劈尖表面处相遇并干涉。 劈尖干涉时的光程差公式为: + = = = + = 暗纹 明纹 1,2, , 2 (2 1) 1,2, , 2 2 k k k k n e 设相邻明纹或暗纹之间劈形膜的厚度差为 e n e e e k k 2 1 = + − = e = lsin l n l 2 =

教案第十七章波动光学 其中:为相邻两明(暗)条纹间距:n为劈尖介质的折射率:1为光在真空中的波长。 第级暗条纹第k+1级暗条纹 图17-9劈尖的干涉 结论:相邻两明(暗)纹处劈尖的厚度差为光在该介质中波长的12:而相邻的明、 暗纹处的厚度差为光在劈尖介质中的波长的14。干涉图样为一系列平行、等间距的明暗 相间的条纹。 讨论:在劈尖干涉装置中,如保持其劈角0不变,而膜的厚度增大或减薄,条纹将 怎样变化?劈尖增大,条纹又如何变化? 答:如町住某一干涉条纹看,将看到条纹明暗交替变化,但条纹间距不变,从整个 条纹看,如厚度增大向劈尖移动,如厚度减薄则远离劈尖。同理,当日增大时,条纹间 距变小,干涉条纹向劈尖移动。 二牛顿环 如图所示牛顿环实验装置示意图。一块曲率半径很大的平凸透镜与一平玻璃相接触 构成一个上表面为球面,下表面为平面的空气劈尖。由单色光源$发出的光,经半透半反 镜M反射后,垂直射向空气劈尖并在劈尖空气层的上下表面处反射,从而在显微镜T内可 观察到如图所示的干涉条纹图样。由于这里空气劈尖的等厚轨迹是以接触点为圆心的一 系列同心圆,所以干涉条纹的形状也是明暗相间的同心圆环。 280
教案 第十七章 波动光学 280 其中:l为相邻两明(暗)条纹间距;n为劈尖介质的折射率;为光在真空中的波长。 结论:相邻两明(暗)纹处劈尖的厚度差为光在该介质中波长的1/2;而相邻的明、 暗纹处的厚度差为光在劈尖介质中的波长的1/4。干涉图样为一系列平行、等间距的明暗 相间的条纹。 讨论:在劈尖干涉装置中,如保持其劈角 不变,而膜的厚度增大或减薄,条纹将 怎样变化?劈尖增大,条纹又如何变化? 答:如盯住某一干涉条纹看,将看到条纹明暗交替变化,但条纹间距不变,从整个 条纹看,如厚度增大向劈尖移动,如厚度减薄则远离劈尖。同理,当 增大时,条纹间 距变小,干涉条纹向劈尖移动。 二 牛顿环 如图所示牛顿环实验装置示意图。一块曲率半径很大的平凸透镜与一平玻璃相接触, 构成一个上表面为球面,下表面为平面的空气劈尖。由单色光源S发出的光,经半透半反 镜M反射后,垂直射向空气劈尖并在劈尖空气层的上下表面处反射,从而在显微镜T内可 观察到如图所示的干涉条纹图样。由于这里空气劈尖的等厚轨迹是以接触点为圆心的一 系列同心圆,所以干涉条纹的形状也是明暗相间的同心圆环。 图 17-9 劈尖的干涉