
①割集能够把图恰好分成两部分的一个支路集 合,但只要少移去此支路集合中的任一支路, 结束 则图仍是而且必须是联通的。 ②基本割集及其个数 只含有一个树枝的割集称为单树枝割集或基本割集。 基本割集的数目等于树枝的数目,即-1个 ③基本割集的编号及其参考方向规定基本割 集的编号顺序一般都取为与树枝的编号顺序一 致,其参考方向规定为该基本割集中含树枝的 参考方向。 2025-4-2 11
结束 ① 割集 能够把图恰好分成两部分的一个支路集 合,但只要少移去此支路集合中的任一支路, 则图仍是而且必须是联通的。 ② 基本割集及其个数 只含有一个树枝的割集称为单树枝割集或基本割集。 基本割集的数目等于树枝的数目,即n-1个 ③ 基本割集的编号及其参考方向规定 基本割 集的编号顺序一般都取为与树枝的编号顺序一 致,其参考方向规定为该基本割集中含树枝的 参考方向。 2025-4-2 11

§15-2关联矩阵、回路矩阵、割集矩阵 结束 1.图的矩阵表示 图的矩阵表示是指用矩阵描述图的拓扑性质, 即KCL和KVL的矩阵形式。有三种矩阵形式: 结点 支路 关联矩阵A 回路 一 支路 回路矩阵B 割集 支路 割集矩阵Q 2025-4-2 12
§ 结束 15-2 关联矩阵、回路矩阵、割集矩阵 图的矩阵表示是指用矩阵描述图的拓扑性质, 即KCL和KVL的矩阵形式。有三种矩阵形式: 1. 图的矩阵表示 结点 支路 关联矩阵A 回路 支路 回路矩阵B 割集 支路 割集矩阵Q 2025-4-2 12

2.关联矩阵A 结束 用矩阵形式描述结点和支路的关联性质。n个 结点b条支路的图用nxb的矩阵描述: 支路b 乡注意 结 A n×b 每一行对应一个结点, n 每一列对应一条支路。 矩阵A,的每一个元素定义为: 4k=1支路k与结点j关联,方向背离结点; 0' 4k=-1支路k与结点j关联,方向指向结点; ak=0支路k与结点j无关。 2025-4-2 13
结束 2. 关联矩阵A 用矩阵形式描述结点和支路的关联性质。n个 结点b条支路的图用nb的矩阵描述: Aa = n b 支路b 结 点 n 每一行对应一个结点, 每一列对应一条支路。 矩阵Aa的每一个元素定义为: 注意 ajk ajk=1 支路 k 与结点 j 关联,方向背离结点; ajk= -1 支路 k 与结点 j 关联,方向指向结点; ajk=0 支路 k 与结点 j 无关。 2025-4-2 13
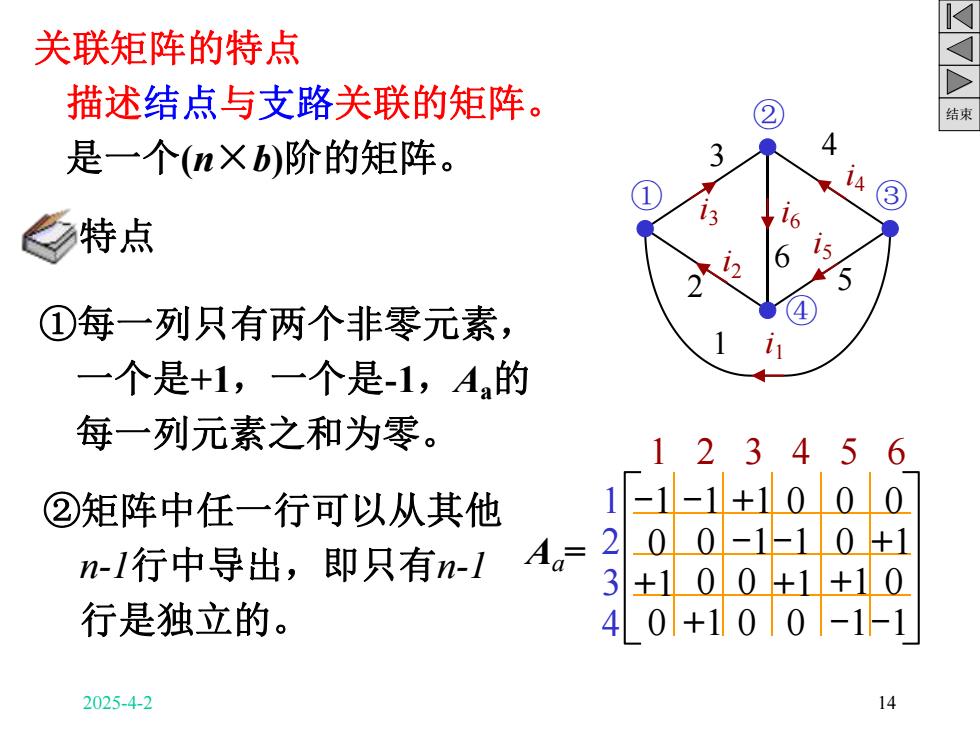
关联矩阵的特点 描述结点与支路关联的矩阵。 2 结束 是一个(nXb)阶的矩阵。 14③ 特点 15 5 ①每一列只有两个非零元素, 4 i 一个是+1,一个是-1,A的 每一列元素之和为零。 12 3456 ②矩阵中任一行可以从其他 1「-1-1+1000 n-1行中导出,即只有n-1 A。= 2 00-1-10+1 3+100+1+10 行是独立的。 40+100-1-1 2025-4-2 14
结束 关联矩阵的特点 描述结点与支路关联的矩阵。 是一个(n×b)阶的矩阵。 Aa = 1 2 3 4 1 2 3 4 5 6 -1 -1 +1 0 0 0 0 0 -1-1 0 +1 1 i1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④ +1 0 0 +1 +1 0 0 +1 0 0 -1-1 特点 ①每一列只有两个非零元素, 一个是+1,一个是-1,Aa的 每一列元素之和为零。 ②矩阵中任一行可以从其他 n-1行中导出,即只有n-1 行是独立的。 2025-4-2 14
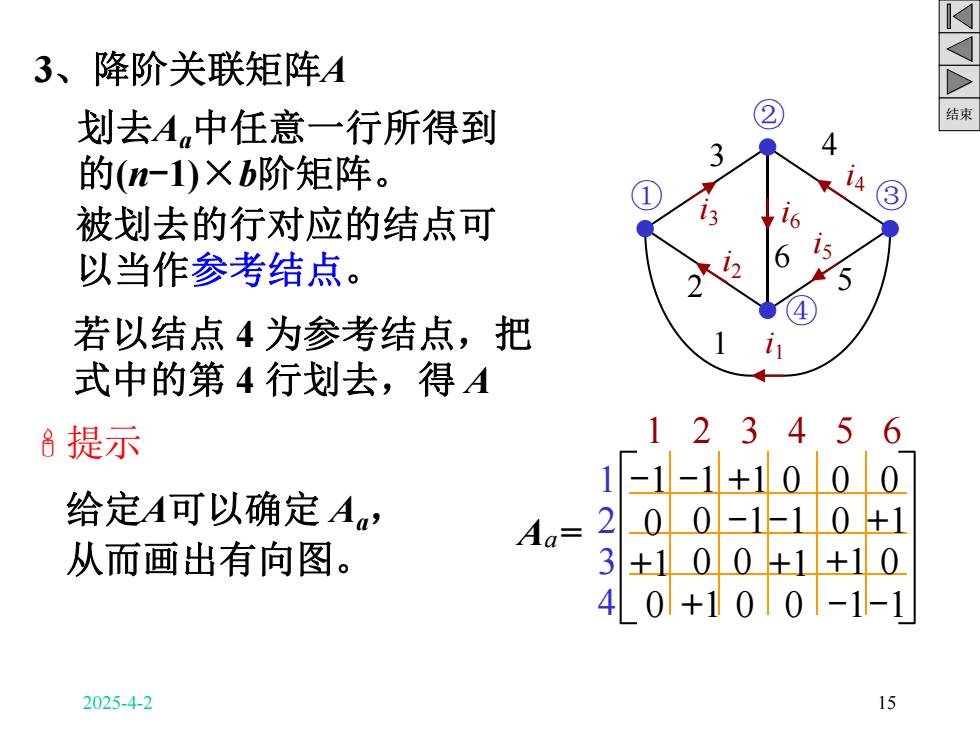
3、降阶关联矩阵A 划去A中任意一行所得到 2 结束 4 的(n-1)Xb阶矩阵。 i4③ 被划去的行对应的结点可 以当作参考结点。 5 若以结点4为参考结点,把 式中的第4行划去,得A 8提示 123456 1「-1-1+1000 给定A可以确定A, Aa=200-10+1 从而画出有向图。 3100+1+10 40+100-1-1 2025-4-2 15
结束 3、降阶关联矩阵A 划去Aa中任意一行所得到 的(n-1)×b阶矩阵。 A = 1 2 3 4 1 2 3 4 5 6 -1 -1 +1 0 0 0 0 0 -1-1 0 +1 +1 0 0 +1 +1 0 0 +1 0 0 -1-1 被划去的行对应的结点可 以当作参考结点。 a ' 提示 给定A可以确定 Aa, 从而画出有向图。 若以结点 4 为参考结点,把 式中的第 4 行划去,得 A 1 i1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④ 2025-4-2 15