全移,G一分为二;少移一条,G连通。 06 结束 a (b,d,e,f)是 (a,e,c,f)是 (a,b,c,d)也是 (ad,e,f)不是G的割集! 原因:少移去e,G仍为两部分。 2025-4-2 6
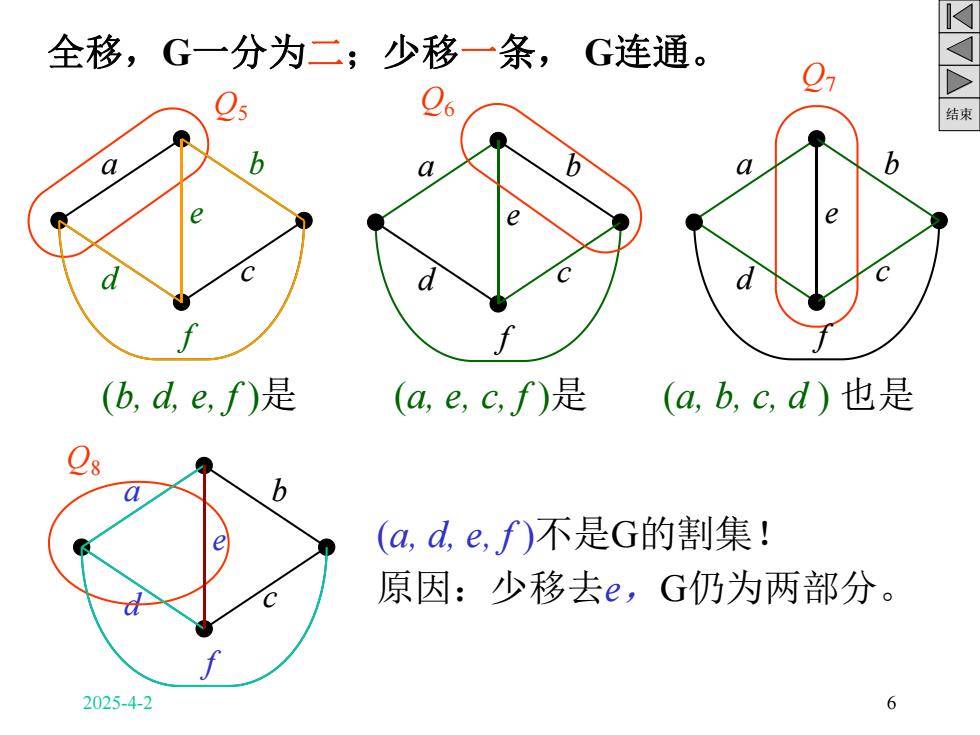
结束 全移,G一分为二;少移一条, G连通。 (b, d, e, f )是 (a, d, e, f )不是G的割集! Q5 a d f b c e a d f b c e Q6 Q7 a d f b c e a d f b c e Q8 (a, e, c, f )是 (a, b, c, d ) 也是 原因:少移去e,G仍为两部分。 2025-4-2 6
(a,b,c,d,e)不是G的割集! 原因:全移,G被分为三部分。 结束 2.割集的判断与确定 直观方便的方法是闭合面加定义。 注意:有些割集可能不易用与 闭合面相切割的方法表示。 无法作闭合面判断 与Q相切割的支路集 割集(a,b,C,)。 合(a,b,e)不是割集。 2025-4-2
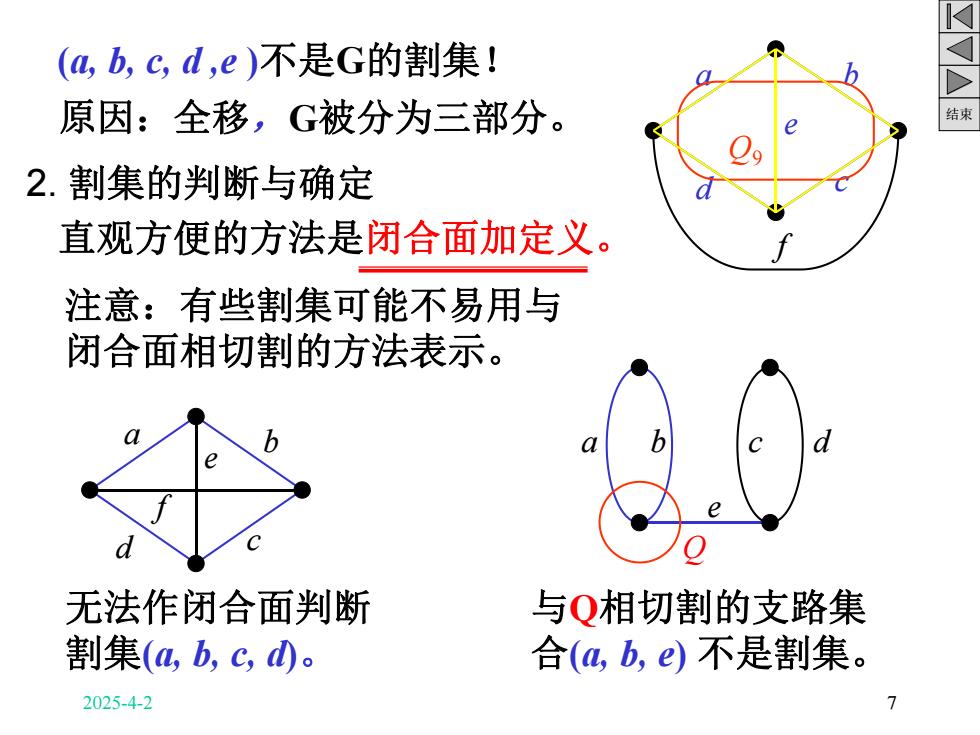
结束 (a, b, c, d ,e )不是G的割集! 原因:全移,G被分为三部分。 2. 割集的判断与确定 直观方便的方法是闭合面加定义。 a d f b c e Q9 注意:有些割集可能不易用与 闭合面相切割的方法表示。 a b e c d f 无法作闭合面判断 割集(a, b, c, d)。 Q a b c d e 与Q相切割的支路集 合(a, b, e) 不是割集。 2025-4-2 7

3.独立割集和基本割集 KCL适用于任一闭合面。 结束 8属同一割集的所有支路电 流也满足KCL。 ◆对于一个连通图G,总 可以列出与割集数量相 当割集的所有支路连接 等的KCL方程。但它们 于同一结点时,割集的 不一定线性独立。 KCL变为结点的KCL。 ()独立割集 对较大规模的电路,用 与一组线性独立的KCL 观察法选择一组独立割 方程相对应的割集,称 集是困难的。 为独立割集。 借助于树,就比较方便。 2025-4-2
结束 3. 独立割集和基本割集 KCL适用于任一闭合面。 ' 属同一割集的所有支路电 流也满足KCL。 对于一个连通图 G,总 可以列出与割集数量相 等的KCL方程。但它们 不一定线性独立。 (1)独立割集 与一组线性独立的KCL 方程相对应的割集,称 为独立割集。 a b e c d f Q1 Q2 Q3 Q4 当割集的所有支路连接 于同一结点时,割集的 KCL变为结点的KCL。 对较大规模的电路,用 观察法选择一组独立割 集是困难的。 借助于树,就比较方便。 2025-4-2 8
4.独立割集的确定 选一个树,一条树支 结束 与相应的连支可以构 成一个割集。 由一条树支与相应的连 支构成的割集叫单树支 割集。 而基本割集组是独 立割集组。 对于具有n个结点b条支 路的连通图,树支数为 独立割集组不一 n-1)条。 定是单树支割集。 就象独立回路不 这(-1)个单树支割集称 一定是单连支回 为基本割集组。 路一样。 2025-4-2 9
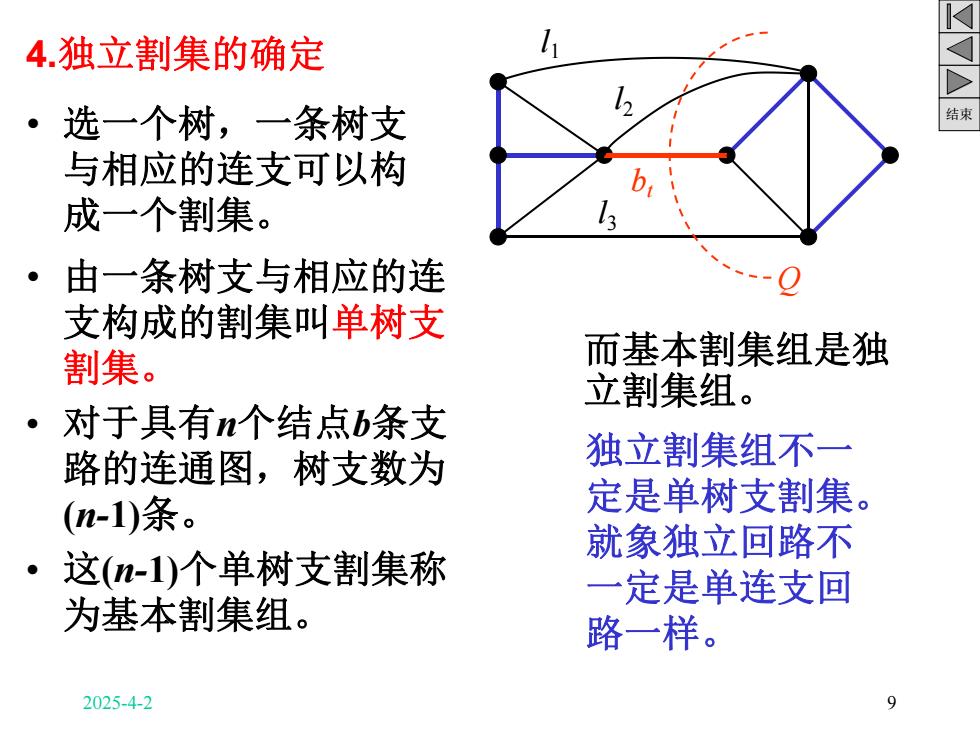
结束 4.独立割集的确定 • 选一个树,一条树支 与相应的连支可以构 成一个割集。 • 由一条树支与相应的连 支构成的割集叫单树支 割集。 • 对于具有n个结点b条支 路的连通图,树支数为 (n-1)条。 • 这(n-1)个单树支割集称 为基本割集组。 bt l1 l2 l3 Q 独立割集组不一 定是单树支割集。 就象独立回路不 一定是单连支回 路一样。 而基本割集组是独 立割集组。 2025-4-2 9
树支为2,3,4,6时的基本割集组 结束 02 Q1(1,2,5,7,8) 02(1,3,5,8) 93(1,4,5) Q4(5,6,7,8) 树支为 同一个图,有 5,6,7,8 02 许多不同的树, 时的基 因此能选出许 本割集 多不同的基本 组。 割集组。 2025-4-2 10
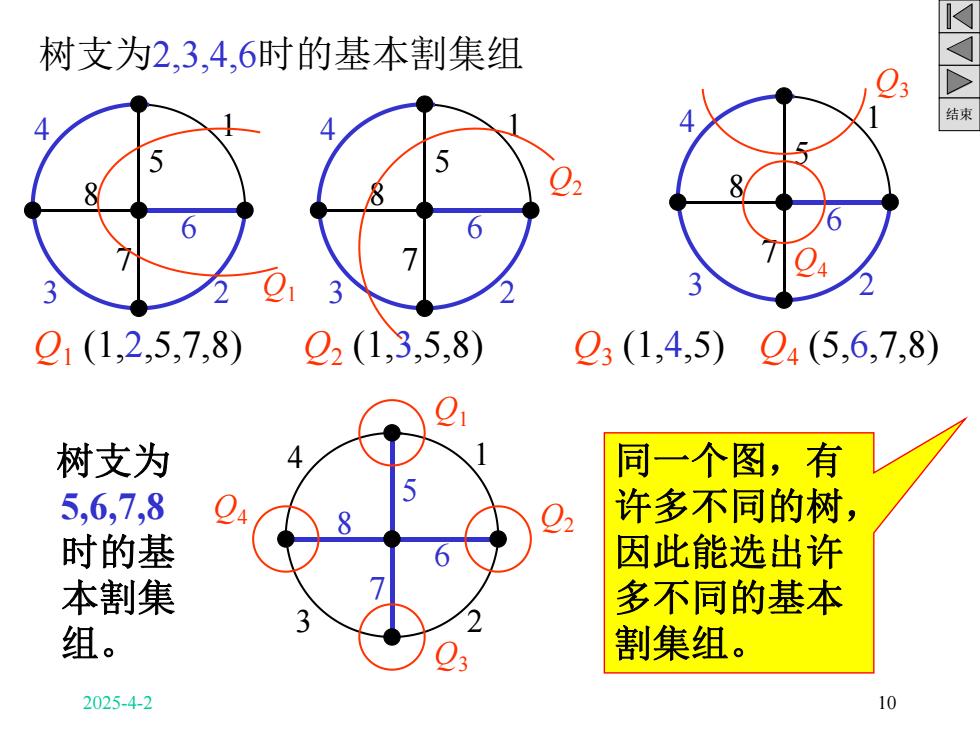
结束 树支为2,3,4,6时的基本割集组 树支为 5,6,7,8 时的基 本割集 组。 1 3 2 4 5 6 7 8 Q1 Q1 (1,2,5,7,8) 1 3 2 4 5 6 7 8 Q2 Q2 (1,3,5,8) 1 3 2 4 5 6 7 8 Q3 Q3 (1,4,5) Q4 Q4 (5,6,7,8) 1 3 2 4 5 6 7 8 Q1 Q2 Q3 Q4 同一个图,有 许多不同的树, 因此能选出许 多不同的基本 割集组。 2025-4-2 10