
考虑到不同能带的电子,晶体中电子速度的一般表述: U.()=VE,(K) 这个公式表达了一个非常重要的事实,那就是: 晶体中电子的平均速度只与能量和波矢有关,对时间和 空间而言,它是常数,因此平均速度将永远保持不变而不衰 减。也就是说可以一直流动下去而不衰减。这意味着:电子 不会被静止的原子所散射,严格周期性的晶体电阻率为零。 这一点和自由电子论中离子是作为散射中心对电子产生 散射而影响电子的平均(漂移)速度的概念完全不同。 下一节还将仔细分析这种情况
考虑到不同能带的电子,晶体中电子速度的一般表述: ( ) 1 (k ) E k n k n v h v u = Ñv 这个公式表达了一个非常重要的事实,那就是: 晶体中电子的平均速度只与能量和波矢有关,对时间和 空间而言,它是常数,因此平均速度将永远保持不变而不衰 减。也就是说可以一直流动下去而不衰减。这意味着:电子 不会被静止的原子所散射,严格周期性的晶体电阻率为零。 这一点和自由电子论中离子是作为散射中心对电子产生 散射而影响电子的平均(漂移)速度的概念完全不同。 下一节还将仔细分析这种情况

换句话说:若电子处于一个确定的状态Ψk时,只要晶格 的周期性不变,则永远处于这个态,因此,只要这种情况 不变,则电子将以同样的速度在整个晶体中不断运动,而 不被任何晶格所阻碍,即电子速度是一个常数,因为晶格 对传播速度的影响,都已经通过能量E,(k)包括在内了。 当然,晶格对周期性的偏离会引起电子的散射,使它 的速度发生变化,例如,电子在热振动的晶格中运动,会 和声子多次碰撞,对电子的速度产生极大影响:此外,外 加电场和磁场也会对电子运动速度带来变化,以后将陆续 讨论到这些情况
换句话说:若电子处于一个确定的状态 时,只要晶格 的周期性不变,则永远处于这个态,因此,只要这种情况 不变,则电子将以同样的速度在整个晶体中不断运动,而 不被任何晶格所阻碍,即电子速度是一个常数,因为晶格 对传播速度的影响,都已经通过能量 包括在内了。 当然,晶格对周期性的偏离会引起电子的散射,使它 的速度发生变化,例如,电子在热振动的晶格中运动,会 和声子多次碰撞,对电子的速度产生极大影响;此外,外 加电场和磁场也会对电子运动速度带来变化,以后将陆续 讨论到这些情况。 yk ( ) E k n
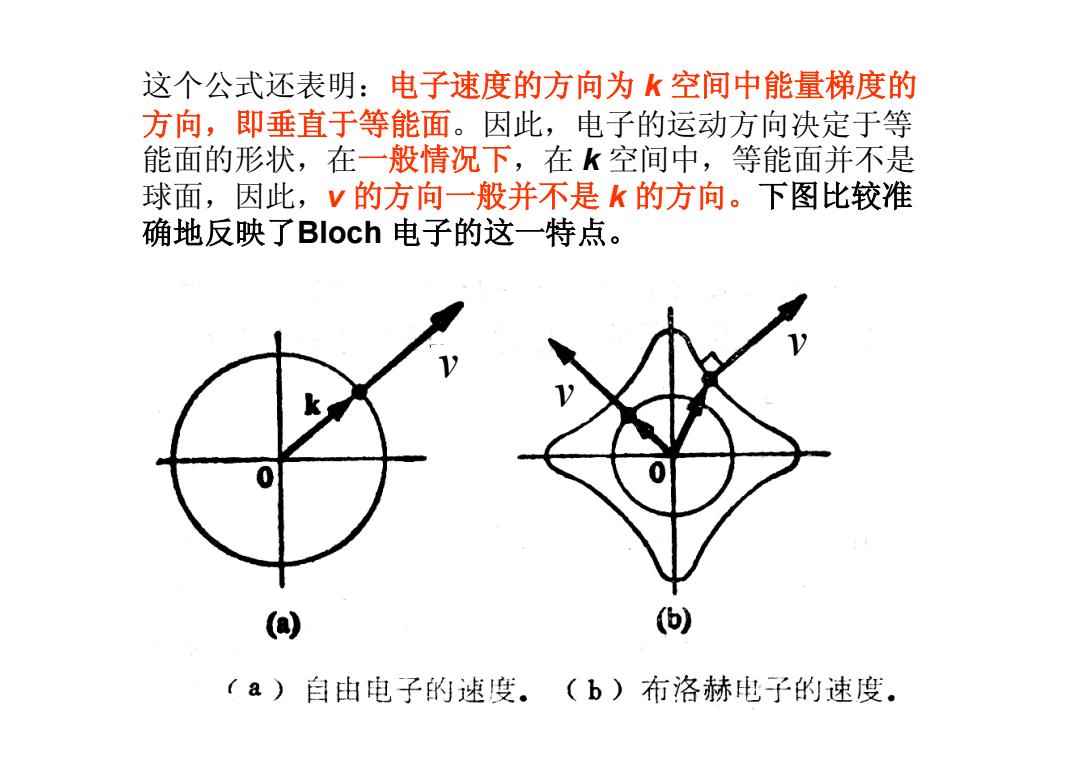
这个公式还表明:电子速度的方向为k空间中能量梯度的 方向,即垂直于等能面。因此,电子的运动方向决定于等 能面的形状,在一般情况下,在k空间中,等能面并不是 球面,因此,V的方向一般并不是k的方向。下图比较准 确地反映了Bloch电子的这一特点。 何) (a)自由电子的速度。(b)布洛赫电子的速度
这个公式还表明:电子速度的方向为 k 空间中能量梯度的 方向,即垂直于等能面。因此,电子的运动方向决定于等 能面的形状,在一般情况下,在 k 空间中,等能面并不是 球面,因此,v 的方向一般并不是 k 的方向。下图比较准 确地反映了Bloch 电子的这一特点。 v v v
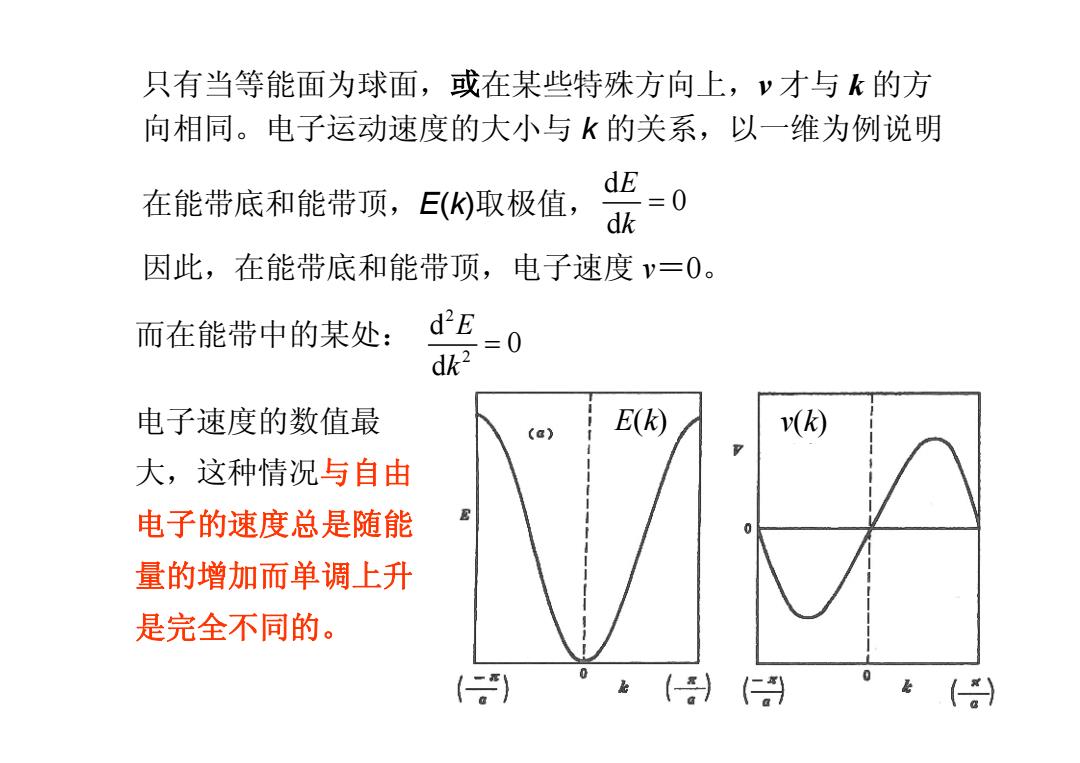
只有当等能面为球面,或在某些特殊方向上,y才与k的方 向相同。电子运动速度的大小与k的关系,以一维为例说明 dE 在能带底和能带项,E(K)取极值, =0 dk 因此,在能带底和能带顶,电子速度v=0。 而在能带中的某处: d"E =0 dk2 电子速度的数值最 (a) E() v(k) 大,这种情况与自由 电子的速度总是随能 0 量的增加而单调上升 是完全不同的。 。) 0)(。()
只有当等能面为球面,或在某些特殊方向上,v 才与 k 的方 向相同。电子运动速度的大小与 k 的关系,以一维为例说明 在能带底和能带顶,E(k)取极值, d 0 d E k = 因此,在能带底和能带顶,电子速度 v=0。 E(k) v(k) 而在能带中的某处: 电子速度的数值最 大,这种情况与自由 电子的速度总是随能 量的增加而单调上升 是完全不同的。 2 2 d 0 d E k =
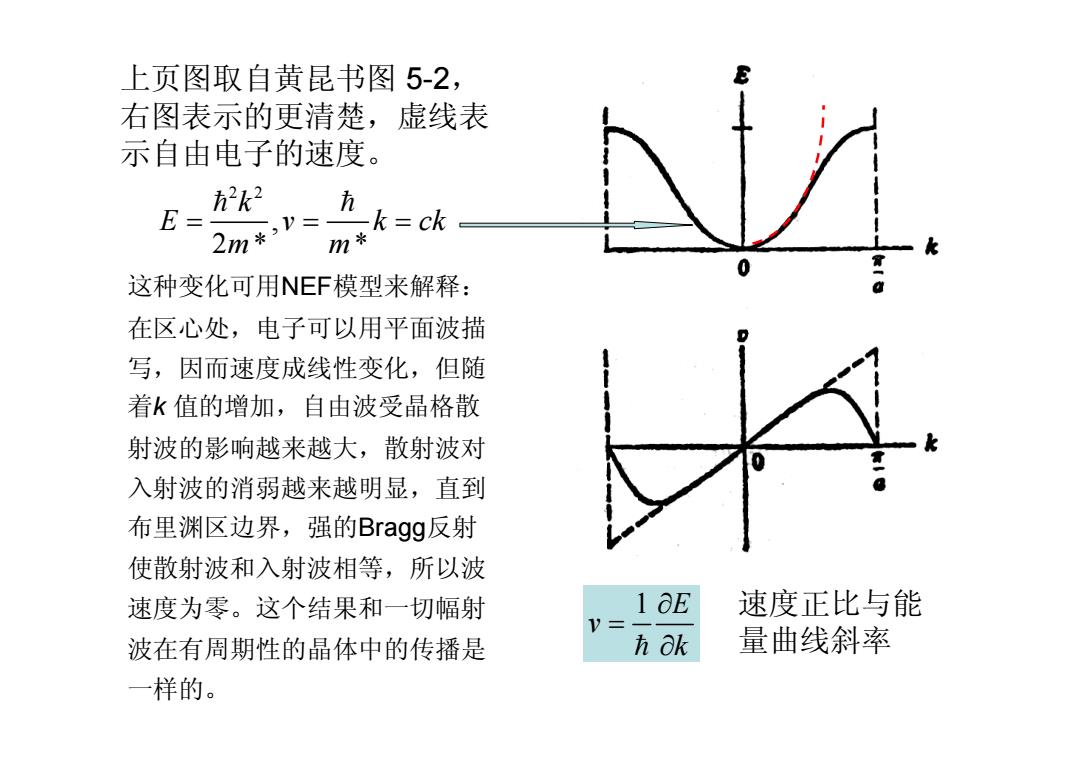
上页图取自黄昆书图5-2, 右图表示的更清楚,虚线表 示自由电子的速度。 2k2 E= k=ck m* 这种变化可用NEF模型来解释: 在区心处,电子可以用平面波描 写,因而速度成线性变化,但随 着k值的增加,自由波受晶格散 射波的影响越来越大,散射波对 入射波的消弱越来越明显,直到 布里渊区边界,强的Bragg反射 使散射波和入射波相等,所以波 速度为零。这个结果和一切幅射 1 aE 速度正比与能 V= 波在有周期性的晶体中的传播是 h Ok 量曲线斜率 一样的
上页图取自黄昆书图 5-2, 右图表示的更清楚,虚线表 示自由电子的速度。 这种变化可用NEF模型来解释: 在区心处,电子可以用平面波描 写,因而速度成线性变化,但随 着k 值的增加,自由波受晶格散 射波的影响越来越大,散射波对 入射波的消弱越来越明显,直到 布里渊区边界,强的Bragg反射 使散射波和入射波相等,所以波 速度为零。这个结果和一切幅射 波在有周期性的晶体中的传播是 一样的。 1 E v k ¶ = h ¶ 速度正比与能 量曲线斜率 2 2 , 2 * * k E v k ck m m = = = h h