
tu平(x.-e-u()iko0间 4(小eak 令为=k+5e0@服 e0-aaa四-l =4(x)ek 2sin{[x-(架)人] x-(架)
波包 ( ) ( ) ( ) 0 2 0 2 , d k k k i kx t k k x t e u x k w D D + - - Y = ò ( ) ( ) 0 2 0 0 2 d k k k i kx t k k u x e k w D D + - - » ò 令 0 k k = + x ( ) 0 0 d d k k k w w w x æ ö » + ç ÷ è ø ( ) ( ) ( ) 0 0 0 0 2 2 d , exp d d k k i k x t k k x t u x e i x t k w w x x D D - - ì ü ï ï é ù æ ö Y = - í ý ê ú ç ÷ ï ï ê ú è ø î þ ë û ò ( ) ( ) { ( ) } ( ) 0 0 0 0 0 2 2sin k i k x t k k k d dk d dk x t u x e x t w w w - D é ù - ë û = × - ( ) ( ) 0 k k u x » u x
为分析波包的运动,只需分析平2,即几率分布即可。 (w) sinw 竖w 波函数集中在尺度为 2 的范围内, △k 波包中心为:w=0。 2兀 0 2π W △K △k
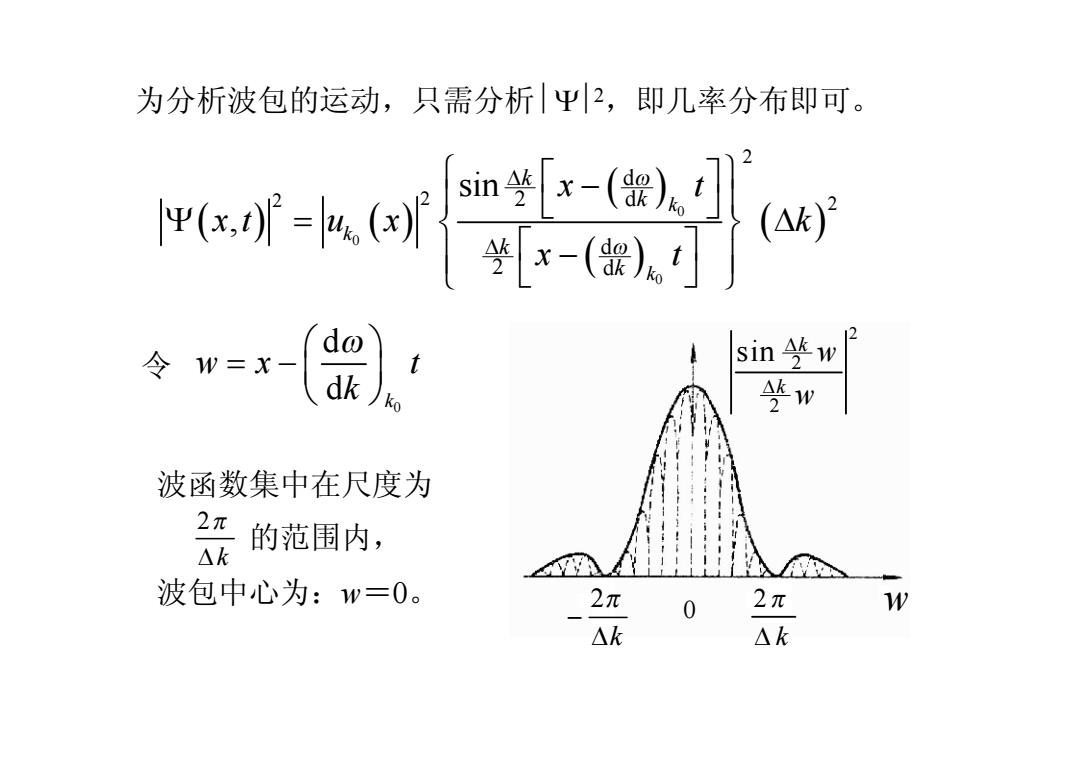
为分析波包的运动,只需分析 êYï2 ,即几率分布即可。 ( ) ( ) ( ) ( ) ( ) 0 0 0 2 2 2 2 d 2 d d 2 d sin , k k k k k k k x t x t u x k x t w w D D ì ü é ù - ï ï ë û Y = D í ý ï ï é ù - î þ ë û 令 0 d d k w x t k æ ö w = - ç ÷ è ø 2 w k p D 2 k p - D 0 2 2 2 sin k k w w D D 波函数集中在尺度为 的范围内, 波包中心为:w=0。 2 k p D

do 有 x= dk )ko dk )ko E(k)=ho(k) 若将波包看成一个准粒子,则粒子的速度为 ) 布里渊区的宽度:2π/,而假设△k很小,一般要求 .2π 即 2元 △k<< >>a a △k 推广到三维情况,电子速度为 V= VE 抗
有 0 0 d 1 d d d k k E x t t k k æ w ö æ ö = = ç ÷ ç ÷ è ø h è ø 若将波包看成一个准粒子,则粒子的速度为 ( ) 0 0 d 1 d d d k x E v k t k æ ö = = ç ÷ h è ø E(k k ) = hw ( ) 布里渊区的宽度:2p/a ,而假设 Dk 很小,一般要求 即 推广到三维情况,电子速度为 1 = Ñ E h k v a k 2p D << a k >> D 2p

注意,这里给出了把B引och波当作准经典粒子处理的条件。 由于B引och波有色散,一个稳定的波包所包含的波矢范围△k 应是一个很小的量。B引och波有独立物理意义的波矢被限制 在第一布里渊区内,△k<2π 因为测不准关系 a △px·△x=h△kx·△x≥ 2 .∴.△x>>a 这表明,如果波包的大小比原胞尺寸大得多,晶体中电子的 运动就可以用波包的运动规律来描述。对于输运现象,只有 当电子平均自由程远大于原胞尺寸的情况下,才可以把晶体 中的电子当作准经典粒子,波包移动的速度(群速度)等于 处于波包中心处粒子所具有的平均速度
注意,这里给出了把 Bloch 波当作准经典粒子处理的条件。 由于Bloch 波有色散,一个稳定的波包所包含的波矢范围△k 应是一个很小的量。Bloch 波有独立物理意义的波矢被限制 在第一布里渊区内, 因为测不准关系 2 x x Dp ×Dx = Dk x ×D ³ h h a k 2p D << \Dx a >> 这表明,如果波包的大小比原胞尺寸大得多,晶体中电子的 运动就可以用波包的运动规律来描述。对于输运现象,只有 当电子平均自由程远大于原胞尺寸的情况下,才可以把晶体 中的电子当作准经典粒子,波包移动的速度(群速度)等于 处于波包中心处粒子所具有的平均速度

附录:更简明的说明: 量子力学告诉我们,晶体中处于业状态的电子,在经 典近似下,其平均速度相当于以k为中心的波包速度,而 波包的传播速度是群速度:,_ω(k) VE= ak 量子力学中的德布罗意关系:E=o 所以电子的平均速度: p= 1 aE(k ak
附录:更简明的说明: 量子力学告诉我们,晶体中处于 状态的电子,在经 典近似下,其平均速度相当于以 k0为中心的波包速度,而 波包的传播速度是群速度: 量子力学中的德布罗意关系: 所以电子的平均速度: ( ) g k v k ¶w = ¶ E = hw 1 E k( ) v k ¶ = h ¶ 0 yk