
水人 新课 3.3.1线性相关性概念2 幸 定义3.3.对于向量组a4,a,a,若存在 m 个不全为零的数k,k,,km使得 kQ1+kQ2十…+kmm=0 (3.3.1) 则称向量组4,a2,,am线性相关 反过来,如果对于数kk…,km, k0必1+kQ2+…+kmQm=0台k1=k2=…=km=0, 就称向量组a,a,,a&n线性无关 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
以人 新课 3.3.1 线性相关性概念 2 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 m , , , 1 2 m m k , k , , k 1 2 定义3.3.1 对于向量组 ,若存在 个不全为零的数 使得 k1 1 + k2 2 ++ km m = 0 (3.3.1) 则称向量组 m , , , 1 2 线性相关 . 反过来,如果对于数 m k , k , , k 1 2 , k1 1 + k2 2 ++ km m = 0 k1 = k2 == km = 0 , 就称向量组 m , , , 1 2 线性无关

水人 新课 3.3.1线性相关性概念3 尚幸 由上述定义可知: (1)向量组只含一个向量Q时,a线性无关的 线性无关的充分必要条件是Q≠0因此,单个零 向量是线性相关的.进一步还可推出,包含零向量 的任何向量组都是线性相关的. 事实上,对于向量组,a2,…,0,,am,恒有 0a,+0a,+…+k0+…+0am=0,其中k可以是任意不为 零的数,故该向量组线性相关 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
以人 新课 3.3.1 线性相关性概念 3 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 时, 由上述定义可知: (1)向量组只含一个向量 线性无关的充分必要条件是 线性无关的 0 .因此,单个零 向量是线性相关的.进一步还可推出,包含零向量 的任何向量组都是线性相关的. 事实上,对于向量组 1 ,2 , ,0, , m 恒有 0 0 0 0 0, 1 + 2 ++ k ++ m = , 其中 k 零的数,故该向量组线性相关. 可以是任意不为
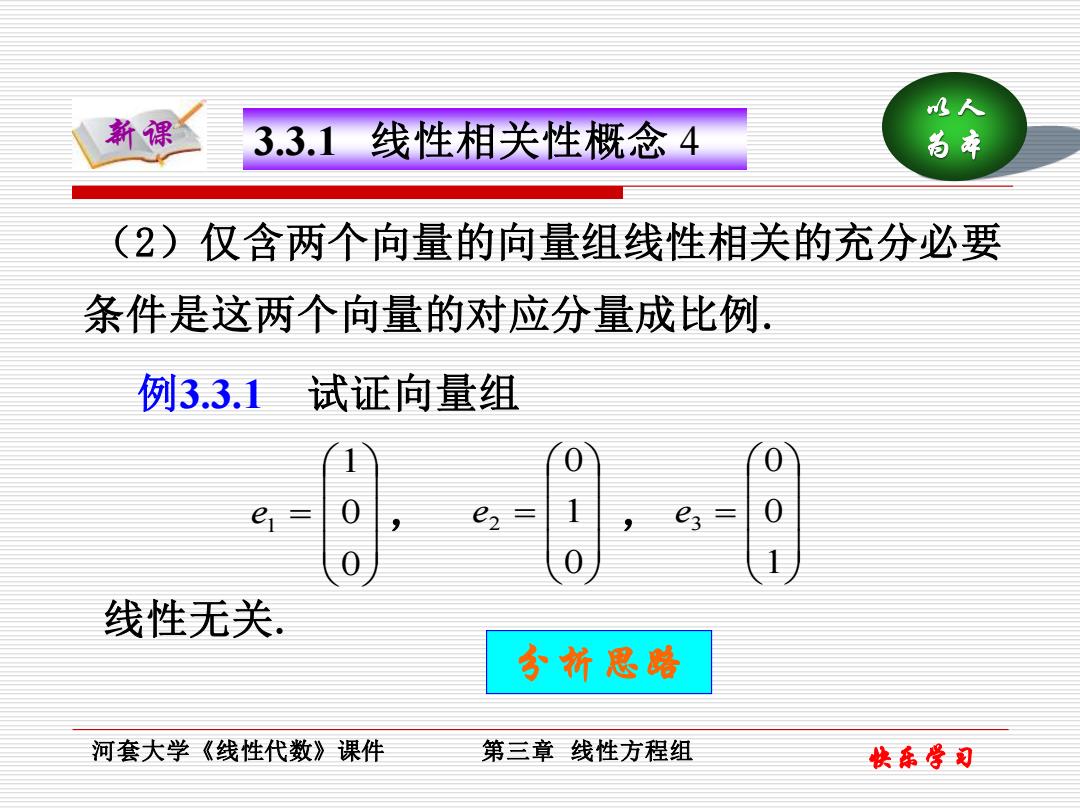
水人 新课 3.3.1线性相关性概念4 尚本 (2))仅含两个向量的向量组线性相关的充分必要 条件是这两个向量的对应分量成比例. 例33.1 试证向量组 三 e 0 线性无关 分折思哈 河套大学《线性代数》课件 第三章线性方程组 快乐学司
以人 新课 3.3.1 线性相关性概念 4 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 (2)仅含两个向量的向量组线性相关的充分必要 条件是这两个向量的对应分量成比例. 例3.3.1 试证向量组 = 0 0 1 1 e = 0 1 0 2 e = 1 0 0 3 , , e 线性无关. 分析思路
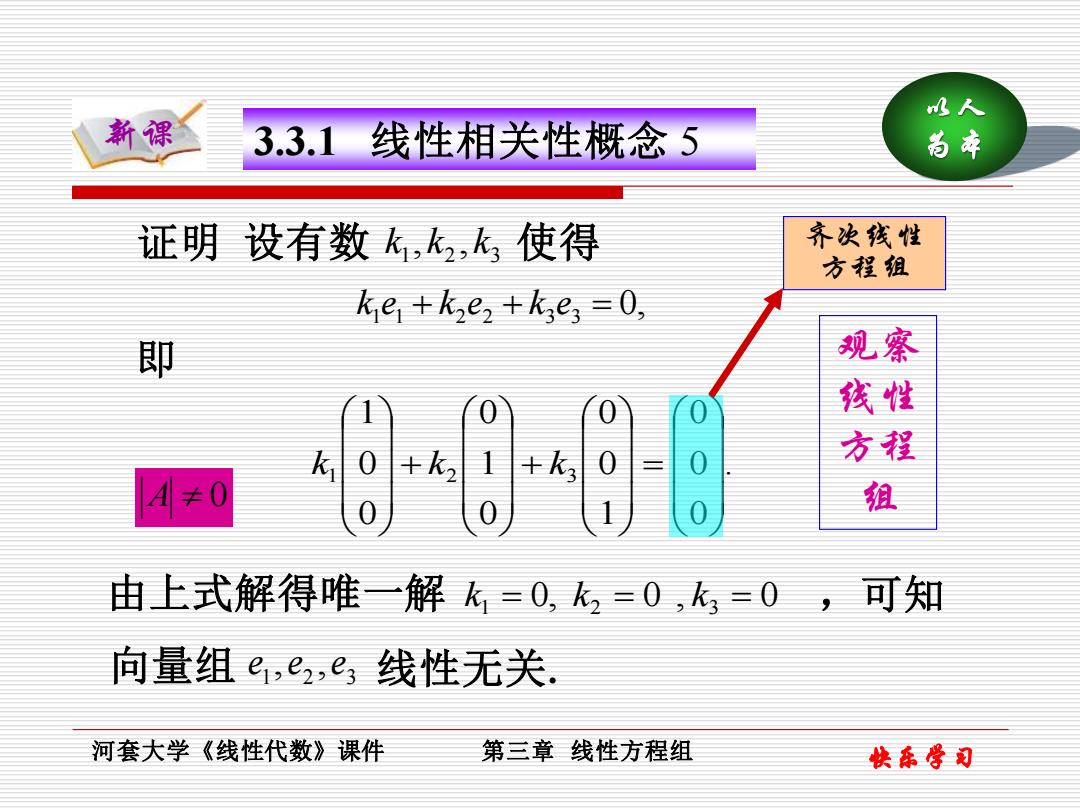
水人 新课 3.3.1线性相关性概念5 尚幸 证明设有数k,k2,k使得 齐次线性 方程组 k e +ke,+k;e;=0, 即 观察 0 线性 k 0 +k2 +k3 方程 4≠0 0 由上式解得唯一解k=0,k2=0,k3=0,可知 向量组,e2,e3线性无关. 河套大学《线性代数》课件 第三章线性方程组 快东学司
以人 新课 3.3.1 线性相关性概念 5 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 证明 设有数 1 2 3 k , k , k 使得 0, k1 e1 + k2 e2 + k3 e3 = . 0 0 0 1 0 0 0 1 0 0 0 1 1 2 3 = + + k k k 即 k1 = 0, k2 = 0 , k3 = 0 1 2 3 e , e , e 由上式解得唯一解 ,可知 向量组 线性无关. 观察 线性 方程 组 齐次线性 方程组 A 0

0人 新课 3.3.1线性相关性概念6 尚本 例33.2 给定向量组a,B,y,证明向量组 a,B,y线性无关的充分必要条件是a+B,B+y, y+a也线性无关 证明(秘要性)言 设有数k,k2,k,使得 k(@+B)+k(B+Y)+k(y+)=0, 整理即得 (k1+k3)Q+(k+k2)B+(k2+k3)y=0, 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
以人 新课 3.3.1 线性相关性概念 6 为本 河套大学《线性代数》课件 第三章 线性方程组 快乐学习 (k1 + k3 ) + (k1 + k2 ) + (k2 + k3 ) = 0 , 整理即得 , , , , + , + , 1 2 3 k , k , k 例3.3.2 给定向量组 ,证明向量组 线性无关的充分必要条件是 证明 (必要性) 设有数 ,使得 + 也线性无关. ( ) ( ) ( ) 0, k1 + + k2 + + k3 + =