
杉3X霜细直线AB,电荷线密度为入绕垂直于直线的轴0以角速度。匀速转动, 线形状不变,O点在AB延长线上)求O点的磁感应强度B和旋转带电线AB所形成的环 形电流的磁矩户。 d1-兴7话 o rtdr上带电 4T Adr R-冲=女 B-JaB= Lcatba] 02 (X年)Ξ r 4电流均匀地流过宽为2a的无限长平面导体薄板(板厚可略去不计),电流强度5元 通过板的中线并与板面垂直的平面上有一点P,P到板的垂直距离为y,如图所示,求P点的 磁感应强度B。 d虹-ia 2 dB dB≥.d边 MoIdx 起 4Tar B-SdBx=-SdBcoso 【o【oo60o十→X ←2a- 4Ta酚 9京 Hatxy 14 B=_
鼬 直线 1B,电荷线密度为λ绕垂直于直线的轴0以 角速度 ω匀速转动, ˇ `a ˉ ˇ 久 △… 叮 cJ〃 叨 ∷¨ ∷ ( ∷∷ ∶∷∷ 钅轩么华 J }`⌒亻劝`=£Ψ / 在 鸶 a∥‰bl ∵ ^J吖 ′丁J河 虍 舞 λ加 (线形状 霭克:F年 A:延苌纾 上)球 0点 的 【 感应强 秽 垂鸟黟繁::所彤冖即下 鼠 `冗:丝笋 ·召争 λ尻 ' P,P到 海体薄竣‰£豕荮葚r椠右,屡纛鸶篝 板的垂直距离为 y,如 图所示 ,求 P点的 ~以 〃 h 7 呷γ `∴ ∷∴Ⅱ∵~了 二石萨 i \ 弑 浇纭 ⊥ 一 彡招 幼j汪 I∶ 一‰ 祭 r久 ^ 钎 a⒅ V 一绎 呐 贪 ·14· ° 亠 〓冫 二 D幻 丿8 衤 0 -⒛ 颀 售争师妫争
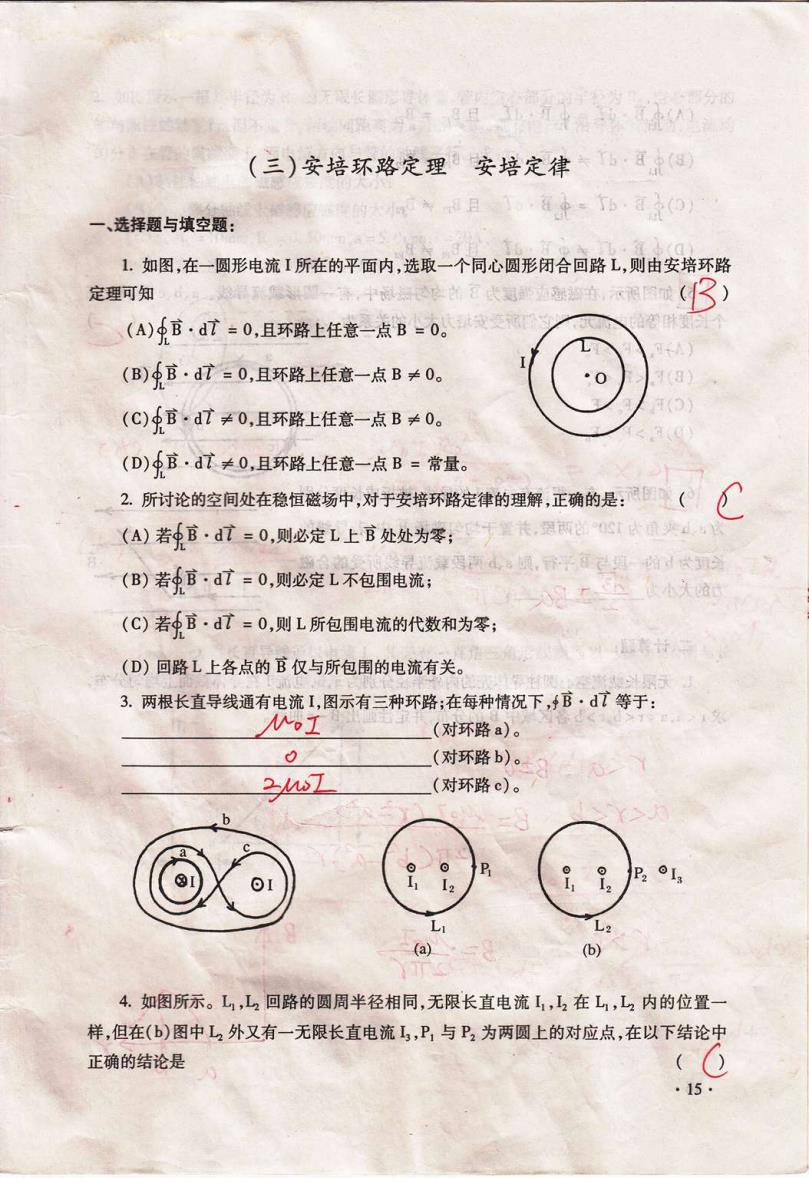
(三)安培环路定理安培定律 一、选择题与填空题: 1.如图,在一圆形电流I所在的平面内,选取一个同心圆形闭合回路L,则由安培环路 定理可知 中 的冠武司边缺语年,衣限的碳 3) (A)B·dt=0,且环路上任意-点B-0。发 (B)官·dt=0,且环路上任意-点B≠0。 ·0 (C)B,dt≠0,且环路上任意-点B≠0。 4(0 (D)少B·dt≠0,且环路上任意一点B=常量。 2 2.所讨论的空间处在稳恒磁场中,对于安培环路定律的理解,正确的是:( C (A)若官·d广=0,则必定L上官处处为零;天t,宽颗S类 年遇两4。顷,后平其的d代切 (B)若B·dt=0,则必定L不包围电流; (C)若官·dt=0,则L所包围电流的代数和为零; (D)回路L上各点的B仅与所包围的电流有关。 3.两根长直导线通有电流1,图示有三种环路;在每种情况下,B·dT等于: MoI (对环路a)。 0 (对环路b)。 2w7 (对环路c)。 (a) (b) 4.如图所示。L,L2回路的圆周半径相同,无限长直电流1,2在L,L2内的位置一 样,但在(b)图中L2外又有一无限长直电流L3,P,与P2为两圆上的对应点,在以下结论中 正确的结论是 ·15·
(三 )安培环路定理 安 培定律 ∷ 一、选择题与填空题: 1.如 图,在一圆形电流 I所在的平面内,选取一个同心圆形闭合回路 L,则 由安培环路 定理可知 ∷ (A)虫 j· 。σ 〓0,且环路上任啬一 点 o=o。 (:)兑官·d氵 〓0,且坏路上任意⊥点 B≠ 0。 I (C)兑言。d氵 ≠0,且环路上任意一点 B≠ 0。 (D)兑 官·d氵 ≠0,且坏路上任意一点 B〓 常量。 (B) 2.所讨论的空间处在稳恒磁场中,对于安培环路定律的理解,正确的是: ( (|)若∮ 言·d氵 〓0,则必定 L上 言处处为零; (B)若虫 言·J=0,贝刂必定 L不包围电流; (C)若虫 言·d氵 〓0,则 L所包围电流的代数和为零; (D)回 路 L上各点的言仅与所包围的电流有关。 3.两根长直导线通有电流 I,图示有三种环路;在每种情况下,∮ 言·d氵 等于 '伊 讠ェ (对环路a)。 (对环路b)。 ; 冖 (对环路 c)。 △ °凡 4.如 图所示。L1,△ 回路的圆周半径相同,无 限长直电流 I1,I2在 L1,△ 内的位置一 样,但在(b,图 中△外又有一无限长直电流 I3,P1与 Pz为 两圆上的对应点,在 以下结论中 (((∶∶1 ·15· L2 正确的结论是