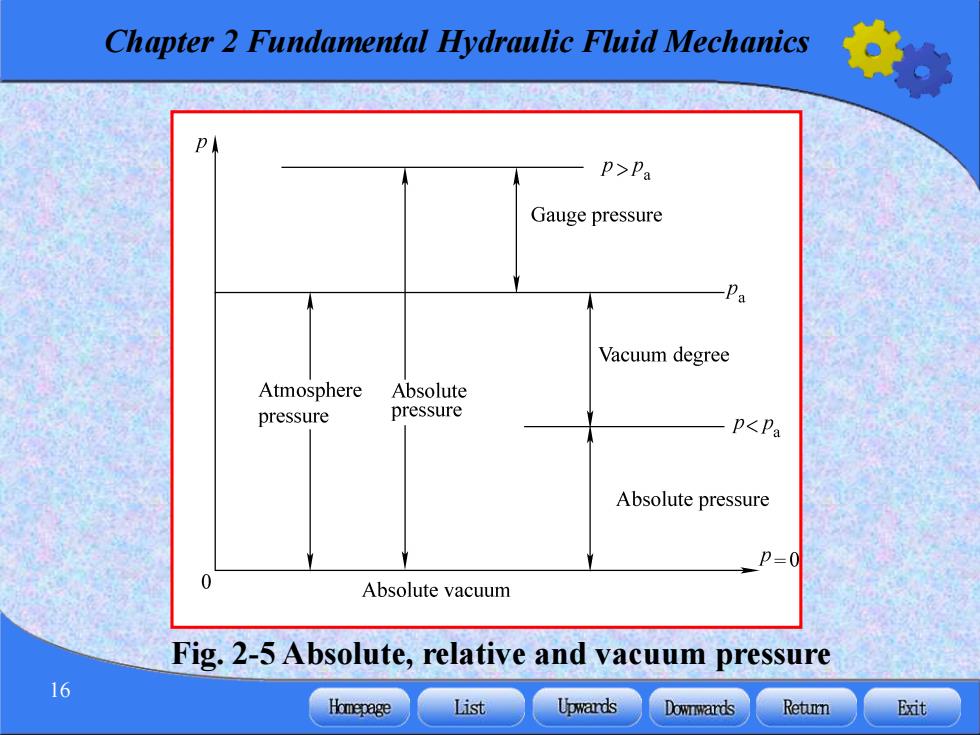
Chapter 2 Fundamental Hydraulic Fluid Mechanics p>Pa Gauge pressure Pa Vacuum degree Atmosphere Absolute pressure pressure p<Pa Absolute pressure Absolute vacuum Fig.2-5 Absolute,relative and vacuum pressure 16 Homepage List Upwards Downward达s Retumn Exit
Chapter 2 Fundamental Hydraulic Fluid Mechanics 16 Fig. 2-5 Absolute, relative and vacuum pressure

Chapter 2 Fundamental Hydraulic Fluid Mechanics Example 2-1:The oil is full in a container.For a given condition,the density of oil p=900kg/m3,the action force on this piston surface F=1000N, the area of piston A=1X103(m2),if the mass of piston is neglected,try to calculate the static pressurep at h=0.5m,as shown in Fig.2-6. Fig.2-6 Calculation of fluid static pressure 17 Homepage List Upwards Downwards Retumn Exit
Chapter 2 Fundamental Hydraulic Fluid Mechanics 17 Example 2-1: The oil is full in a container. For a given condition, the density of oil , the action force on this piston surface F=1000N, the area of piston A=1×10-3 (m2 ), if the mass of piston is neglected, try to calculate the static pressure p at h = 0.5m, as shown in Fig. 2-6. Fig. 2-6 Calculation of fluid static pressure 3 = 900kg/m

Chapter 2 Fundamental Hydraulic Fluid Mechanics 2.2.3 The principle of Pascal The principle of Pascal:pressure exerted on a confined liquid is transmitted undiminished in all directionsand acts with equal force on all equal areas. Its application is shown in Fig.2-7 A Fig.2-7 The example of Pascal principle 18 Homepage List Upwards Downwards Retumn Exit
Chapter 2 Fundamental Hydraulic Fluid Mechanics 18 2.2.3 The principle of Pascal The principle of Pascal: pressure exerted on a confined liquid is transmitted undiminished in all directions and acts with equal force on all equal areas. Its application is shown in Fig. 2-7. Fig. 2-7 The example of Pascal principle

Chapter 2 Fundamental Hydraulic Fluid Mechanics 2.2.4 Effect of fluid pressure on curved surfaces (1)When the wall is plane F=PA (2)When wall is a curved surface F=PA Example 2-2.Fig.2-8 shows a cylindrical member of inside radii r of length / Calculation:the effect force F on the right segment of the cylinder atx direction. d Fig.2-8 Effect force on the inner surface of the cylinder 19 Homepage List Upwards Downwards Retumn Exit
Chapter 2 Fundamental Hydraulic Fluid Mechanics 19 (1) When the wall is plane :F=PA (2) When wall is a curved surface : 2.2.4 Effect of fluid pressure on curved surfaces F pA x x = Example 2-2. Fig. 2-8 shows a cylindrical member of inside radii r of length . Calculation: the effect force Fx on the right segment of the cylinder at x direction. Fig. 2-8 Effect force on the inner surface of the cylinder l

Chapter 2 Fundamental Hydraulic Fluid Mechanics 2.3 Hydrodynamics 2.3.1 Equation of continuity-conservation of mass 2.3.2 Bernoulli Equation-conservation of energy 2.3.3 Equation of momentum-conservation of momentum 20 Homepage List Upwards Downwards Retumn Exit
Chapter 2 Fundamental Hydraulic Fluid Mechanics 20 2.3 Hydrodynamics 2.3.1 Equation of continuity—conservation of mass 2.3.2 Bernoulli Equation —conservation of energy 2.3.3 Equation of momentum—conservation of momentum