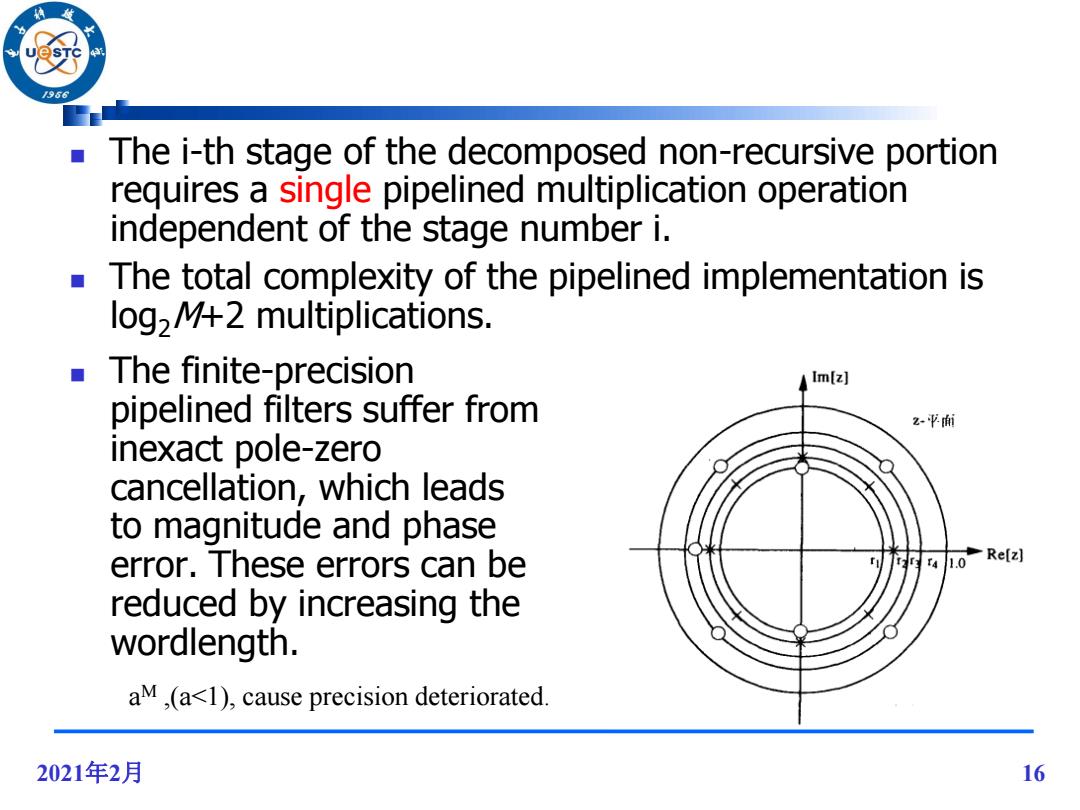
/96 The i-th stage of the decomposed non-recursive portion requires a single pipelined multiplication operation independent of the stage number i. ■ The total complexity of the pipelined implementation is log2M+2 multiplications. The finite-precision Im[z] pipelined filters suffer from 么平而 inexact pole-zero cancellation,which leads to magnitude and phase error.These errors can be r2r3 T4 1.0 Re[z reduced by increasing the wordlength. aM,(a<1),cause precision deteriorated. 2021年2月 16
2021年2月 16 The i-th stage of the decomposed non-recursive portion requires a single pipelined multiplication operation independent of the stage number i. The total complexity of the pipelined implementation is log2M+2 multiplications. The finite-precision pipelined filters suffer from inexact pole-zero cancellation, which leads to magnitude and phase error. These errors can be reduced by increasing the wordlength. a M ,(a<1), cause precision deteriorated

10.3.3 Look-Ahead Pipelining with General Decomposition /96 The idea of decomposition can be extended to any arbitrary number of loop pipelining stages M.M件2n 0 If M=MM..M,then the non-recursive stages implement (M-1),M(M2-1),..,MM..M-1(Mp 1)zeros,respectively,totaling (M1)zeros. Example:Consider the 1st-order Im[z] H(2)= 1-az Re[zj a/1.0 2021年2月 17
2021年2月 17 10.3.3 Look-Ahead Pipelining with General Decomposition The idea of decomposition can be extended to any arbitrary number of loop pipelining stages M. M≠2n If M=M1M2 ..Mp , then the non-recursive stages implement (M1 -1), M1 (M2 -1),.., M1M2 ..Mp-1 (Mp - 1) zeros, respectively, totaling (M-1) zeros. Example: Consider the 1st-order IIR 1 1 1 ( ) az H z