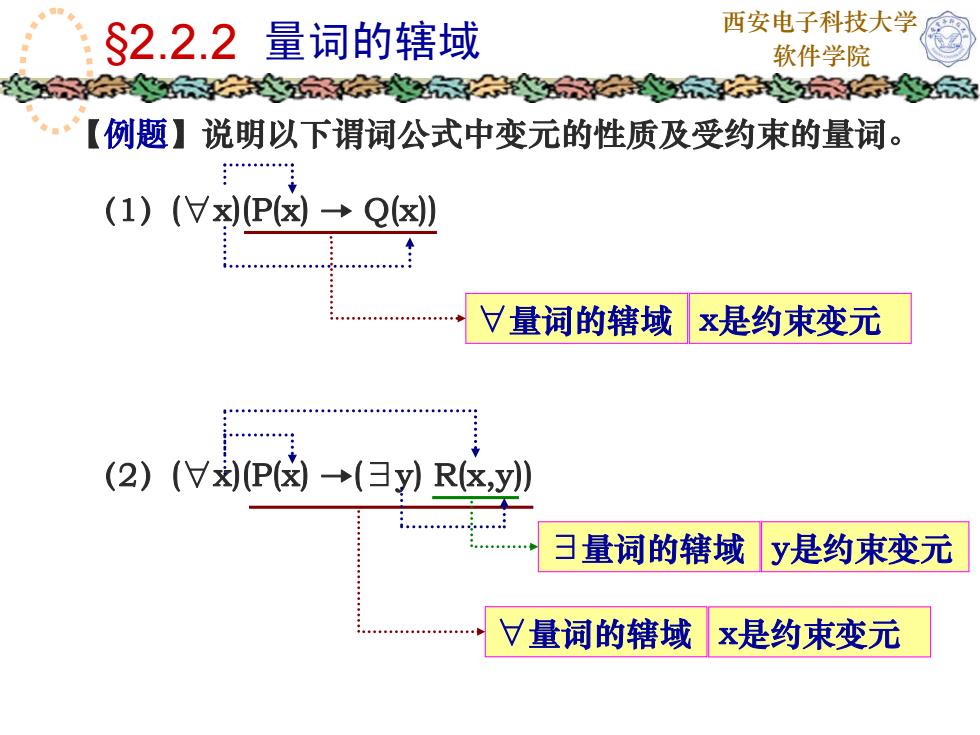
西安电子科技大学S2.2.2量词的辖域软件学院【例题】说明以下谓词公式中变元的性质及受约束的量词。(1) (Vx)(P(β) → Q(×)√量词的辖域x是约束变元(2) (V)(P(β) →(三y) R(x,y)日量词的辖域y是约束变元量词的辖域x是约束变元
西安电子科技大学 §2.2.2 量词的辖域 软件学院 【例题】说明以下谓词公式中变元的性质及受约束的量词。 (1)(∀x)(P(x) → Q(x)) (2)(∀x)(P(x) →(∃y) R(x,y)) ∀量词的辖域 x是约束变元 ∀量词的辖域 ∃量词的辖域 y是约束变元 x是约束变元

西安电子科技大学S2.2.2量词的辖域软件学院【例题】说明以下谓词公式中变元的性质及受约束的量词。(3) (Vx)(Vy)(P(x,y) VQ(y,z) ^ (日y) R(x,y)如果一个变元落入多个量词的辖域内,那么该变元被最靠近它的量词约束。(4) (V×)(P(β) ^(日y) R(x,y) VQ(x,y)两个同名的变元在同一个谓词公式中可以同时以约束变元和自由变元两种形式出现,但它们被认为是不同的个体变元
西安电子科技大学 §2.2.2 量词的辖域 软件学院 【例题】说明以下谓词公式中变元的性质及受约束的量词。 (3)(∀x)(∀y)(P(x,y)∨Q(y,z)∧(∃y) R(x,y)) (4)(∀x)(P(x)∧(∃y) R(x,y)) ∨Q(x,y) 如果一个变元落入多个量词的辖域内,那么该 变元被最靠近它的量词约束。 两个同名的变元在同一个谓词公式中可以同时 以约束变元和自由变元两种形式出现,但它们 被认为是不同的个体变元