
16-4设有一平面简谐波 y=0.02cos2叫00103 x,y以m计,t以s计, (1)求振幅、波长、频率和波速; (2)求x=0.1m处质点振动的初相位。 结束目录
16-4 设有一平面简谐波 x, y 以m计, t 以s计, (1)求振幅、波长、频率和波速; (2)求x = 0.1m处质点振动的初相位。 0.02 2π t y = cos x 0.01 0.3 结束 目录

解: y=0.02cos200103 y=0.02cos2(7-光)+9 两式比较得到: (1))A=0.02m v=100Hz九=0.3m u=入v=0.3×100=30m/s (2)当x=0.1m t=0一0=-2 结束 目录
0.02 2π t y = cos x 0.01 0.3 l 0.02 2π( )+ j t y = cos x T n =100Hz l =0.3m u= ln =0.3×100=30 m/s (1) A =0.02m t =0 = j 2π 3 解: 两式比较得到: (2) 当 x =0.1m 结束 目录

16-5一平面简谐纵波沿线圈弹簧传播, 设波沿着x轴正向传播,弹簧中某圈的最大 位移为3.0cm,振动频率为2.5Hz,弹簧中 相邻两疏部中心的距离为24cm。当t=0时, 在x=0处质元的位移为零并向x轴正向运动。 试写出该波的波动表式。 结束目录
16-5 一平面简谐纵波沿线圈弹簧传播, 设波沿着x 轴正向传播,弹簧中某圈的最大 位移为3.0cm,振动频率为2.5Hz,弹簧中 相邻两疏部中心的距离为24cm。当 t =0时, 在x =0处质元的位移为零并向x 轴正向运动。 试写出该波的波动表式。 结束 目录
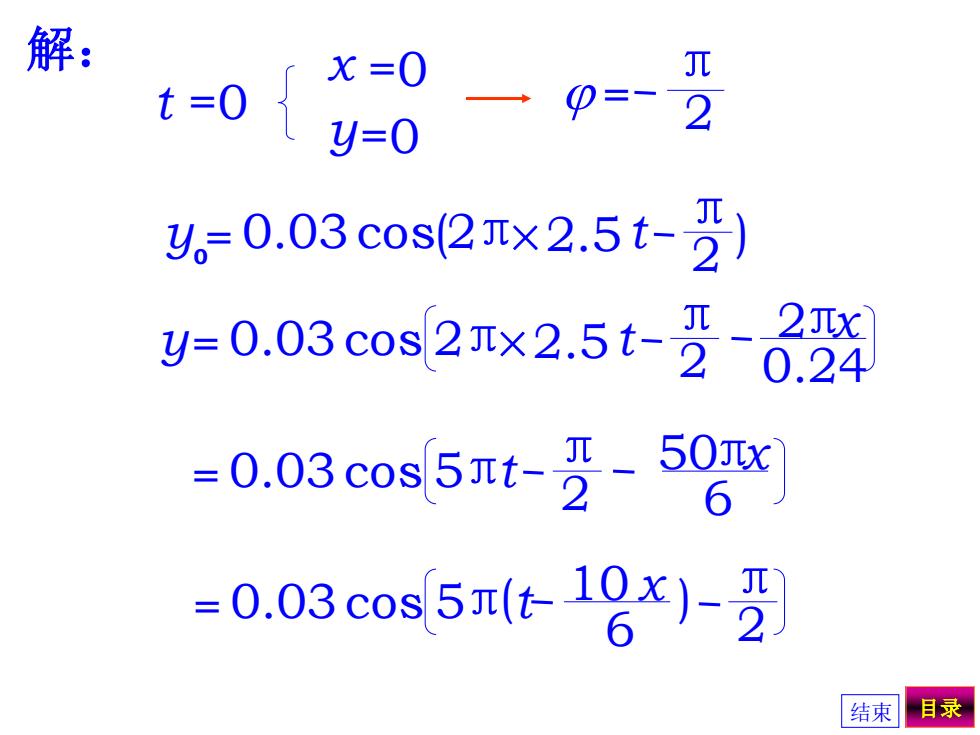
解: X=0 兀 t=0 y=0 0=-2 4.0.03c0s2x2.5t-2) y=0.03cos2x2.5t-32 =0.03cos5mt-2-50gx =0.03cos5t19x)-罗 结束目录
x =0 t =0 y = 0.03cos(2π t π) 2 0 ×2.5 y= 0.03cos 2π t π 2 ×2.5 2πx 0.24 = 0.03cos 5πt π 2 50πx 6 = 0.03cos 5πt π 2 10 x 6 ( ) y=0 π 2 j = 解: 结束 目录

16-6一平面简谐波沿x轴正向传播, 振幅A=0.1m,频率y=10Hz,当t=1.0s时 x=0.1m处的质点a的振动状态为: Va- dt Ja 此时x=20cm处的质点b的振动状态为 yp=5.0cm dy >0 Ub=dt b 求波的表式。 结束目录
16-6 一平面简谐波沿x 轴正向传播, 振幅 A =0.lm,频率n =l0Hz,当t =1.0s时 x =0.1m处的质点a的振动状态为: 此时x =20cm处的质点 b 的振动状态为 求波的表式。 yb = 5.0cm 0 dy dt b vb = > ya = 0 < 0 dy dt a va= 结束 目录