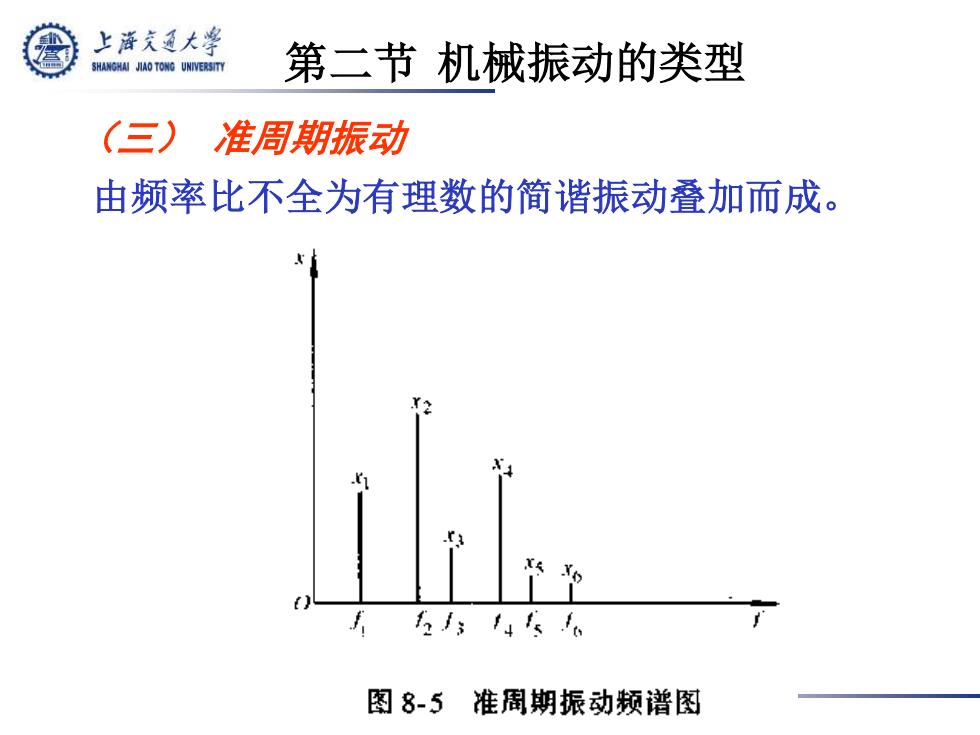
上海充通大学 SHANGHAI JIAO TONG UNIVERSITY 第二节机械振动的类型 (三)准周期振动 由频率比不全为有理数的简谐振动叠加而成。 2f:4 图8-5准周期振动频谱图
(三) 准周期振动 由频率比不全为有理数的简谐振动叠加而成。 第二节 机械振动的类型

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY 第二节机械振动的类型 (四) 瞬态振动、冲击 瞬态振动:在极短时间内仅持续几个周期的振动。 冲击是单个脉冲。 特点: >过程突然发生,持续时间短,能量很大。 >通常由零到无限大的所有频率的谐波分量构成
(四) 瞬态振动、冲击 ◼ 瞬态振动:在极短时间内仅持续几个周期的振动。 ◼ 冲击是单个脉冲。 ◼ 特点: ➢过程突然发生,持续时间短,能量很大。 ➢通常由零到无限大的所有频率的谐波分量构成。 第二节 机械振动的类型
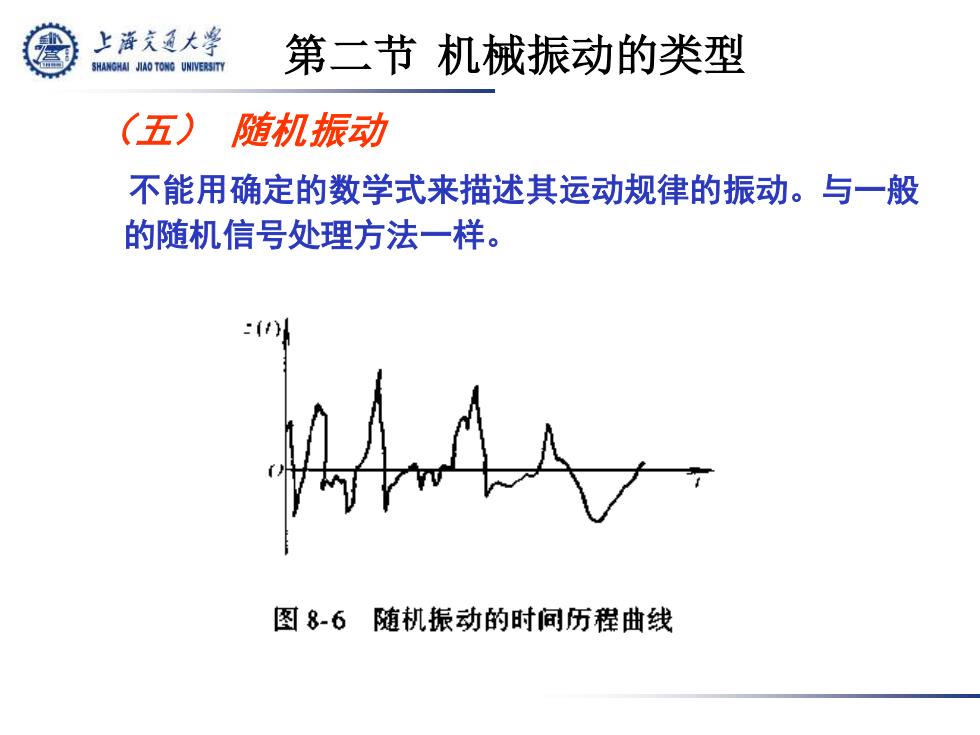
上海充通大学 SHANGHAI JIAO TONG UNIVERSITY 第二节机械振动的类型 (五)随机振动 不能用确定的数学式来描述其运动规律的振动。与一般 的随机信号处理方法一样。 图8-6随机振动的时间历程曲线
(五) 随机振动 不能用确定的数学式来描述其运动规律的振动。与一般 的随机信号处理方法一样。 第二节 机械振动的类型
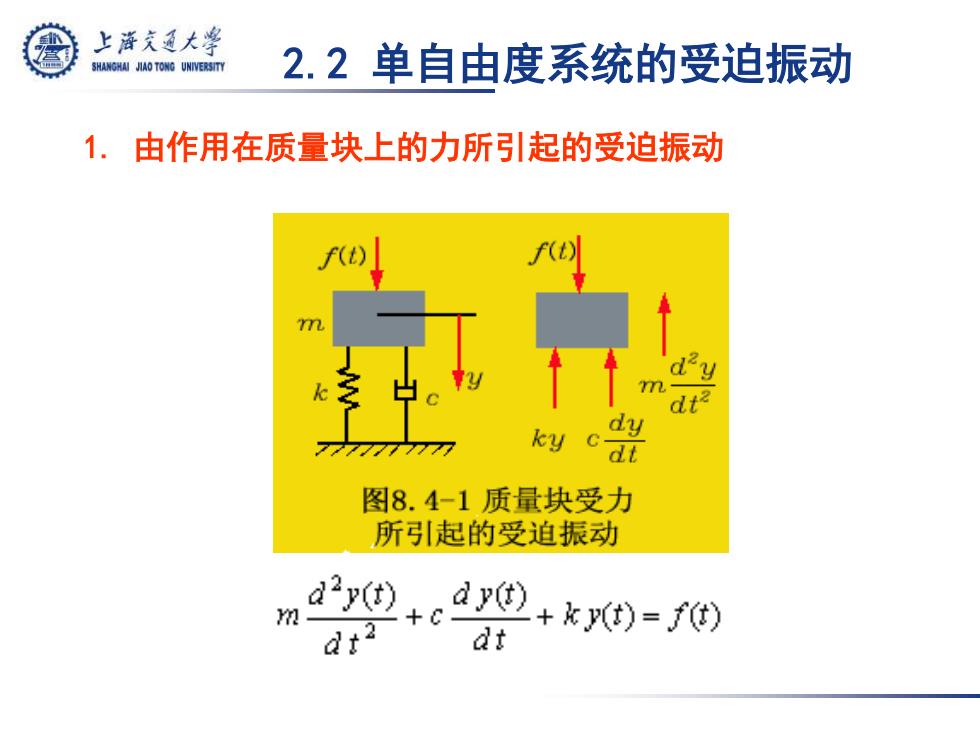
上泽充通大学 SHANGHAI JIAO TONG UNIVERSITY 2.2单自由度系统的受迫振动 1.由作用在质量块上的力所引起的受迫振动 ky c- dt 图8.4-1质量块受力 所引起的受迫振动 d"y()cdy()+ky(t)-f() dt2 dt
2.2 单自由度系统的受迫振动 1. 由作用在质量块上的力所引起的受迫振动

上海充通大学 SHANGHAI JIAO TONG UNIVERSITY 外加作用力:f(t)=F。sin(ot-a) Y,为质量块上作用有静力F时的静位移 Y=F。/k m 2√mk 稳态振动方程: y(t)=Ysin(ot-a-o)
0 2 2 2 2 0 ( ) sin( ) 2 sin( ) n n n f t F t d y dy y Y t dt dt = − + + = − 外加作用力: 0 0 , 2 Y F c mk = 0 0 n 为质量块上作用有静力 时的静位移 Y =F /k k = m y(t)=Ysin( t- 稳态振动方程 - : )