西安电子科技大学：《微波技术与天线》课程教学资源（课件讲稿）第一章 传输线理论（9/9）

2、圆波导 波导截面为圆形的波导称为圆波导。它具有损耗较小 和双极化的特性，常用于天线馈线中，也可作较远距离的传输 线，并广泛用作微波谐振腔。 圆波导的分析方法与矩形波导相似。首先求解纵向场 分量E(或H)的波动方程，求出E,(或H)的通解，并根据边界条 件求出它的特解，然后利用横向场与纵向场的关系式，求得所 有场分量的表达式，最后根据表达式讨论它的截止特性、传 输特性和场结构。 p=0 STE A.J.YUE 西安电子科技大学通信工程学院

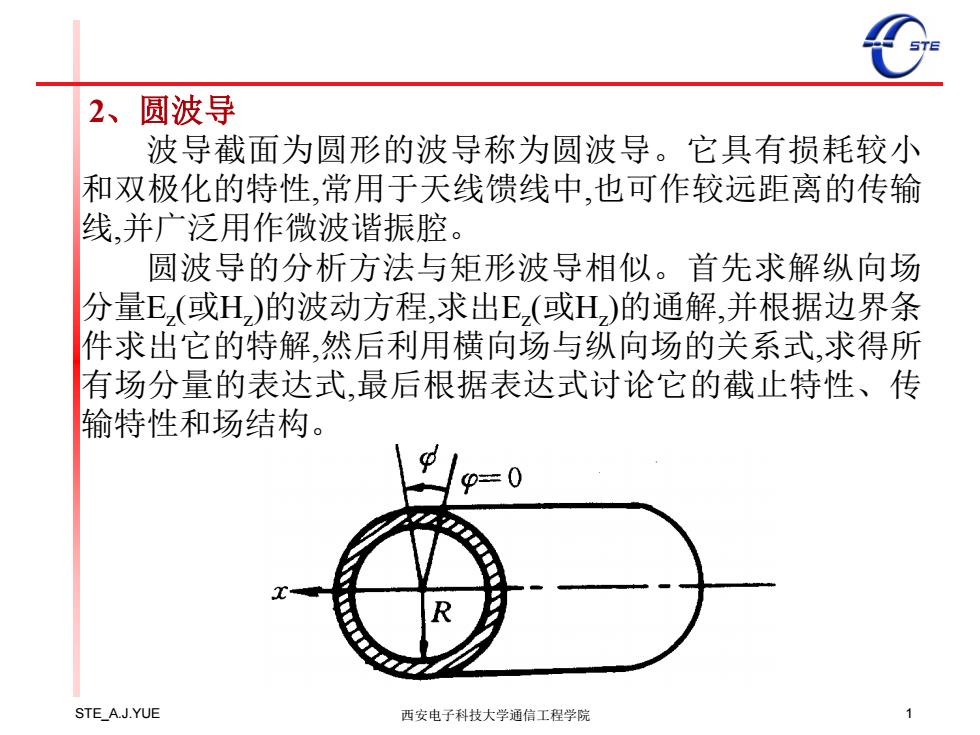
STE_A.J.YUE 西安电子科技大学通信工程学院 1 2、圆波导 波导截面为圆形的波导称为圆波导。它具有损耗较小 和双极化的特性,常用于天线馈线中,也可作较远距离的传输 线,并广泛用作微波谐振腔。 圆波导的分析方法与矩形波导相似。首先求解纵向场 分量Ez (或Hz )的波动方程,求出Ez (或Hz )的通解,并根据边界条 件求出它的特解,然后利用横向场与纵向场的关系式,求得所 有场分量的表达式,最后根据表达式讨论它的截止特性、传 输特性和场结构

DAT TE,MODE CIRCULAR WAVEGUIDE SHEL PRODUCTS AND CAPABILITIES No.B36C mec 2of2 C80-L c10 Sraight Section Fixed Termination C80-LS Sliding Termination 30-C Transition. C280-SC Circular to Rectangula Short Circuits Waveguide 03/85/8 D地ct te changeih加k+ STE_A.J.YUE 西安电子科技大学通信工程学院 2

STE_A.J.YUE 西安电子科技大学通信工程学院 2

(1)圆波导中TM、TE波场方程 对圆波导来说，h=1,h2=r代入式(1-28)就可得到柱 坐标系中所有横向场分量与纵向场分量的关系： OE. ay -Y 0 0 -j可u 1 0E E 1 0 -Y j而u 0 y or 居 0 j而8 -Y 0 oH. Ho 0 0 ap 1 aH. ∂p STE A.J.YUE 西安电子科技大学通信工程学院 3

STE_A.J.YUE 西安电子科技大学通信工程学院 3 （1）圆波导中TM、TE波场方程 对圆波导来说，h1=1,h2=r代入式（1-28）就可得到柱 坐标系中所有横向场分量与纵向场分量的关系： 2 0 0 1 1 0 0 0 0 0 0 1 z z c z z E E j E E j H k j H H j H                                                                               

(1)圆波导中TM、TE波场方程 此时E、H所满足的是柱坐标系下的二维亥姆霍兹方程式。在 给定边界条件下，F、H的解可用第一类贝塞尔函数Jm(x)表示成： E:EoJm(kcr) cosmo sinmp H:=HoJm (ker) cosmo sinmp c由边界条件决定。 对于TM波，其边界条件为：E-a=0即Jm(k.a)0, 对于TE波，其边界条件为：E。l,=a=0即Jm(ka小=0， 设4m是m阶贝塞尔函数Jm(x)的n个根4m是m阶贝塞尔函数的 导数J'm(x)的第n个根，由Jm(4nm)=0及Jm(4)=0则可得： 2na 对于TM波 kca-umo Amn 对于TE波 kea=prm λc= 2πa Amt STE_A.J.YUE 西安电子科技大学通信工程学院 4

STE_A.J.YUE 西安电子科技大学通信工程学院 4 （1）圆波导中TM、TE波场方程 此时Ez、Hz所满足的是柱坐标系下的二维亥姆霍兹方程式。在 给定边界条件下， Ez、Hz的解可用第一类贝塞尔函数 Jm (x)表示成： 对于TM波，其边界条件为： 即Jm (kca)=0， 对于TE波，其边界条件为： 即J'm (kca)=0， 设mn是 m阶贝塞尔函数Jm (x)的n个根， 是m阶贝塞尔函数的 导数 J’m (x)的第n个根，由 及 则可得： 对于TE波 对于TM波 E z a | 0    E  | 0 a  Jm mn ( ) 0   Jm mn   ( ) 0    mn  kc由边界条件决定

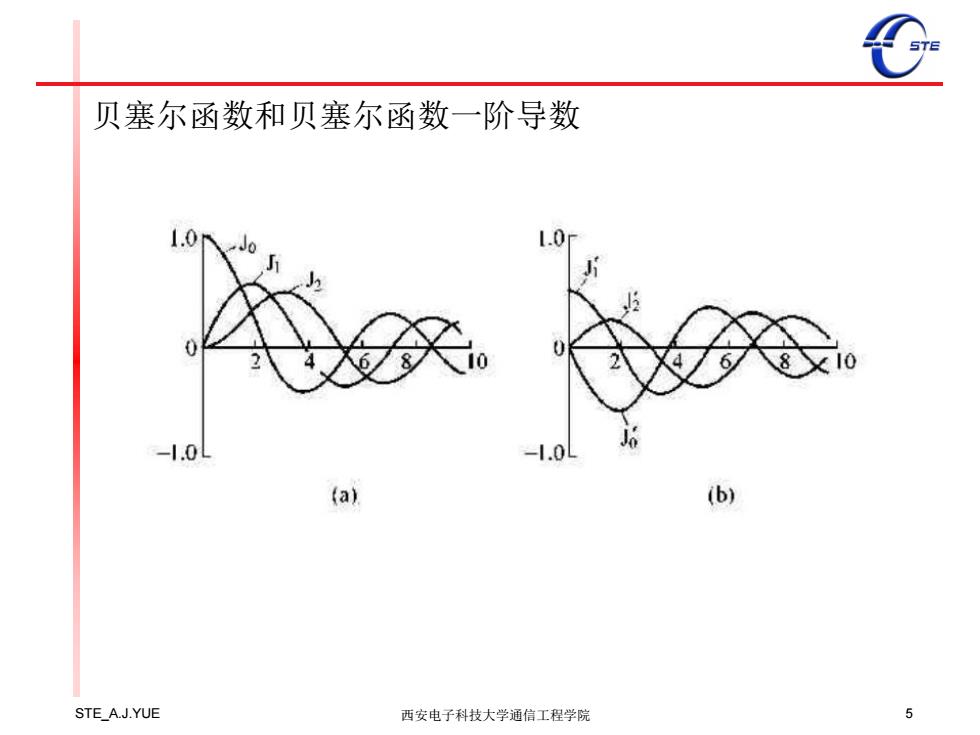
贝塞尔函数和贝塞尔函数一阶导数 1.0 Jo 1.0 -.0 -1.0 (a) (b) STE A.J.YUE 西安电子科技大学通信工程学院 5

STE_A.J.YUE 西安电子科技大学通信工程学院 5 贝塞尔函数和贝塞尔函数一阶导数