2

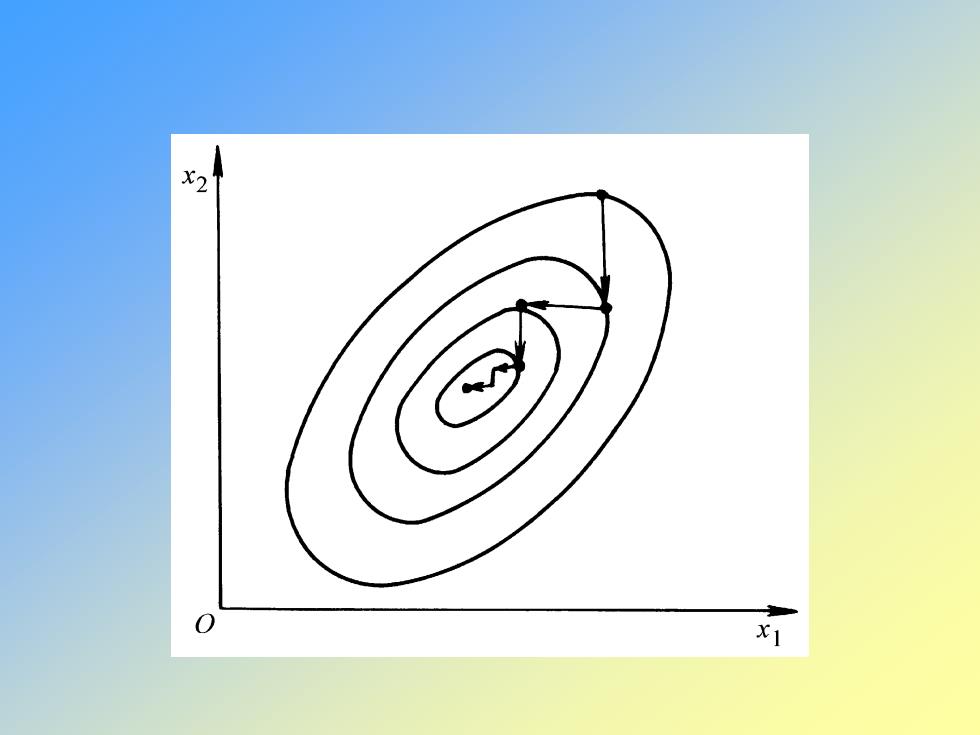
例4-1 求目标函数 ( ) 2 2 1 2 f x x x = + 25 的极小点
例4-1 求目标函数 ( ) 2 2 1 2 f x x x = + 25 的极小点

开始 给定x0、e k0 dk-vf (xk) xk+l←xk+adk k←k+1 ag:minf(xk+adk) 是 xk+1-xk<6? 否 x*←xk+l 结束

第三节牛顿型方法 在第三章中,我们已经讨论了一维搜索的牛顿方法。 得出一维情况下的牛顿迭代公式 ( ) ( ) 1 k k k k f x x x f x + = − 对于多元函数,在 k x 泰勒展开,得 f x x ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) 1 2 2 T T k k k k k k = + − + − − f x f x x x x x f x x x 设 k 1 x + 为函数的极小点,根据极值的必要条件
第三节牛顿型方法 在第三章中,我们已经讨论了一维搜索的牛顿方法。 得出一维情况下的牛顿迭代公式 ( ) ( ) 1 k k k k f x x x f x + = − 对于多元函数,在 k x 泰勒展开,得 f x x ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) 1 2 2 T T k k k k k k = + − + − − f x f x x x x x f x x x 设 k 1 x + 为函数的极小点,根据极值的必要条件

( ) 1 0 k x + = ( ) ( )( ) 2 1 0 k k k k f x f x x x + + − = ( ) ( ) 1 k k k k 1 2 x x f x f x − + = − 这是多元函数求极值的牛顿法迭代公式。 例4-2 用牛顿法求 ( ) 2 2 1 2 f x x x = + 25 的极小值。 对牛顿法进行改进,提出“阻尼牛顿法” ( ) ( ) 1 k k k k 1 2 k x x f x f x − + = − ( ) 1 min k k k k k k f x f x a d f x ad + = + = +
( ) 1 0 k x + = ( ) ( )( ) 2 1 0 k k k k f x f x x x + + − = ( ) ( ) 1 k k k k 1 2 x x f x f x − + = − 这是多元函数求极值的牛顿法迭代公式。 例4-2 用牛顿法求 ( ) 2 2 1 2 f x x x = + 25 的极小值。 对牛顿法进行改进,提出“阻尼牛顿法” ( ) ( ) 1 k k k k 1 2 k x x f x f x − + = − ( ) 1 min k k k k k k f x f x a d f x ad + = + = +