
第六章 约束优化方法 根据求解方式的不同,可分为直接解法和间接解法 两类。 1, 2,., 1, 2,., u m v p n = = ( ) 0 ( ) 0 u v g x h x = min f x( ) n x R st. . 机械优化设计的问题,大多属于约束优化设计问题, 其数学模型为: 直接解法是在满足不等式约束的可行设计区域内直接求 出问题的约束最优解。 属于这类方法的有:随机实验法、随机方向搜索法、 复合形法、可行方向法等
第六章 约束优化方法 根据求解方式的不同,可分为直接解法和间接解法 两类。 1, 2,., 1, 2,., u m v p n = = ( ) 0 ( ) 0 u v g x h x = min f x( ) n x R st. . 机械优化设计的问题,大多属于约束优化设计问题, 其数学模型为: 直接解法是在满足不等式约束的可行设计区域内直接求 出问题的约束最优解。 属于这类方法的有:随机实验法、随机方向搜索法、 复合形法、可行方向法等

间接解法是将约束优化问题转化为一系列无约束优化问题来 解的一种方法。 由于间接解法可以选用已研究比较成熟的无约束优化方法, 并且容易处理同时具有不等式约束和等式约束的问题。因而 在机械优化设计得到广泛的应用。 间接解法中具有代表性的是惩罚函数法。 直接解法的基本思想: 在由m个不等式约束条件gu (x)≤0所确定的可行域φ内,选 择一个初始点x (0),然后确定一个可行搜索方向S,且以适当 的步长沿S方向进行搜索,取得一个目标函数有所改善的可 行的新点x (1),即完成了一次迭代。以新点为起始点重复上 述搜索过程,每次均按如下的基本迭代格式进行计算:
间接解法是将约束优化问题转化为一系列无约束优化问题来 解的一种方法。 由于间接解法可以选用已研究比较成熟的无约束优化方法, 并且容易处理同时具有不等式约束和等式约束的问题。因而 在机械优化设计得到广泛的应用。 间接解法中具有代表性的是惩罚函数法。 直接解法的基本思想: 在由m个不等式约束条件gu (x)≤0所确定的可行域φ内,选 择一个初始点x (0),然后确定一个可行搜索方向S,且以适当 的步长沿S方向进行搜索,取得一个目标函数有所改善的可 行的新点x (1),即完成了一次迭代。以新点为起始点重复上 述搜索过程,每次均按如下的基本迭代格式进行计算:
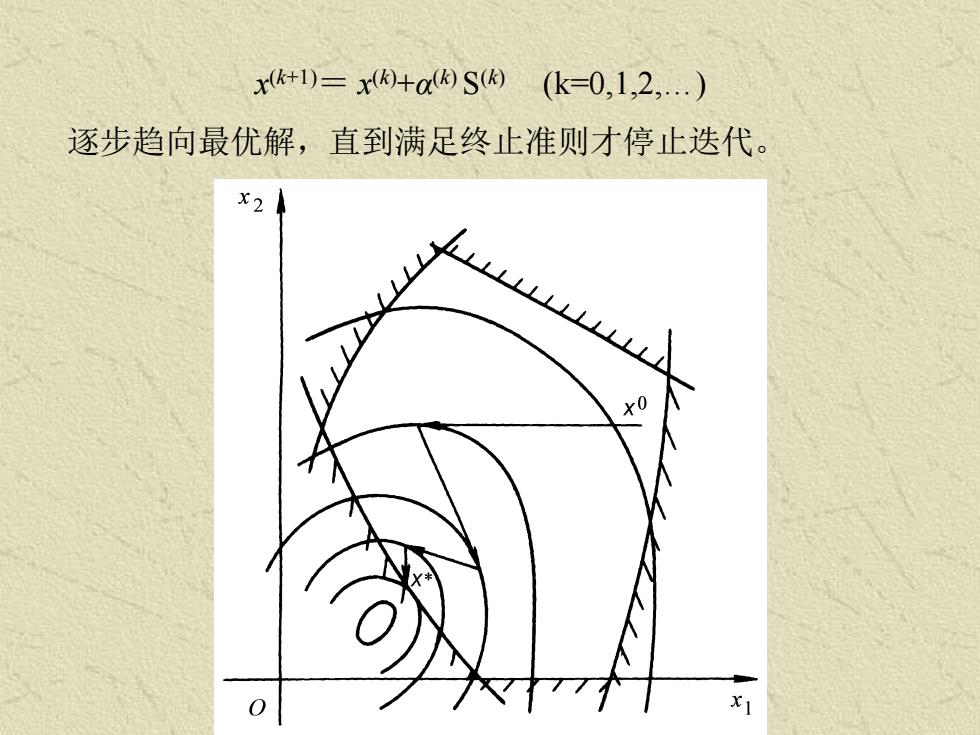
x (k+1)= x (k)+α (k) S (k) (k=0,1,2,.) 逐步趋向最优解,直到满足终止准则才停止迭代
x (k+1)= x (k)+α (k) S (k) (k=0,1,2,.) 逐步趋向最优解,直到满足终止准则才停止迭代

直接解法的原理简单,方法实用,其特点是: 1)由于整个过程在可行域内进行,因此,迭代计算不论 何时终止,都可以获得比初始点好的设计点。 2)若目标函数为凸函数,可行域为凸集,则可获得全域 最优解,否则,可能存在多个局部最优解,当选择的初始 点不同,而搜索到不同的局部最优解。 3)要求可行域有界的非空集
直接解法的原理简单,方法实用,其特点是: 1)由于整个过程在可行域内进行,因此,迭代计算不论 何时终止,都可以获得比初始点好的设计点。 2)若目标函数为凸函数,可行域为凸集,则可获得全域 最优解,否则,可能存在多个局部最优解,当选择的初始 点不同,而搜索到不同的局部最优解。 3)要求可行域有界的非空集
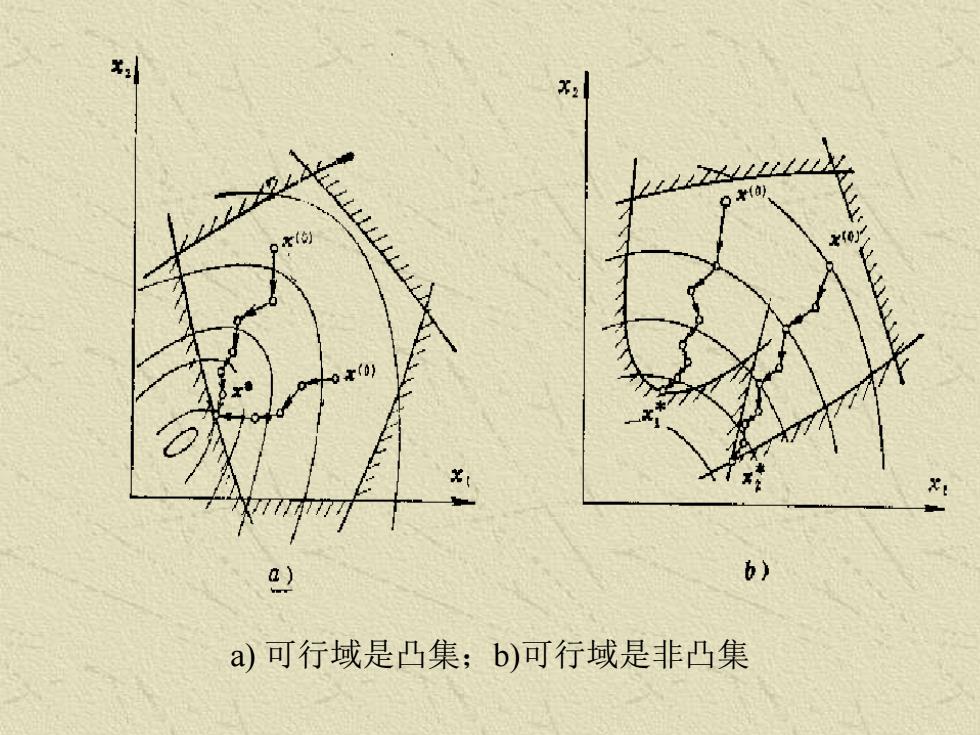
a) 可行域是凸集;b)可行域是非凸集
a) 可行域是凸集;b)可行域是非凸集