
第三章一维搜索方法 k k k 1 k x x a d + = + 采用数学规划法求函数极值点的迭代计算: K+1次迭代的搜索方向 搜索的最佳步长因子 当搜索方向 给定,求最佳步长 k a k d 就是求一元函数的极值。 ( ) ( ) ( ) k k k 1 k k f x f x a d a + = + = 称为一维搜索。 是优化搜索方法的基础。 求解一元函数 (a ) 的极小点 * a ,可用解析法
第三章一维搜索方法 k k k 1 k x x a d + = + 采用数学规划法求函数极值点的迭代计算: K+1次迭代的搜索方向 搜索的最佳步长因子 当搜索方向 给定,求最佳步长 k a k d 就是求一元函数的极值。 ( ) ( ) ( ) k k k 1 k k f x f x a d a + = + = 称为一维搜索。 是优化搜索方法的基础。 求解一元函数 (a ) 的极小点 * a ,可用解析法

( ) ( ) ( ) ( ) ( ) 1 2 T T f x ad f x ad f x ad G ad + + + 上式求α的极值,即求α导数为零。 ( ) ( ) 1 2 2 T T = + + f x d f x d Gd ( ) * 0 T T d f x d Gd + = 则 ( ) * T T d f x d Gd = − 从上式看,需要求导进行计算,对于函数关系复杂的, 解析法十分不便。 数值法的基本思路:确定 的搜索区间,在不断缩小 区间,最终获得近似值。 *
( ) ( ) ( ) ( ) ( ) 1 2 T T f x ad f x ad f x ad G ad + + + 上式求α的极值,即求α导数为零。 ( ) ( ) 1 2 2 T T = + + f x d f x d Gd ( ) * 0 T T d f x d Gd + = 则 ( ) * T T d f x d Gd = − 从上式看,需要求导进行计算,对于函数关系复杂的, 解析法十分不便。 数值法的基本思路:确定 的搜索区间,在不断缩小 区间,最终获得近似值。 *
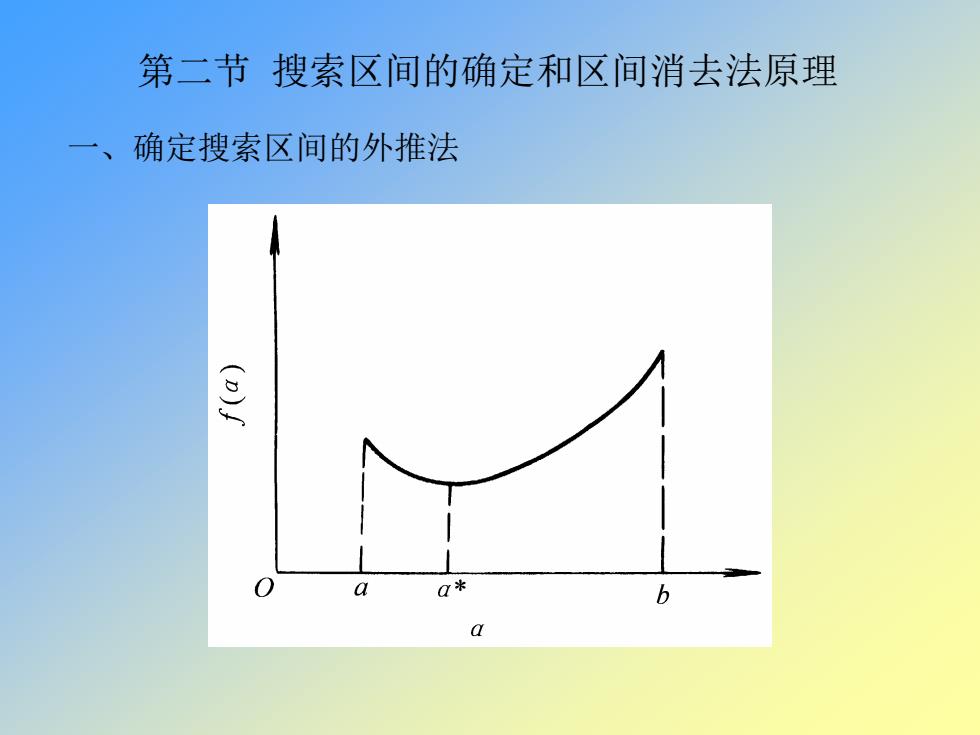
第二节 搜索区间的确定和区间消去法原理 一、确定搜索区间的外推法
第二节 搜索区间的确定和区间消去法原理 一、确定搜索区间的外推法
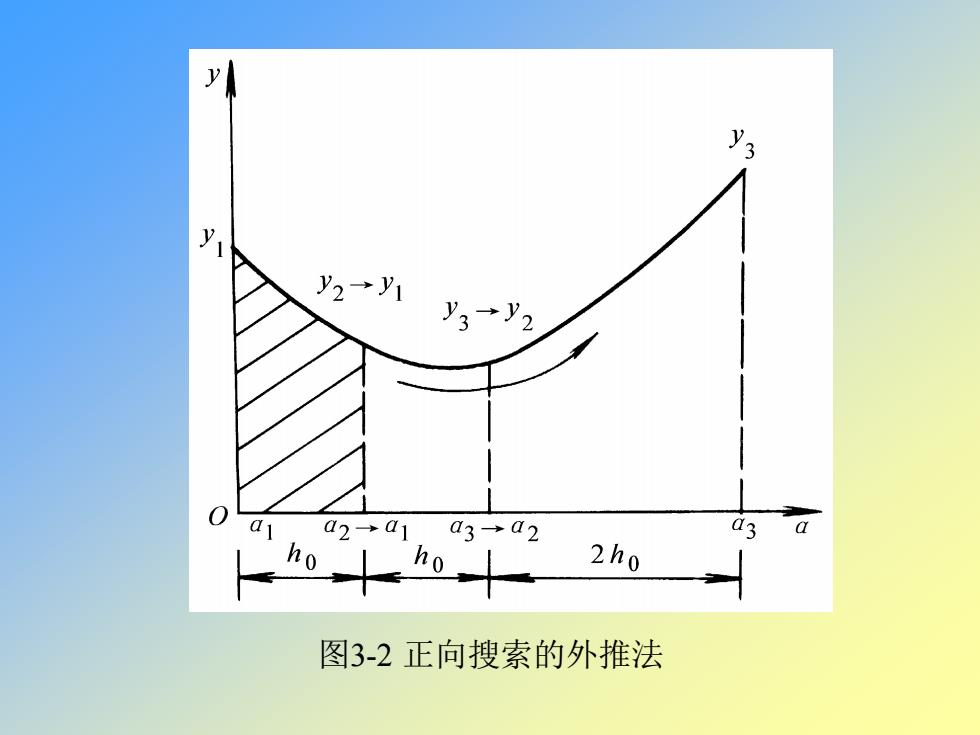
图3-2 正向搜索的外推法
图3-2 正向搜索的外推法
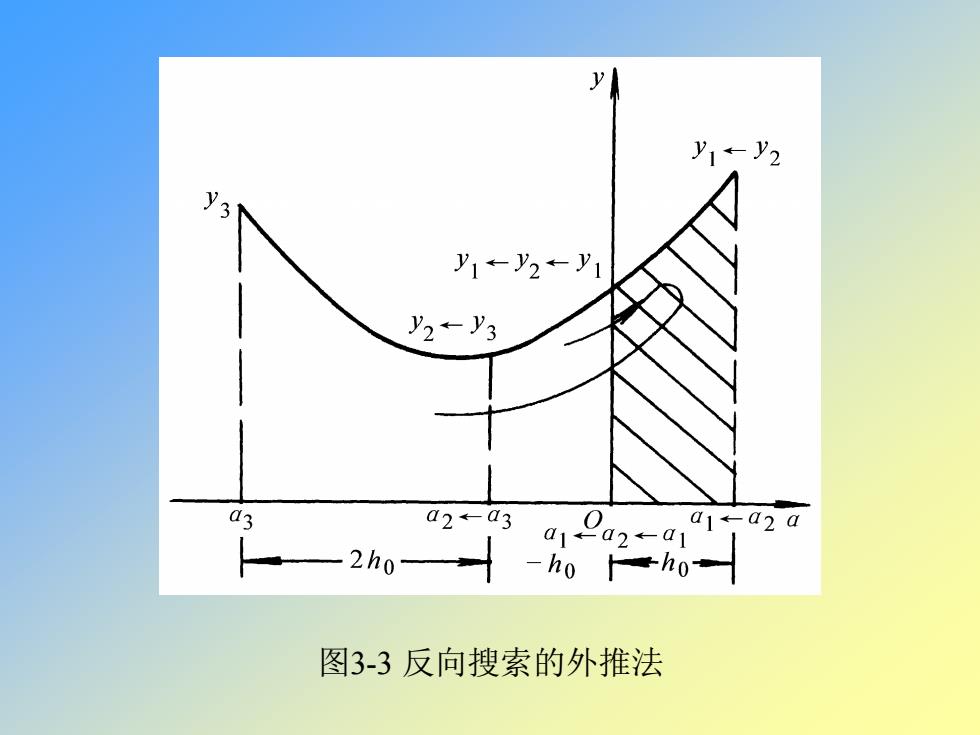
图3-3 反向搜索的外推法
图3-3 反向搜索的外推法