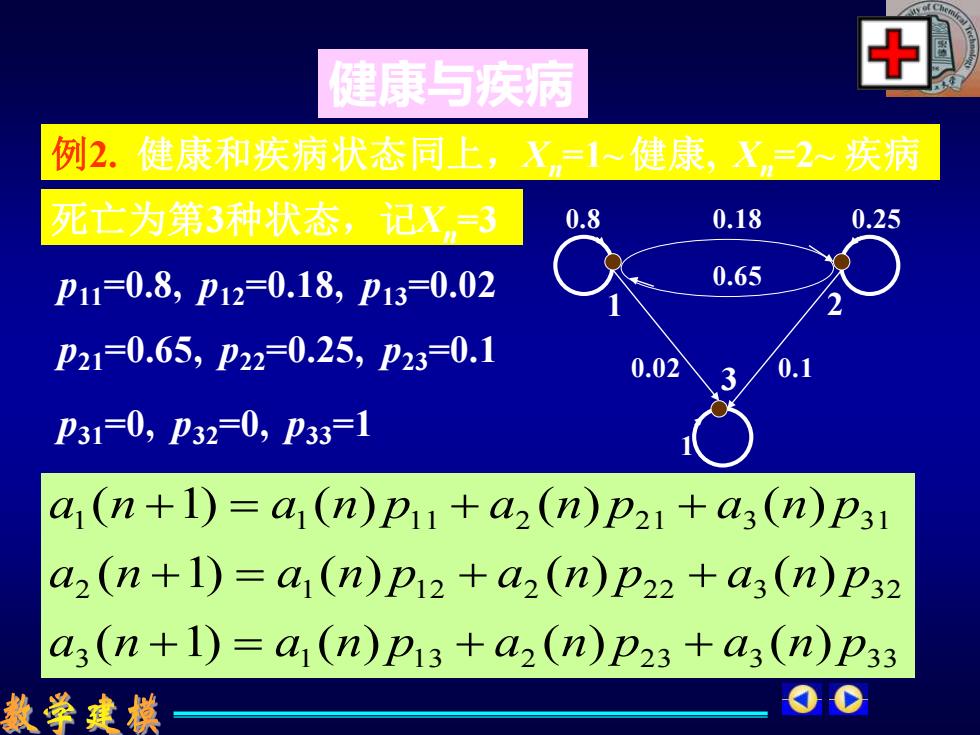
健康与疾病 例2.健康和疾病状态同上,X=1~健康,X=2疾病 死亡为第3种状态,记X=3 0.8 0.18 0.25 p11=0.8,p12=0.18,p13=0.02 0.65 P21=0.65,p22=0.25,p23=0.1 0.02 P31=0,p32=0,P33=1 a1(n+1)=a(n)p11+a2(n)p21+a3(n)p31 a2(n+1)=a,(n)p12+a2(n)p22+a3(n)p32 a3(n+1)=a1(n)p13+a2(n)p23+a3(n)p33 教学建摸
1 2 3 0.02 0.1 1 0.8 0.18 0.25 0.65 例2. 健康和疾病状态同上,Xn=1~ 健康, Xn=2~ 疾病 3 1 1 3 2 2 3 3 3 3 2 1 1 2 2 2 2 3 3 2 1 1 1 1 2 2 1 3 3 1 ( 1) ( ) ( ) ( ) ( 1) ( ) ( ) ( ) ( 1) ( ) ( ) ( ) a n a n p a n p a n p a n a n p a n p a n p a n a n p a n p a n p + = + + + = + + + = + + p11=0.8, p12=0.18, p13=0.02 死亡为第3种状态,记Xn=3 健康与疾病 p21=0.65, p22=0.25, p23=0.1 p31=0, p32=0, p33=1

状态与状态转移 中 设投保时处于健康状态,预测a(n),n=1,2. n 0 2 3 50 0 a(n) 1 0.8 0.7570.7285 0.1293 。。 0 42(n 0 0.180.189 0.1835.. 0.0326. 0 a;(n 0 0.020.0540.0880.. 0.8381. 不论初始状态如何,最终都要转到状态3; ·一旦a1k)=2)=0,3(k)=1,则对于>k,a1n=0, a2()=0,3(n=1,即从状态3不会转移到其它状态。 数学建模
n 0 1 2 3 a2 (n) 0 0.18 0.189 0.1835 a3 (n) 0 0.02 0.054 0.0880 a1 (n) 1 0.8 0.757 0.7285 设投保时处于健康状态,预测 a(n), n=1,2… • 不论初始状态如何,最终都要转到状态3 ; • 一旦a1 (k)= a2 (k)=0, a3 (k)=1, 则对于n>k, a1 (n)=0, a2 (n)=0, a3 (n)=1, 即从状态3不会转移到其它状态。 状态与状态转移 0 0 1 50 0.1293 0.0326 0.8381

马氏链的基本方程 伏存1=12,川=国 状态概字和=P(.Y,三) 7=12,k,1=0 转移概率p,=P(X1=jX,=) p,20,∑P,=li=12,…k 基本方程 a,(n+1)=∑a,(0p,i=1,2,…,k 1)=(a107).,a( a(n+1)=a(n)P 状态概率向冒 P=P,转移率矩陶 a(n)=a(0)P" 非负.行为 教学建模
1,2,, , 0,1, ( ) ( ), = = = = i k n a n P X i 状态概率 i n ( ) 1 p P X j X i 转移概率 ij = n+ = n = X =1,2, k (n = 0,1, ) 马氏链的基本方程 状态 n ( ) 1 1 = = a n k i i p p i k k j i j i j 0, 1, 1,2, , 1 = = = (非负,行和为 ) 转移概率矩阵 1 P ={pi j}kk ~ a(n +1) = a(n)P a n a n p i k k j i j j i ( 1) ( ) , 1,2, , 1 + = = = 基本方程 ~ 状态概率向量 ( ) ( ( ), ( ), , ( )) 1 2 a n a n a n a n = k n a(n) = a(0)P

马氏链的两个重要类型 a7+三m 1.正则链~从任一状态出发经有限次转移 能以正概率到达另外任一状态(如例1) E则链今3V,P'>0 正则链→3N,a(n)一→代n-→oo)w~稳态概率 w满足wP=W 08w,+0711 0.802 0024=0.7w 0.703 021,十031三1 w满足 w,=1 1m=7/92/9 i=l 数学纸保】
w满足 wP = w 马氏链的两个重要类型 1. 正则链 ~ 从任一状态出发经有限次转移 能以正概率到达另外任一状态(如例1)。 , 0 N 正则链 N P a(n +1) = a(n)P 正则链w, a(n) →w(n →) = 0.7 0.3 0.8 0.2 例1. P w = (7 / 9,2 / 9) 1 2 2 1 2 1 0.2 0.3 0.8 0.7 w w w w w w + = + = 1 1 = = k i w满足 wi 1 w1 +w2 = 1 2 0.2w = 0.7w w ~ 稳态概率

马氏链的两个重要类型 2 吸收链~存在吸收状态 (一旦到达就不会离 开的状态,P一),且从任一非吸收状态出发经有 限次转移能以正概率到达吸收状态(如例2) 有个吸收状态的吸收链 R有非 的转移概率阵标准形式 零元素 M=(1-)'=∑Q y=()=6 y~从第i个非吸收状态出发,被某个 吸收状态吸收前的平均转移次数。 教学建摸
= R Q I P r r 0 马氏链的两个重要类型 2. 吸收链 ~ 存在吸收状态(一旦到达就不会离 开的状态i, pii=1),且从任一非吸收状态出发经有 限次转移能以正概率到达吸收状态(如例2)。 有r个吸收状态的吸收链 的转移概率阵标准形式 R有非 零元素 = − = − = 0 1 ( ) s s M I Q Q T e = (1,1, ,1) y y y y Me = ( 1 , 2 , k−r ) = yi ~ 从第 i 个非吸收状态出发,被某个 吸收状态吸收前的平均转移次数